This site is being phased out.
Simplicial complexes and maps
Contents
From graphs to simplicial complexes
A graph is pure data. It consists of two sets:
- the nodes, say, $N=\{A, B, C, D\}$, representing some agents, and
- the edges, say, $E=\{AB, BC, CA, DA, CD\}$, representing some pairwise relation between them. $\\$
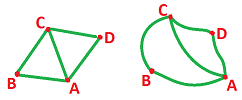
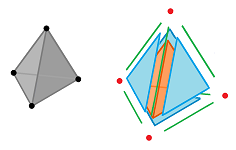
The topology is hidden in the data and, in order to see it, we often have to illustrate the data by a subset of the Euclidean space, as follows. Each node is plotted as a distinct point, but otherwise arbitrarily, and these points are connected by simple curves (paths) that can have only the nodes in common:
This set is called a realization of the graph, which is no more than an illustration of the data.
Now, with a graph on the left, what could be the meaning of the data behind the picture on the right?
There must be some new kind of relation present! This three-way relation exists for $A,B,C$ but not for $A,C,D$.
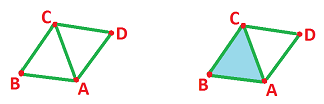
We now have a collection $K$ of three sets:
- the nodes $N=\{A, B, C, D\}$ representing some agents,
- the edges $E=\{AB, BC, CA, DA, CD\}$ representing some pairwise relations, and
- the triangular face(s) $F=\{ABC\}$ representing some three-way relations. $\\$
This data set is called a simplicial complex (or sometimes even a “multi-graph”). Its elements are called $0$-, $1$-, and $2$-simplices.
Example (graph). The graph $G$ above may come from a series of phone conversation between the four individuals: $$\begin{array}{c|cccccc} & A &B &C &D \\ \hline A: &- &+ &+ &+\\ B: &+ &- &+ &-\\ C: &+ &+ &- &+\\ D: &+ &- &+ &-. \end{array}$$ Here, the fact that a conversation has occurred, it is marked with “+” and visualized with an edge. $\square$
Example (simplicial complex). Meanwhile, the simplicial complex $K$ above may come from, say, the list of stores visited by these individuals: $$\begin{array}{c|cccccc} & K &M &J &W \\ \hline A: &+ &+ &+ &-\\ B: &+ &- &- &- \\ C: &+ &+ &- &+\\ D: &- &- &+ &+. \end{array}$$ Here, “K” may stand for Kroger (the triangle), “M” for Macy's, “J” for JCPenney, and “W” for Walmart (the edges). $\square$
Exercise. Create a similar table for yourself and four of your best friends documenting your joint activities. Create a simplicial complex.
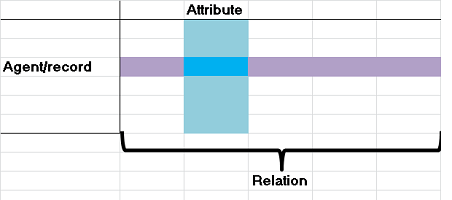
Example (database). A similar construction is possible for any “relational database”, which is simply a table:
For a single column table, every collection of $n$ agents that happen to have an identical attribute form an element of our simplicial complex, an $(n-1)$-simplex. $\square$
Definition. Suppose a (possibly infinite) set $S$ is given. A collection $K$ of subsets, called simplices, of $S$ is called a simplicial complex if (1) any subset of any simplex is also a simplex: $$\tau \in K, \sigma \subset \tau \Longrightarrow \sigma \in K,$$ and (2) every simplex is a subset of only finitely many simplices. If simplex $a$ has exactly $n+1$ elements, it is called an $n$-simplex, or simplex of dimension $n=\dim a$. The highest dimension of a simplex in $K$ is called the dimension of $K$: $$\dim K:= \displaystyle \max _{a\in K} \dim a.$$
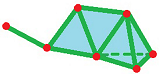
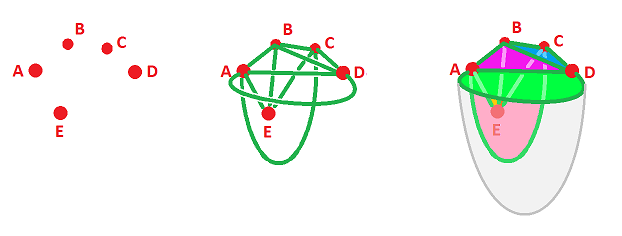
Here is an example of a “realization” of a $2$-dimensional simplicial complex as a metric complex in ${\bf R}^3$:
And here is a complex that may seem to contain only one $3$-simplex, blown up:
Example. A realization of the complex $$K=\{ABD, BCD, ACD, ABE, BCE, ACE\}$$ is found by gluing these $6$ “triangles” to each other. Or we can start by listing the lower-dimensional cells:
- $0: \{A,B,C,D,E\}$,
- $1: \{AB,BD, AD,BC,CD,AE,BE,AC,CE\}$. $\\$
Then we build a realizaiton of $K$ dimension by dimension:
We throw the vertices (the singletons from $K$) around in ${\bf R}^3$ and then connect them by the paths (the pairs in $K$) trying to keep them unknotted for simplicity. Finally, we add the faces (the triples in $K$) as pieces of fabric stretched on these wire-frames.
The result is homeomorphic to the sphere. $\square$
Exercise. (a) Demonstrate that a relational database with a single attribute produces a simplicial complex as described above. (b) Give an example how simplices (and a simplicial complex) can be formed without requiring the attributes to be identical. (c) How is a complex formed if there are more than one attribute?
Boundaries of simplices
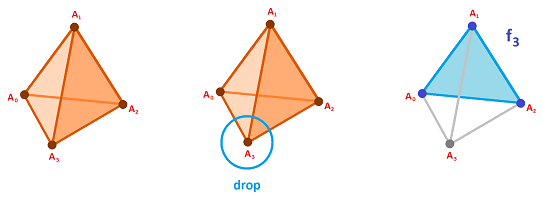
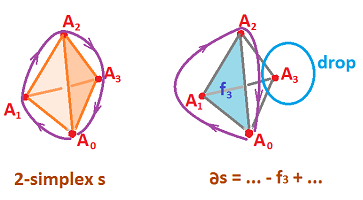
The boundary of a $n$-simplex is made of its $(n-1)$-faces. Those are easy to construct by choosing one vertex at a time and considering the opposite face:
As a data structure, the $n$-simplex is just a list of $n+1$ items called vertices: $$s = A_0A_1 ... A_n,$$ and any of its $(n-1)$-faces is the same list with one item dropped (indicated by the brackets): $$\begin{array}{ll} f_0 &= [A_0]A_1 ... A_n,\\ f_1 &= A_0[A_1] ... A_n,\\ &...\\ f_n &= A_0A_1 ... [A_n]. \end{array}$$ Such a simple construction doesn't exist for cubes. Instead, we relied on their product structure to prove our theorems.
In the unoriented case, a chain is, as before, defined as a “combination” of cells, i.e., a formal, binary sum of cells. In the last example, there are only these $1$-chains: $$0,\ a,\ b,\ c,\ a + b,\ b + c,\ c + a,\ a + b + c. $$
It is clear now that the boundary of an $n$-simplex is the sum of its $(n-1)$-faces. It's an $(n-1)$-chain: $$\partial _n s:= \displaystyle\sum_{i=0}^n f_i = \displaystyle\sum_{i=0}^n A_0 ... A_{i-1}[A_i]A_{i+1}...A_n.$$
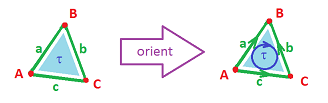
How to orient a simplex
The first step in developing the homology over the reals is to add more structure to the complex -- orientation of cells.
Recall that for cubical complexes we initially defined the orientation for $1$-cells only as their directions. It can be arbitrary or it can be aligned with the axes:
These directions, however, don't suggest any particular way of orienting the squares. Instead, it is defined as clockwise or counterclockwise orderings of the vertices. This approach, however, proved itself too complex for higher dimensions and we instead relied on the representation of each cube as a product of edges and vertices.
Defining such orientation is also possible based the geometry of the Euclidean space; for example, a plane (and a square) in the $3$-dimensional space is oriented by a choice of one of the two unit normal vectors.
Exercise. Show that this is the choice between two equivalence classes of normal vectors.
The idea extends to subspaces of dimension $n-1$ in ${\bf R}^n$. Regrettably, this “external” approach to orientation fails when the dimension of the subspace is less than $n-1$ because the normal vectors don't split into two equivalence classes anymore.
The most important thing we know is that
Following our treatment of cubical complexes, we first define the directions of all edges of our simplicial complex and, this time, the direction of an edge isn't dictated by the ambient space (there is none) -- the choice is entirely ours!
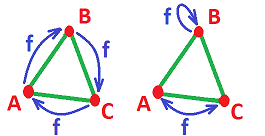
We illustrate this idea below. In this simplicial complex representation (triangulation) of the circle, all three edges have been oriented, at random:
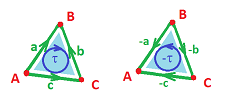
Here, the $1$-simplices aren't just edges $a, b, c$ but $$a = AB =- BA,\ b = CB =- BC,\ c = AC =-CA.$$ We could have chosen any other order of vertices: $a = BA, b = CB, c = CA$, etc.
Early on, let's make it clear that another choice of cells' orientations will produce different but isomorphic groups of chains. In fact, choosing an orientation of a complex is just a special case of choosing a basis of a vector space.
Next, after using directions to define orientation of edges, how do we handle orientations of higher-dimensional simplices?
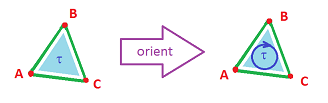
As there is no such thing as “the direction of a triangle”, we need to think of something else. Looking at the picture below, the answer seems obvious: we go around it either clockwise or counterclockwise:
Unfortunately, this idea has no analog for a $3$-simplex. There is no such thing as a “clockwise path” in a cube. In fact, there is no circular path through all of its vertices that capture all possible orderings.
Exercise. Prove the last statement. Hint: just count.
We find the answer in the definition of simplicial complex: it relies only on the data structure and so should the definition of orientation.
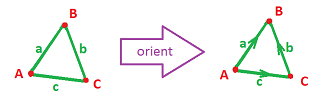
First, let's observe that speaking of edge $AB$ being an element of complex $K$ is misleading because the elements of $K$ are subsets of set $S$. Therefore, to be precise we wouldn't write: $$AB \in K,$$ until the orientation has been already introduced, but instead: $$\{A,B\}\in K.$$ Considering the fact that these are equal, $\{A,B\}=\{B,A\}$, as sets, here's our conclusion: choosing $AB$ over $BA$ is equivalent to choosing an ordering of the set $\{A,B\}$.
So, the idea is that an orientation of a simplex is simply a specific choice of order of its vertices.
Let's consider the triangle. For a $2$-simplex with vertices $A,B,C$, we have $6$ possible orderings of the vertices:
- $ABC$, $BCA$, and $CAB$ for clockwise, and
- $ACB$, $CBA$, and $BAC$ for counter-clockwise. $\\$
But there should be only two orientations! It follows then that an orientation should be a choice of one of these two classes of orderings. What are they exactly? They are simply “reorderings” of $ABC$, i.e., self-bijections of $\{A,B,C\}$. We recognize them as permutations.
Recall, an even/odd permutation is the composition of an even/odd number of transpositions, elementary permutations that “flips” exactly two elements. For example,
- it takes two flips to get $CAB$ from $ABC$, so it's even; but
- it takes one flip to get $ACB$ from $ABC$, so it's odd. $\\$
We know that the even permutations form the subgroup $\mathcal{A}_n$ of the symmetric group $\mathcal{S}_n$ of all permutations of a set of $n$ elements.
Exercise. Prove the above statement.
Exercise. A permutation $\sigma\in\mathcal{S}_n$ of the basis vectors of ${\bf R}^{n}$ defines a linear operator. What can you say about its determinant? What about $\sigma\in\mathcal{A}_n$?
So, the definition of orientation of simplices is based on the fact that there are two equivalence classes of orderings of any set and, in particular, on the set of vertices of a simplex:
Of course, these two classes are the two cosets that form the following quotient group: $$\mathcal{S}_n / \mathcal{A}_n \cong {\bf Z}_2.$$
Definition. Suppose an $n$-simplex $\tau$ is given as an ordered list of $n+1$ elements, $\tau=A_0A_1...A_n.$ Then we say that $\tau$ is an oriented simplex if either the class of even permutations of the vertices $\{A_0,A_1, ...,A_n\}$ is chosen or the class of odd permutations.
Therefore, we will always have to deal with this ambiguity in all our constructions as each ordering that we use is, in fact, an equivalence class of orderings. For example,
- $ABC$ means $[ABC]=\{ABC,BCA,CAB\}$; and
- $ACB$ means $[ACB]=\{ACB,CBA,BAC\}$. $\\$
The good news is, it suffices to list a single representative of the class to orient the simplex.
Exercise. Demonstrate how this scheme fails for cubical complexes. Hint: try dimension $2$.
Exercise. With the meaning of orientation of cells of dimensions $1$ and $2$ clear, what could be the meaning of orientation of a vertex?
The algebra of oriented chains
In this section, our ring of coefficients is either ${\bf R}$ or ${\bf Z}$.
Definition. Suppose a simplicial complex $K$ consists of simplices as subsets of set $S$. We say that $K$ is an oriented simplicial complex if its every simplex is oriented. (We will omit “oriented” when there can be no confusion.)
Example. The simplicial complex $K$ of the triangle is $$\begin{array}{llllllllll} \text{unoriented: } &K=\big\{\{A\},&\{B\},&\{C\},&\{A,B\},&\{C,B\},&\{A,C\},&\{A,B,C\}\big\}; \text{ or}\\ \text{oriented: } &K=\{A,&B,&C,&AB,&CB,&AC,&[ABC]\}. \end{array}$$
Note that the orientations of the edges of $\tau$ don't match the orientation of $\tau$ itself. The reason is, they don't have to... We shouldn't expect such a requirement because there may be another $2$-simplex adjacent to one of these edges with the opposite orientation. $\square$
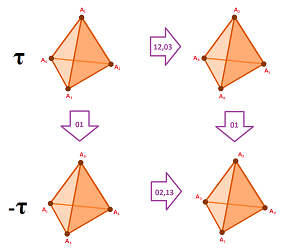
To acquire an orientation for complex $K$, one can just order its vertices and then use that order to orient each simplex in $K$:
Exercise. In how many ways can this be done?
Up to this point, the development of the algebra of chains follows the same path as in the case of oriented cubical complexes. Let's point out some differences. First, all simplices have to be supplied with orientations not just $1$-dimensional ones. Second, the meaning of $-\tau$ for a simplex $\tau$ is clear: it's $\tau$ with the opposite orientation. For dimensions $1$ and $2$, the explicit meaning is also clear:
For higher dimensions, it's a transposition of two vertices in the ordering: $$A_1A_0A_2 ... A_n=-A_0A_1A_2 ... A_n.$$
It is worth repeating what oriented simplices are and aren't.
- Oriented simplices aren't sets of the vertices: not $\{A,B,C\}$.
- Oriented simplices aren't orderings of the vertices: not $ABC$.
- Oriented simplices are classes of orderings of the vertices, such as $[ABC]=\{ABC,BCA,CAB\}.$
This is how we make it precise.
Theorem. For any permutation $s\in \mathcal{S}_{n+1}$, we have: $$A_0A_1 ...A_n = \pi (s) A_{s(0)}A_{s(1)} ...A_{s(n)},$$ where $\pi (s)$ is its parity, i.e., $$\pi(s):=\begin{cases} 1&\text{if } s \text{ is even},\\ -1&\text{if } s \text{ is odd}. \end{cases}$$
Recall that the point of using oriented chains is to be able to capture all possible ways to go around the circle: going once, twice, or thrice around it, or going in the opposite direction.
An oriented simplicial chain is a “formal” linear combination of finitely many oriented simplices, such as $3a + 5b - 17c$. The coefficients come from some ring $R$. From this point of view, the chains previously discussed are over $R={\bf Z}_2$, i.e., binary. We will concentrate on real chains, i.e., ones with real coefficients. Nonetheless, the analysis will, with just a few exceptions, apply also to the integers $R={\bf Z}$, rational numbers $R={\bf Q}$, etc.
Next, for a given simplicial complex $K$ and $k=0,1,2,...$, let $C_k(K)$ denote the set of all real $k$-chains: $$C_k(K) := \left\{\displaystyle\sum_is_i \sigma_i :\ s_i \in {\bf R}, \sigma_i \text{ is a } k\text{-simplex in } K \right\}.$$
It is easy to define the sum of two chains by assigning appropriate coefficients of each simplex: if $$A = \displaystyle\sum_i s_i \sigma_i, B = \displaystyle\sum_i t_i \sigma_i \Longrightarrow A + B := \displaystyle\sum_i(s_i + t_i) \sigma_i.$$ To see that the operation above is well-defined, one can assume that each sum lists all simplices present in both sums -- some with zero coefficients.
Theorem. $C_k(K)$ is an abelian group with respect to chain addition.
Proof. We verify the axioms of group below.
- (1) Identity element:
$$0 = \displaystyle\sum_i 0 \cdot \sigma_i.$$
- (2) Inverse element:
$$A = \displaystyle\sum_i s_i \sigma_i \Longrightarrow -A = \displaystyle\sum_i (-s_i)\sigma_i.$$
- (3) Associativity:
$$\begin{array}{lllll} &A + (B + C) &= \displaystyle\sum_i (s_i + t_i + u_i) \sigma_i \\ \hspace{.26in}&&= (A + B) + C.&\hspace{.26in}\blacksquare \end{array}$$
It is also easy to define the scalar multiplication of chains: if $$A = \displaystyle\sum_i s_i \sigma_i, \text{ and } r\in {\bf R},$$ then we let $$rA := \displaystyle\sum_i(rs_i) \sigma_i.$$
Theorem. (1) $C_k(K;{\bf R})$ is a vector space with respect to chain addition and scalar multiplication with a basis that consists of all $k$-simplices in $K$. (2) $C_k(K;{\bf Z})$ is an abelian group with respect to chain addition with the set of generator that consists of all $k$-simplices in $K$.
Exercise. Prove the theorem.
Example. In particular, in the example of a triangle representing the circle, we have
- $C_0(K) = <A> \cong {\bf R},$
- $C_1(K) = <a,b,c> \cong {\bf R} \oplus {\bf R} \oplus {\bf R},$
- $C_2(K) = 0$, etc. $\square$
Exercise. Prove that choosing a different orientation of a simplicial complex produces a chain group isomorphic to the original. Present the matrix of the isomorphism.
Exercise. What does the algebra of oriented chains over ${\bf Z}_2$ look like?
Until some connection is established between chains of different dimensions, this algebra has nothing to say about the topology of the complex. This connection is given by the boundary operator.
The boundary operator
The boundary operator of a simplicial complex records the relations between cells/chains of consecutive dimensions.
Let's review what we already know.
Example. Suppose we have a simplicial complex $K$ of the solid triangle seen before:
- $0$-simplices: $A, B, C$;
- $1$-simplices: $a = AB,\ b = CB,\ c = AC$;
- $2$-simplex: $\tau = ABC$.
The boundary of a vertex empty, hence the boundary operator of a $0$-chain is $0$: $$\partial (A) = 0, \ \forall A \in C_0(K).$$ The boundary of a $1$-cell consists of its two endpoints, so, in the binary setting, this was simple: $$\partial (a) = \partial (AB) = A + B.$$ In the oriented setting, the direction of the edge matters ($AB \ne BA$); so we define: $$\partial (a) = \partial (AB) := B - A, \ \forall a = AB \in C_1(K).$$ In dimension $2$, the boundary $\partial \tau$ is defined as a linear combination of its faces: $$\partial \tau = AB + BC + CA = a - b - c,$$ or: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{lllllll} \partial \tau & = & \partial \Big( \bigtriangleup \Big) \\ & = & \nearrow + & \searrow + & \leftarrow \\ & = & a+ & (-b)+ & (-c) \\ & = & a-b-c. \end{array} $$ Here, we first follow the chain clockwise as indicated by its orientation writing the $1$-cells as they appear, and then interpret these $1$-cells in terms of the $1$-cells, $a, b, c$, that we listed in the complex $K$. $\square$
Let's define the boundary of a simplex of an arbitrary dimension.
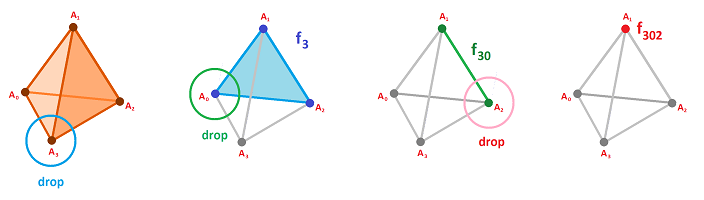
Recall first what we mean by a face of a simplex. As the $n$-simplex is just a list of $n+1$ vertices, any of its $(n-1)$-faces is a list of the same vertices with one dropped: $$\begin{array}{lll} f_0 &= [A_0]A_1 ... A_n ,\\ f_1 &= A_0[A_1] ... A_n ,\\ &...\\ f_n &= A_0A_1 ... [A_n]. \end{array}$$
The question now is, what are the oriented faces of an oriented simplex? The answer is, of course, they are oriented simplices.
The idea is very simple: removing an item from an ordering gives an ordering of the smaller set, just as shown above. Yet, to see that this answer is justified isn't as simple as it seems. Indeed, we aren't dealing with orderings but with classes of orderings. Does this operation make sense?
Proposition. Removing an item from an even/odd ordering gives us an even/odd ordering of the smaller set; or, algebraically, $$\mathcal{A}_n=\mathcal{S}_n\cap \mathcal{A}_{n+1} .$$
Exercise. Prove the proposition.
Now, the boundary of an $n$-simplex $s$ is the sum of its faces, in the unoriented case. As we see in the last example, this time the faces appear with various signs. As it turns out, the boundary now is the alternating sum of its faces: $$\partial s = f_0 - f_1 + f_2 - ... \pm f_n.$$
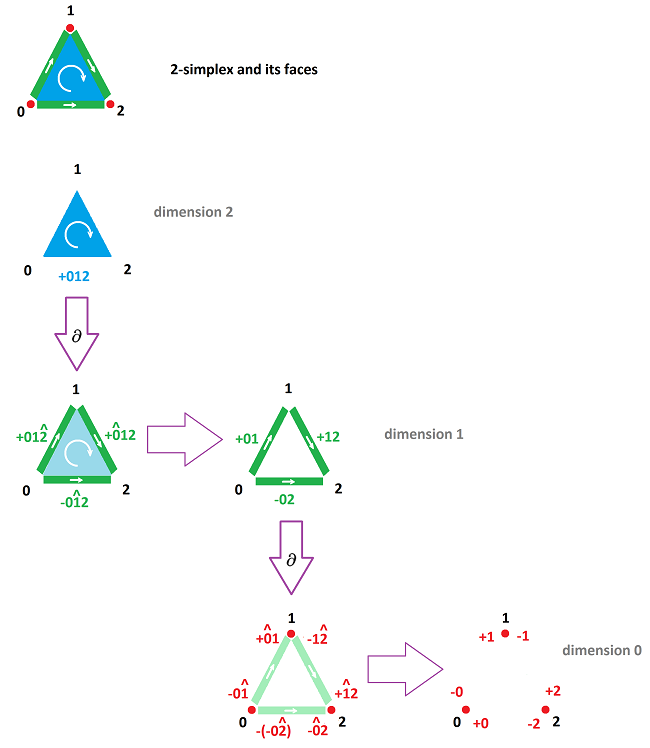
Definition. The boundary of an oriented $n$-simplex is an oriented $(n-1)$-chain defined to be $$\partial (A_0A_1 ... A_i ... A_n) := \sum_i (-1)^i A_0A_1 ... [A_i] ... A_n .$$
Example. Let's apply the definition to the complex of the triangle, as in the last example. These are the oriented simplices based on the obvious ordering of the $3$ vertices:
- $0$-simplices: $A_0, A_1, A_2$;
- $1$-simplices: $A_0A_1, A_1A_2, A_0A_2$;
- $2$-simplex: $A_0A_1A_2$. $\\$
Then $$\begin{array}{llll} \partial (A_0A_1A_2) &= [A_0]A_1A_2 - A_0[A_1]A_2 + A_0A_1[A_2] \\ &= A_1A_2 - A_0A_2 + A_0A_1 \\ &=A_0A_1 + A_1A_2 +A_2A_0 . \end{array}$$ So, these edges go clockwise around the triangle, as expected. $\square$
Notice that the input of the formula in the definition is an ordering while it is supposed to be an oriented simplex, i.e., a class of orderings. What happens if we use another representative from the class of orderings as the input of this formula?
Exercise. Confirm that the result is the same for $\partial (A_2A_0A_1)$.
A single term in the boundary formula for a $2$-simplex is shown below:
To further understand what's going on, let's flip the first two vertices: $$\begin{array}{llll} \partial (A_1A_0A_2 ... A_n) \\ = \sum_i (-1)^i A_1A_0A_2 ... [A_i] ... A_n \\ = [A_1]A_0A_2 ... A_n - A_1[A_0]A_2 ... A_n &+ \sum_{i>1} (-1)^i A_1A_0A_2 ... [A_i] ... A_n \\ = A_0A_2 ... A_n - A_1A_2 ... A_n &+ \sum_{i>1} (-1)^i A_1A_0A_2 ... [A_i] ... A_n \\ = -A_1A_2 ... A_n + A_0A_2 ... A_n &+ \sum_{i>1} (-1)^i (-1)A_0A_1A_2 ... [A_i] ... A_n \\ = -[A_0]A_1A_2 ... A_n + A_0[A_1]A_2 ... A_n &- \sum_{i>1} (-1)^i A_0A_1A_2 ... [A_i] ... A_n \\ = -\sum_i (-1)^i A_1A_0A_2 ... [A_i] ... A_n \\ = -\partial (A_0A_1A_2 ... A_n). \end{array}$$ The sign of the boundary chain has reversed! Therefore, we have the following:
Theorem. The boundary chain of an ordered simplex is well-defined. In particular, for any oriented simplex $s$, we have $$\partial (-s)= -\partial (s).$$
Exercise. Provide the rest of the proof.
With the operator defined on each of the simplices, one can extend this definition to the whole chain group by linearity, thus creating a linear operator: $$\partial : C_n(K) \to C_{n-1}(K).$$ Indeed, since we know $\partial (\sigma_i)$ for each simplex $\sigma_i \in C_n(K)$, we set: $$\partial \Big( \displaystyle\sum_i s_i \sigma_i \Big) := \displaystyle\sum_i s_i \partial( \sigma_i ).$$
The Double Boundary Identity
Theorem (Double Boundary Identity). $\partial \partial = 0$, with coefficient over ${\bf R}$ or ${\bf Z}$.
Proof. It suffices to prove that $\partial \partial (s) = 0$ for any simplex $s$ in $K$. The idea is that in the expansion of $\partial \partial s$, each $(n-2)$-face appears twice but with opposite signs.
Suppose $s$ is an $n$-simplex: $$s=A_0 ... A_n .$$ For each $i=0,1, ...,n$, $f_i$ is the $i$th face of $s$: $$f_i=A_0 ... [A_i] ... A_n.$$ It is an oriented $(n-1)$-simplex. For each pair $i,j=0,1, ...,n,\ i \ne j$, let $f_{ij}=f_{ji}$ be the $j$th face of $f_i$ or, which is the same thing, the $i$th face of $f_j$: $$f_{ij}=A_0 ... [A_i] ... [A_j] ... A_n.$$ It is an oriented $(n-2)$-simplex.
First, we use the definition and then the linearity of the boundary operator: $$\begin{array}{llllll} \partial \partial s &= \partial \Big( \sum_i (-1)^i f_i \Big) \\ &= \sum_i (-1)^i \partial( f_i ) . \end{array}$$ Consider the $i$th term, i.e., the summation over $j$, and watch how the signs alternate: $$\begin{array}{lllllll} \partial f_i &=\partial(A_0 A_1 ... [A_i] ... A_n ) \\ &= \displaystyle\sum_{j < i} (-1)^j A_0A_1 ... [A_j] ... [A_i] ... A_n &\text{ $[A_j]$ in the $j$th term of the sum...} \\ &+ \displaystyle \sum_{j > i} (-1)^{j-1} A_0 A_1 ... [A_i] ... [A_j] ... A_n &\text{ $[A_j]$ in the $(j-1)$st term...} \\ &= \displaystyle \sum_{j < i} (-1)^j f_{ij} + \displaystyle \sum_{j < i} (-1)^{j-1} f_{ij} . \end{array}$$ So, the sign attached to the face becomes the opposite as $j$ goes past $i$. That's what will ensure cancelling...
We substitute now and then deal with double summation, over $i$ and $j$: $$\begin{array}{lllllll} \partial \partial s & = \displaystyle \sum_i (-1)^i \Big(\displaystyle \sum_{j < i} (-1)^j f_{ij} + \displaystyle \sum_{j < i} (-1)^{j-1} f_{ij} \Big) \\ &= \displaystyle \sum_{i < j} (-1)^{i+j} f_{ij} - \displaystyle \sum_{i > j} (-1)^{i+j} f_{ij} \\ &=0. \end{array}$$
Let's summarize what has happened. The $(n-2)$-faces of our simplex $s$ form a symmetric $(n+1)\times (n+1)$ matrix. Then $\partial \partial s$ is the sum of the elements of this matrix, with appropriate signs, after the diagonal is removed: $$\{f_{ij}\}=\left[ \begin{array}{c|ccc|c|c|c|cc} &0 &1 &...&i &...&j &...&n\\ \hline 0&0 &-f_{01}&...&+f_{0i}&...&-f_{0j}&...&+f_{0n}\\ 1&+f_{10}&0 &...&-f_{1i}&...&+f_{1j}&...&-f_{1n}\\ &.&.&...&.&...&.&...&.\\ &.&.&...&.&...&.&...&.\\ \hline i&-f_{i0}&+f_{i1}&...&0 &...&-f_{ij}&...&+f_{in}\\ \hline &.&.&...&.&...&.&...&.\\ &.&.&...&.&...&.&...&.\\ \hline j&+f_{j0}&-f_{j1}&...&+f_{ji}&...&0 &...&-f_{jn}\\ \hline &.&.&...&.&...&.&...&.\\ &.&.&...&.&...&.&...&.\\ n&-f_{n0}&+f_{n1}&...&-f_{ni}&...&+f_{nj}&...&0 \end{array} \right]$$ Finally, the symmetric entries have opposite signs and, therefore, cancel. $\blacksquare$
Exercise. Fill the blanks in the table to demonstrate how the signs alternate.
The diagram below illustrates the proof for $n=2$:
Corollary. The theorem holds for chains over ${\bf Z}_2$.
Exercise. Prove the corollary (a) by rewriting the above proof, (b) directly from the theorem. Hint: think of an appropriate function ${\bf Z}\to {\bf Z}_2$.
So, the boundary of the boundary of a cell is zero. Since every chain is a linear combination of cells, it follows from the linearity of $\partial$ that the boundary of the boundary of any chain is zero; i.e., $$\begin{array}{llllll} C_k(K) & \xrightarrow{\partial} & C_{k-1}(K) & \xrightarrow{\partial} & C_{k-2}(K) \\ \tau & \mapsto & \partial (\tau ) & \mapsto & \partial \partial (\tau )=0. \end{array}$$
Thus, every boundary is a cycle: $$B_k(K) \subset Z_k(K).$$