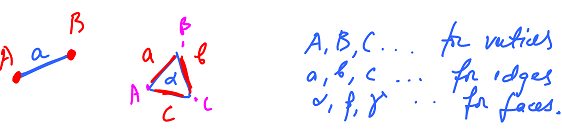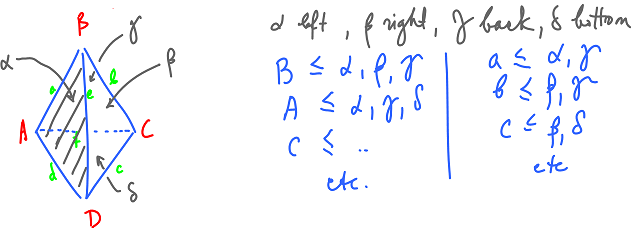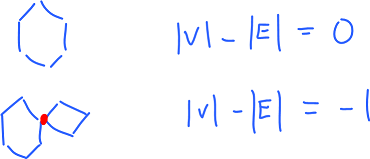Polyhedron

Polyhedra are unions of polygons (faces) attached to each other along the edges.

Next we want the polyhedron to look like a surface, for the Euler's theorem.

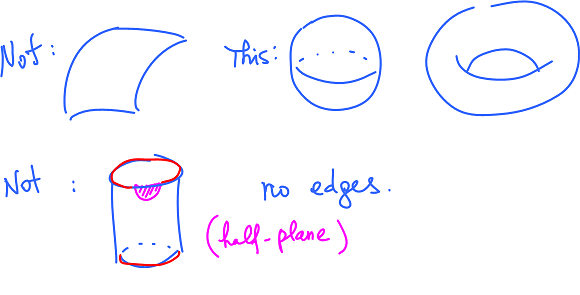
In common: locally look like a plane!

Should be familiar! Curves locally look like a straight line.

How do we ensure That our polyhedron is a surface?

Find conditions on the polygons that make up the polyhedron that ensure that this is a surface.

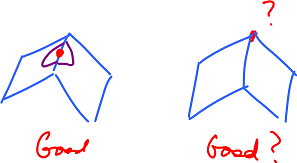
Start: every vertex $V$ should be surrounded by faces.

What is a polyhedron for the Euler's theorem? We need a combinatorial description!

A polyhedron is made of these pieces:

• vertices -- set $V$ -- endpoints of...
• edges -- set $E$ -- boundaries of...
• faces -- set $F$.

Example.

We set up a partial order: $$A < a,c;B < a,b;C<c,b;$$ $$a,b,c < \alpha.$$ It is about the boundary relation: $x<y$ if $x$ is a part of the boundary of $y$.

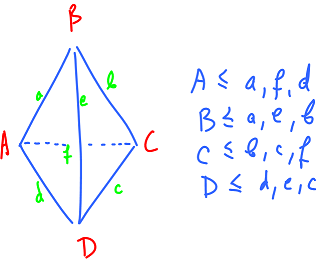
Example. A wire-frame:

Take this, we can reconstruct the polyhedron.

What about the sphere/surface?

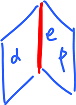
Rule 1: Every edge is contained in exactly two faces.

Combinatorially: for each $e \in E$ there exist exactly two (distinct) $\alpha,\beta \in F$ such that $e,\alpha,e<\beta$.

With this condition, does this have to be surface?

ex: just a point, no edges

So, one edge -- two faces etc.

Requirement:

• edges intersect by vertices,
• faces intersect by edges.

Definition of surface = every point has a neighborhood homeomorphic to the the disk.

Rule 1 ensured that this is true for every point inside an edge:

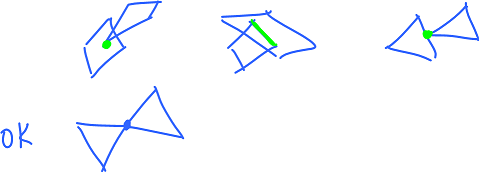
Exercise. Find an example: Rule 1 but not a surface.

Now vertices...

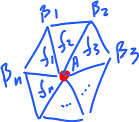
Rule 2: Every vertex is "surrounded" by faces.

Given $A \in V$, there are $f_1,..., f_n$ such that $$A<f_1,..., f_n$$ and there are $B_1,..., B_n \in V$, such that $$B_n = B_0$$ and $$AB_k < f_k,f_{k+1} ({\rm mod} n).$$

Next, the sphere as a specific surface...

1. 1: It's connected!

To be precise it "path-connected": Any 2 points can be connected by a path.

Two vertices.... a path made of edges.

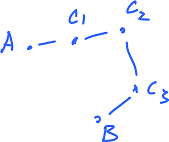
Translate: Given two vertices $A, B \in V$, $A \ne B$, there are $C_1,...,C_n \in V$ such that

• $AC_1 \in E,$
• $C_1C_2 \in E,$
• ...
• $C_nB \in E.$

This is "edge path-connectedness".

Path-connectedness: in a topological space $X$, for any two points $A, B \in X$, three is a cont. function

• $f:[0,1] \to X$ such that $f(0)=A,f(1)=B$.

Note the difference:

• Looser: only vertices have to be connected.
• Tighter: you have to use edges for the path.

Proposition. Path-connectedness <=> edge path connectedness (for polyhedra).

Exercise. idea: face at a time.

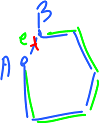
Second, how do we exclude the torus?

Does any loop divides it into two pieces?

A loop is a closed path, should be made of edges.

A path is

• a sequence of edges $a_1,...,a_n \in E$,
• a sequence of vertices $A_1,...,A_{n+1} \in V$,

such that $a_k= A_k A_{K+1}$.

If, in addition, $A_1 = A_{n+1}$, then the path is called a loop.

"Two pieces" = disjoint = not path connected = there is no path between some points.

Euler's Theorem. P is a polyhedron w/ $V, E, F$. Assume

1. $P$ is path connected;
2. Every loop cuts $P$ into two disjoint pieces.

Then $$|V|-|E|+|F|=2.$$

Let explore first.

How? Consider analogue for dimension $1$.

It's "polygon" instead! Or it can be described as a graph:

Theorem. $G$ is a graph,

• $G$ is path connected;
• $G - A$ is path connected, A is a vertex;
• every vertex is an end-point of exactly two edges (two edges share 2 or 0 vertices).

Then $$|V|-|E|=0.$$

Proof.

There is a path in $P - e$ between $A$ and $B$, and

• number of edges = number of vertices - 1.

Remains: show there are no other vertices or edges (exercise). $\blacksquare$

Exercise. Look at the details.

Exercise. What about trees?

More on graphs, topologically...

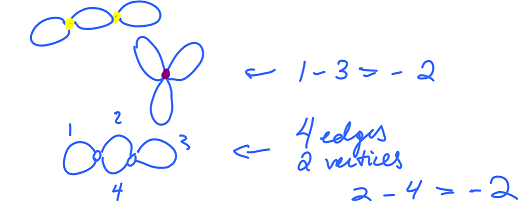
What it there are self-intersections?

Circle and figure eight:

Let's describe first... Conditions 1 and 2 are satisfied and 3 too except for one special vertex. This vertex separates the graph into 2 parts.

They are different! But what's in common?

• Loops: 1 loop, 2 loops, 3 loops
• Euler characteristic: 0, -1, -2.

So, the answer is topology. For more see Euler-Poincare formula

Euler's theorem again.

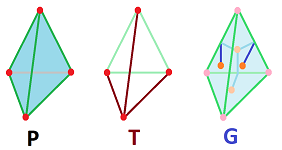
Idea of proof: build two graphs on the polyhedron $P$.

• $T$ captures all vertices of P and some edges.
• $\Gamma$ captures all faces of $P$ and the rest of the edges.

Now, this what we know:

• $V_T-E_T=1$
• $V_{\Gamma}-E_{\Gamma}=1$

Add them:

• $V_T-(E_T+E_{\Gamma})+V_{\Gamma}=2$

These three terms are

• vertices + edges = faces

of $P$. And the theorem follows.

We need $T$ and $\Gamma$ satisfying 1 and 2.

Lemma. Every graph has a subgraph which

• contains all of the original vertices and
• is a tree.

Start w/ the $1$-skeleton of $P$, which is a graph $G$ (edges). Then, by lemma, find a subgraph $T$ which is a tree, w/ vertices = vertices of $P$.

Idea of $\Gamma$, the dual graph of $T$. Then

1. $T$ is connected -- check
2. $T$ is a tree.

It is defined as follows:

• $\Gamma$'s vertices are "middle points" of the faces.
• $\Gamma$'s edges connect $\Gamma$'s vertices by crossing the edges of $P$, but not one's of $T$.

1) It is always possible to get from one face to any adjacent face w/o crossing $T$. Why?

Otherwise the two faces would be separated by a loop of $T$, not possible, as there are no loops in $T$.

2) T is a tree. Why?

If there is a loop in, the loop would separate $P$ into 2 pieces, which contradicts condition 2.