This site is being phased out.
Parametric complexes
Contents
- 1 Topology and uncertainty
- 2 Persistence of homology classes
- 3 The homology of a gray scale image
- 4 Homology groups of filtrations
- 5 Maps of filtrations
- 6 The “sharp” homology of a gray scale image
- 7 Persistent homology groups of filtrations
- 8 Other instances of parametric spaces
- 9 Multiple parameters
Topology and uncertainty
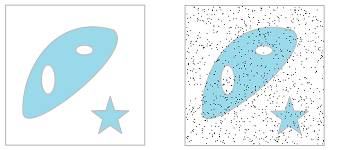
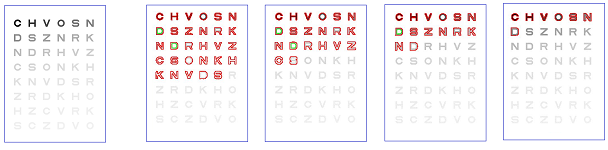
So far, homology has been used to describe the topology of abstract geometric objects. The nature of these objects, then, dictated that all homology classes receive equal attention. Meanwhile, converting such real-life data as digital images into cell complexes requires extra steps that may lead to uncertainty and a loss of information:
Above, we see how subtle variations of gray may be discarded. In addition, the topology of digital images and other data may be “corrupted” by noise:
This kind of “salt-and-pepper” noise is normally dealt with by removing the components that are smaller than, say, a couple of pixels. The implicit assumption for this to work is that a pixels are really small! However, misplacing just one could dramatically change the topology of the image:
The example shows that adding the red pixel merges two components, while adding the green one creates a hole.
We will learn how to rank homology classes according to their relative importance, called persistence, and attempt to discard the noise.
Since it's not known beforehand what is or is not noise in the dataset, we need to capture all homology classes including those that may be deemed noise later. We will introduce an algebraic structure that contains, without duplication, all these classes. Each of them is associated with its persistence and can be removed when the threshold for acceptable noise is set.
Let's consider the two basic real-life sources of datasets.
Example (gray scale images). A gray scale image is a real-valued function $f:R\to {\bf R}_+$ defined on a rectangle $R$. Then, given a threshold $r$, its lower level set $f^{-1}((-\infty,r))$ can be thought of as a binary image on $R$. Each black pixel of this image is treated as a square cell in the plane. This process is called thresholding, which is also applicable to the $n$-dimensional case. Of course, these $2$-dimensional cells are combined with their edges ($1$-cells) and vertices ($0$-cells). The result is a cubical complex $K$ for each $r$.
$\square$
Example (point clouds). A point cloud is a finite set $S$ in some Euclidean space of dimension $d$. Given a threshold $r$, we deem any two points that lie within $r$ from each other to be “close”. In that case, this pair of points is connected by an edge. Further, if three points are “close” to each other -- in the sense that the diameter of this triangle is less than $r$ -- we add a face spanned by these points. If there are four, we add a tetrahedron, and, finally, any $d+1$ “close” points create a $d$-cell. The process is called the Vietoris-Rips construction. The result is a simplicial complex $K$ for each $r$.
$\square$
Next, we would like to quantify the topology of what's behind this data -- with homology groups. Instead of using a single threshold and studying a single cell complex, one considers all thresholds and all possible cell complexes. Since increasing threshold $r$ enlarges the corresponding complex, we have a sequence of complexes: $$K^{1} \hookrightarrow K^{2} \hookrightarrow K^{3} \hookrightarrow ... \ \hookrightarrow K^{s},$$ where the arrows represent the inclusions: $$i^{n}: K^{n} \hookrightarrow K^{n+1}.$$ This sequence denoted by $$\{K^{n}\}=\{K^{n},i^{n}:\ n=1,2,3,...,s-1\}$$ is called a filtration.
The elements of filtration can also be topological spaces. Provided these spaces are polyhedra, the homology groups are well defined and each of the inclusions generates its homology map: $$i_*^{n}:H(K^{n}) \to H(K^{n+1}).$$ As a result, we have a sequence of homology groups connected by these homomorphisms: $$H(K^{1}) \to H(K^{2}) \to \ ...\ \to H(K^{s})\to 0, $$ with $0$ added for convenience. These homomorphisms record how the homology changes as this “parametric” space grows at each step. For example, a component appears, grows, and then merges with another one; or a hole is formed, shrinks, and then is filled. We refer to these events as birth and death of the corresponding homology class.
In order to evaluate the relative importance of an element of one of these groups, the persistence of a homology class is defined as the number of steps in the homology sequence it takes for the class to end at $0$. In other words, $$persistence = death - birth.$$ Indirectly, this number reflects the robustness of the homology class with respect to the changing parameter.
Exercise. Describe the homology of the filtrations in the above examples.
Persistence of homology classes
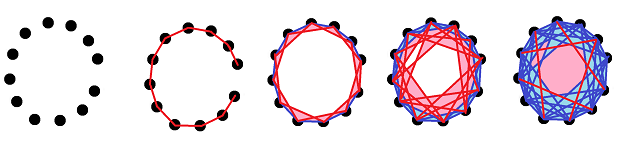
While constructing a simplicial complex from a point cloud, we gradually add cells of various dimensions in hope of being able to discover the topology of the object. For example, what comes out of a point cloud of a circle might look like this:
But how do we know which one of these complexes is the “true” representation of the circle without actually looking at it? In other words, how would a computer see a circle behind this data?
A simpler question is, how can we tell which cycle in which of these complexes captures the hole of the circle, without us looking at it to confirm?
To try to answer this question, we look at the whole sequence and how it develops. The idea is to measure and compare the life-spans of these cycles.
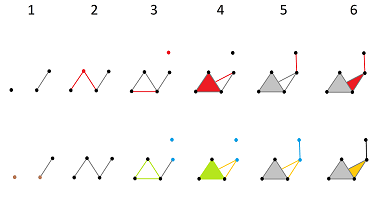
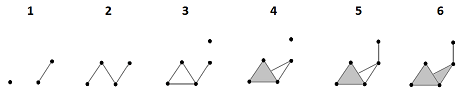
Example (homology of filtration). Let's take a simpler example and provide complete computations:
The top row is the sequence of the complexes of the filtration, which looks like a sequence of frames in a movie. In each of these “frames”, the new cells are marked in red. In the bottom row, the new cycles are given in various colors:
- The brown $0$-cycle appears in the 1st frame and dies in the 2nd.
- The blue $0$-cycle appears in the 3rd frame and dies in the 5th.
- The green $1$-cycle appears in the 3rd frame and dies in the 4th.
- The orange $1$-cycle appears in the 4th frame and dies in the 6th.
The importance of a homology class is then evaluated by the length of its life-span: how long it takes for the class to disappear as it is mapped to the next frame. In other words, the persistence is equal to how many applications of these homology maps it takes for the homology class to become $0$.
The values are given below.
- The brown $0$-class appears in the 1st frame and dies in the 2nd: persistence $1$.
- The blue $0$-class appears in the 3rd frame and dies in the 5th: persistence $2$.
- The green $1$-class appears in the 3rd frame and dies in the 4th: persistence $1$.
- The orange $1$-class appears in the 4th frame and dies in the 6th: persistence $2$.
Now, in order to settle on a particular topology, we choose a threshold for persistence. If the choice is $1$, then we keep all these cycles: two $0$-cycles and two $1$-cycles. If, however, the choice is $2$, there is only one of each. Which of the two is the “correct” one remains a judgement call.
Instead of looking at one class at a time, we list the homology groups (over ${\bf R}$) and the homology maps of the whole filtration: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\ #1 \ }\!\!\!\!\!} % \begin{array}{ccccccccccccccccccccc} & H_n(K^{1}) & \ra{i_*^1} & H_n(K^{2}) & \ra{i_*^2} & H_n(K^{3}) & \ra{i_*^3} & H_n(K^{4}) & \ra{i_*^4} & H_n(K^{5}) & \ra{} & 0\\ n =0: & {\bf R}\oplus {\bf R} & \ra{[1,1]} & {\bf R} & \ra{[1,0]^T} & {\bf R}\oplus {\bf R} & \ra{\operatorname{Id}} & {\bf R}\oplus {\bf R} & \ra{[1,1]} & {\bf R} & \ra{0} & 0 \\ n =1: & 0 & \ra{0} & 0 & \ra{0} & {\bf R} & \ra{[0,1]^T} & {\bf R} & \ra{\operatorname{Id}} & {\bf R} & \ra{0} & 0 \end{array}$$
$\square$
Exercise. Compute the compositions of the homology maps of the inclusions and compare them to the values of the persistence.
Exercise. Find the homology maps of the inclusions of this filtration:
$$\begin{array}{ccccccccccccccccccccc} \dim = 0: & {\bf R}\oplus {\bf R} & \to & {\bf R} & \to & {\bf R}\oplus {\bf R} & \to & {\bf R}\oplus {\bf R} & \to & {\bf R} & \to & 0 \\ \dim = 1: & 0 & \to & 0 & \to & {\bf R} & \to & {\bf R} & \to & 0 & \to & 0 \end{array}$$
Example (blurring). Let's analyze this image of a blurred disk:
We use all $255$ levels of gray as thresholds. Then each of the complexes is a disk and the homology groups of the filtration are very simple:
$$\begin{array}{ccccccccccccccccccccccc} \dim = 0: & {\bf R} & \to & {\bf R} & \to & {\bf R} & \to & ... & \to & {\bf R} & \to & 0. \end{array}$$ Also, the inclusions generate the identity maps on homology: $i^n_*=\operatorname{Id}$. So, if we assume that the center of the circle is pure black (value $0$) and the outside is pure white (value $255$), then the persistence of the smallest circle is $255$.
$\square$
Exercise. A car or a motorcycle? Use thresholding to create a filtration, find its homology groups and the persistence of all homology classes for each of these images of headlights:
Consider, in contrast, the persistence analysis of binary images.
Suppose a binary picture of a real-life object is taken with a higher and higher resolution. The result is a sequence of cubical complexes. At step $n$, one assigns a given pixel to the complex whenever the image of the object crosses it. As a result we have a decreasing sequence of complexes: $$K^s\supset K^{s-1}\supset ... \supset K^1 . $$
It is natural to think that each topological feature in the space being discretized is captured by at least one of the elements of the filtration. The example below shows that the converse isn't always the case.
Example (artifacts). Here we discretize a triangle (left) with grids of better and better resolution.
In each case, the result has the same problem: there is an extra, one-pixel hole that's not present in the original!
Or is it? The last image on the right shows the left bottom corner of the original zoomed in, and a disconnected pixel (hole) is visible. One can reproduce this effect with MS Paint or other similar software. Therefore, improving the resolution won't eliminate the spurious hole.
Now, these four images -- going from right to left -- form a filtration: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{cccccccccccccccccccc} & H_1(K^{1}) & \ra{i_*^1} & H_1(K^{2}) & \ra{i_*^2} & H_1(K^{3}) & \ra{i_*^3} & H_1(K^{4}) & \ra{} & 0\\ n = 1: & {\bf R} \oplus {\bf R} & \ra{\operatorname{Id}\oplus 0} & {\bf R} \oplus {\bf R} & \ra{\operatorname{Id} \oplus 0} & {\bf R} \oplus {\bf R} & \ra{\operatorname{Id} \oplus 0} & {\bf R} & \ra{0} & 0 \end{array} $$ Since the homology groups are identical, the extra hole might appear -- incorrectly -- persistent. The good news is that the issue is resolved by the homology maps. At every step, the homology class of the spurious hole goes to zero under the homology map of the inclusion. Therefore, the persistence of each of these holes is equal to the lowest possible value of $1$!
$\square$
Exercise. What geometric figure on the plane will always have, under this kind of discretization, an extra component -- no matter how much the resolution is improved?
Now, the idea of the persistence of homology classes of the $i$th complex $K^i$ -- as a part of the filtration -- becomes clear. The non-persistent ones go to $0$. Then, together, they form the kernel of the homology map of the inclusion. The persistent ones are “what's left”. Initially, one can think of this part as the orthogonal complement of the kernel. So,
- the $0$-persistent homology group $H^0_n(K^i)$ of complex $K^i$ is simply its homology group;
- the $1$-persistent homology group $H^1_n(K^i)$ is the orthogonal complement of the kernel of the homology map of the inclusion of the complex into the next one;
- the $2$-persistent homology group $H^2_n(K^i)$ is the orthogonal complement of the kernel of the homology map of the composition of the two inclusions;
- etc.
Of course, the orthogonal complement can be understood as a quotient.
Definition. The $p$-persistent homology group of the $i$th element $K^i$ of filtration $\{K^n\}$ is defined to be $$H^p(K^i):=H(K^i) / \ker i_*^{i,i+p},$$ where $i^{i,i+p}:K^i\to K^{i+p}$ is the inclusion.
Exercise. Compute the persistent homology groups of each of the filtrations depicted in the subsection.
Can we combine these groups $H^p_n(K^1), H^p_n(K^2),...,H^p_n(K^s)$ into one?
The homology of a gray scale image
Putting the persistence issue aside for now, we will try to understand the meaning of the homology of a gray scale image, taken “as is”.
For a complete analysis, let's take this simple image on the left:
We assume that only these four colors -- white, light gray, dark gray, and black -- are in play.
First the image is thresholded. The lower level sets of the gray scale function of the image form a filtration: a sequence of three binary images, i.e., cubical complexes: $$K^{1} \hookrightarrow K^{2} \hookrightarrow K^{3},$$ where the arrows represent the inclusions $i^{1},i^{2}$. Here, white means empty. For completeness sake, one can add a fully white image in the beginning and fully black in the end of the sequence.
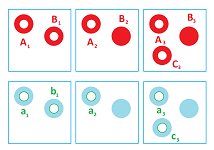
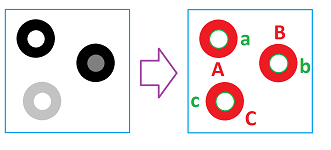
We go clockwise starting at the upper left corner and use the following for $i=1,2,3$:
- $A_{i},B_{i},C_{i}$ are the $0$-homology classes that represent the components of $K^{i}$; and
- $a_{i},b_{i},c_{i}$ are the $1$-homology classes that represent the holes.
The homology groups of these images also form sequences -- one for either dimension $0$ and $1$.
Then $i_*^{1},i_*^{2}$ are the two homology maps of the inclusions while $i_*^{3}=0$ is included for convenience. These homomorphisms map the generators, as follows: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{#1}\!\!\!\!\!} \begin{array}{cccccccccccccccccccccc} & i_*^{1} & & i_*^{2}& & i_*^{3} \\ A_{1} & \mapsto & A_{2} & \mapsto & A_{3} & \mapsto & 0 \\ B_{1} & \mapsto & B_{2} & \mapsto & B_{3} & \mapsto & 0 \\ & & & & C_{3} & \mapsto & 0 \\ a_{1} & \mapsto & a_{2} & \mapsto & a_{3} & \mapsto & 0 \\ b_{1} & \mapsto & 0 & & & & \\ & & & & c_{3} & \mapsto & 0 \end{array} $$
In order to avoid double counting, we want to count only the homology generators that don't reappear in the next homology group. To do so, a more algebraically convenient way is to capture the homology classes taken to $0$ by these homomorphisms. These classes form the kernels of $i_*^{1},\ i_*^{2},\ i_*^{3}$.
Finally, as a simple way to combine these classes, the homology group of the original, gray-scale image is chosen to be the direct sum of these kernels: $$H_{0}(\{K^{i}\}) = <A_{3},B_{3},C_{3}>,$$ $$H_{1}(\{K^{i}\}) = <b_{1},a_{3},c_{3}>.$$ The data shows that image has three components and three holes, as expected.
To summarize, the $0$- and $1$-homology groups of the frames of the gray scale image, $${\bf R}^2 \to {\bf R}^2 \to {\bf R}^3 \to 0,$$ $${\bf R}^2 \to {\bf R}^1 \to {\bf R}^2 \to 0,$$ produce its homology groups: $$H_{0}(\{K^{i}\}) = \ker [i_0^{1}] \oplus \ker [i_0^{2}] \oplus \ker [i_0^{3}] = 0 \oplus 0 \oplus {\bf R}^3 = {\bf R}^3,$$ $$H_{1}(\{K^{i}\}) = \ker [i_1^{1}] \oplus \ker [i_1^{2}] \oplus \ker [i_1^{3}] = {\bf R} \oplus 0 \oplus {\bf R}^2 = {\bf R}^3 .$$
Our conclusion is: the homology group of a gray scale image is the direct sum of the kernels of the homology maps of the inclusions of its frames.
Exercise. Compute the homology group of (a) the negative and (b) the blurred version of the above image:
This approach is simple but it has a drawback. Consider this sequence of homology classes $$a_{1} \mapsto a_{2} \mapsto a_{3} \mapsto 0.$$ They are meant to represent the same feature of the original image, but the one that we chose to use in the homology of the image defined above is the last one, $a_{3}$. But this class represents the least prominent feature of the three! This issue becomes more obvious if we consider a blurred version of the image with all $256$ levels of gray present. Then we have a filtration of $256$ complexes and a sequence of $256$ homology classes: $$a_{1}\mapsto a_{2}\mapsto ... \mapsto a_{255}\mapsto a_{256} \mapsto 0.$$ The last non-zero element is to appear in $H(\{K^{i}\})$ and its contrast is just $1$. Such a contrast is simply invisible to the human eye. The best choice to capture the hole would be the class with the highest contrast, i.e., $a_{1}$.
What's behind the contrast is the life-span: the shortest for $a_{256}$ and the longest for $a_1$. Following this analogy, instead of capturing the classes about to die, this time we concentrate on the ones that are just born. Then we have: $$H(\{K^{i}\}) = < A_{1},B_{1},C_{2},a_{1},b_{1},c_{3} >.$$
While the idea of “death” is straightforward (the class goes to $0$), that of “birth” isn't. Certainly we need to exclude ones that are already alive, i.e., the ones present in the last complex. Those form the image of $i^1_*$! One can think of those left as the orthogonal complement in the linear algebra environment, $(\operatorname{Im}\,i_*^{n})^{\bot}$, or we can exclude the image via quotient: $H(K^{n})/\operatorname{Im} \, i_*^{n} $.
Special kinds of quotients like these appear in group theory. For a given homomorphism $f:G \to H$ of abelian groups, define the cokernel of $f$ as $$\operatorname{coker}f=H / \operatorname{Im} f.$$
Proposition. The following are exact sequences, with inclusions and projections unmarked: $$0 \to \operatorname{Im} f \to H \to \operatorname{coker} f \to 0,$$ $$0 \to \ker f \to G \quad\xrightarrow{\quad f \quad} \quad H \to \operatorname{coker} f \to 0.$$
As before, homology generates a system of groups and homomorphisms: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{cccccccccccccccccc} 0 & \ra{i_*^0} & H(K^{1}) & \ra{i_*^1} & H(K^{2}) & \ra{i_*^2} & ... & \ra{i_*^{s-1}} & H(K^{s}), \end{array}$$ but this time we add $0$ in the beginning, for convenience, with $i_*^0=0$.
Definition. The homology group of filtration $\{K^{n}\}$ is defined as the product of the cokernels of the inclusions: $$H(\{K^{n}\}) := \operatorname{coker} i_*^{0} \oplus \operatorname{coker} i_{*}^{1} \oplus ... \oplus \operatorname{coker} i_{*}^{s-1}.$$
Exercise. Prove that the two definitions produce isomorphic vector spaces for homology over ${\bf R}$.
Homology groups of filtrations
We have learned how to capture homology classes of a gray-scale image -- represented by a filtration -- without double counting. We now apply this approach to an arbitrary filtration: \begin{equation*} K^{1}\hookrightarrow K^{2}\hookrightarrow K^{3}\hookrightarrow ... \ \hookrightarrow K^{s}. \end{equation*} denoted by $\{K^{n}\}$. Here $K^{1},K^{2},... ,K^{s}$ are polyhedra and the arrows represent the inclusions $i^{n}:K^{n}\hookrightarrow K^{n+1}$. Next, homology generates a direct system of groups and homomorphisms: $$ H(K^{1})\to H(K^{2})\to ... \to H(K^{s}) \to 0.$$ We denote this direct system by $$\{H(K^{n})\} = \{H(K^{n}),i_*^{n}:\ n=1,2,...,s\}.$$ The zero is added in the end for convenience.
Our goal is to define a single structure that captures all homology classes in the whole filtration without double counting. We choose to concentrate on the kernels of the homology maps of the inclusions. The rationale is that if $$x\in H(K^{n}),\ y\in H(K^{n+1}),$$ $$y=i_*^{n}(x),$$ and there is no other $x$ satisfying this condition, then $x$ and $y$ may be thought of as representing the same homology class of the geometric object behind the filtration.
Definition. The homology group of filtration $\{K^{n}\}$ is defined as the direct sum of the kernels of the inclusions: $$H(\{K^{n}\}) := \ker i_*^{1}\oplus \ker i_{*}^{2}\oplus ... \oplus \ker i_{*}^{s}.$$
Here, from each group, we take only the elements that are about to die. Since each dies only once, there is no double-counting. Since everyone will die eventually, every homology class is accounted for. Therefore, each appears once and only once.
Example. Let's consider the filtration from above:
Following the definition, its homology group is: $$\begin{array}{cccccccccccccc} & \ker i_*^{1} &\oplus &\ker i_{*}^{2}&\oplus &\ker i_{*}^{3}&\oplus &\ker i_{*}^{4}&\oplus &\ker i_{*}^{5}&\oplus &\ker i_{*}^{6}\\ H_0 =&{\bf R} &\oplus &0 &\oplus &0 &\oplus &{\bf R} &\oplus &0 &\oplus &{\bf R}\\ H_1 =&0 &\oplus &0 &\oplus &{\bf R} &\oplus &0 &\oplus &{\bf R} &\oplus &0 \end{array}$$
$\square$
Exercise. Compute the homology groups for the filtrations from the previous subsections: (a) the Vietoris-Rips construction of the circle, and (b) the increasing resolution of the triangle.
Let's state a few simple facts about this group.
Proposition. If $i_*^n$ is an isomorphism for each $n=1,2,...,s-1$, then $$H(\{K^{n}\})=H(K^{1}).$$
Proposition. If $i_*^n$ is a monomorphism for each $n=1,2,...,s-1$, then $$H(\{K^{n}\})=H(K^{s}).$$
Proposition. Suppose $\{K^{n},i^{n}\}$ and $\{L^{n},j^{n}\}$ are filtrations. Then $$H(\{K^{n}\sqcup L^{n}\})=H(\{K^{n} \})\oplus H(\{L^{n}\}).$$
Exercise. Prove these propositions.
Exercise. Illustrate the propositions with examples of (a) thresholding of gray scale images, and (b) the Vietoris-Rips construction for point clouds.
Note: Any direct system of polyhedra -- not just a filtration -- will generate a direct system of groups. The above definition of the homology group will still make sense.
Maps of filtrations
What about maps? Suppose $$\{K^{n},i^{n}:\ n=1,2,...,s\} \text{ and } \{L^{n},j^{n}:\ n=1,2,...,s\}$$ are filtrations of complexes, with the same number of elements. Suppose also we have a sequence of simplicial (or cubical) maps $$f^n:K^{n} \to L^{n},\ n=1,2,...,s.$$ Since each $K^n$ is a subset of $K^s$, each $f^n$ is simply the restriction of $f^s$ to $K^n$: $$f^n=f^s\Big|_{K^n}.$$ They are well defined as long as $$f^s(K^n) \subset L^n.$$ Then such a sequence is called a filtration map. We denote this map by $$\{f^n\}:\{K^{n}\} \to \{L^{n}\}.$$
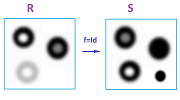
Example. What kind of function between two gray scale images generates a filtration map? Would every function $f:R\to S$ that maps the rectangle $R$ of the first image to the rectangle $S$ of the second be a filtration map? We know that $$K^n=p^{-1}(r_n,\infty),\ L^n=q^{-1}(s_n,\infty),$$ where $p:R\to {\bf R},q:S\to {\bf R}$ are the gray scale functions of the two images and $r_n,s_n\in {\bf R}$ are some thresholds. Then the condition $f(K^n) \subset L^n$ means that $qf(p^{-1}(r_n))\ge s_n$.
If we are dealing with actual digital images, the thresholds are the same: $r_n=s_n= n=0,1,...,256$. In that case, the last condition means that $f$ has to make pixels darker:
$\square$
Exercise. What kind of function between two point clouds generates a filtration map under the Vietoris-Rips construction?
Alternatively and equivalently, we require that these maps $f^n:K^{n} \to L^{n}$ commute with the inclusions: $$j^nf^n=f^{n+1}i^n,\ n=1,2,...,s-1.$$ In other words, the diagram commutes: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{cccccccccccccccccccccccc} ...& \to & K^{n} & \ra{i^n} & K^{n+1} & \to &...\\ ...& & \da{f^{n}} & & \da{f^{n+1}}& &... \\ ...& \to & L^{n} & \ra{j^n} & L^{n+1} & \to &... \end{array} $$
The advantage of this definition is that it applies to any direct system of spaces. In addition, we have another commutative diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccccc} ...& \to & H(K^{n}) & \ra{i^n_*} & H(K^{n+1}) & \to &...\\ ...& & \da{f^{n}_*} & & \da{f^{n+1}_*}& &... \\ ...& \to & H(L^{n}) & \ra{j^n_*} & H(L^{n+1}) & \to &... \end{array} $$
We are now in a familiar position; we can enhance our understanding of this new concept by taking a broader, category theory view.
Exercise. Prove that filtrations form a category with filtration maps as morphisms.
Exercise. Prove that homology is a functor from the category of filtrations to the abelian groups.
Exercise. Define the homology map $\{f_n\}_*:H(\{K^n\}) \to H(\{L^n\})$ of a filtration map $\{f_n\}:\{K^n\} \to \{L^n\}$. Compute the homology map of the filtration map in the last example.
Next, we will further develop our new construction to allow us to filter homology classes of low importance out of the homology groups.
The “sharp” homology of a gray scale image
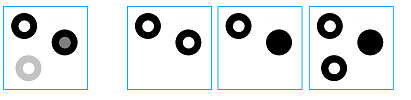
In analysis of digital images, one may need to measure the importance of topological features in terms of their contrast and discard those with low contrast as irrelevant details or simply noise:
The images below show how the number of objects detected declines as the contrast threshold increases: $0, 30, 50, 70, 125$:
How do we apply this simple idea to the homology of gray scale images of any dimension?
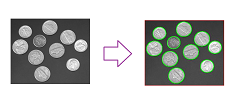
Let's take a look at the image of the rings again:
One may observe that the contrast of some of the features in the original image is lower than others. These are, in comparison to the surrounding area:
- the third ring,
- the hole in the second ring, and
- the hole in the third ring.
It is conceivable that we would classify these less prominent features as minor and choose to ignore them.
The “contrast” of an object is understood as the difference between the highest gray level adjacent to the object and the lowest gray level within the object. It is equal to the length of the object's life-span, i.e., the persistence, and as such it is fully applicable to homology classes of all dimensions.
We use the algebra of homology classes: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{#1}\!\!\!\!\!} \begin{array}{cccccccccccccccccccccc} & i_*^{1} & & i_*^{2}& & i_*^{3} \\ A_{1} & \mapsto & A_{2} & \mapsto & A_{3} & \mapsto & 0 \\ B_{1} & \mapsto & B_{2} & \mapsto & B_{3} & \mapsto & 0 \\ & & & & C_{3} & \ra{} & 0 \\ a_{1} & \mapsto & a_{2} & \mapsto & a_{3} & \mapsto & 0 \\ b_{1} & \mapsto & 0 & & & & \\ & & & & c_{3} & \mapsto & 0 \end{array} $$ Then we compute the contrast as the lengths of the life-spans of these homology classes, $P(x)$: $$\begin{matrix} P(A_{1})=3, & P(A_{2})=2, & P(A_{3})=1,\\ P(B_{1})=3, & P(B_{2})=2, & P(B_{3})=1,\\ & P(C_{2})=2, & P(C_{3})=1,\\ P(a_{1})=3, & P(a_{2})=2, & P(a_{3})=1,\\ P(b_{1})=1, & & \\ & & P(c_{3})=1. & \end{matrix}$$
We define more inclusions: $$i^{m,n}:=i^ni^{n-1}...i^m:K^m \hookrightarrow K^n,$$ for $m\le n$, in order to measure these lifespans.
Let's suppose that we are only interested in features with contrast of at least $3$ and consider the rest noise. It is easy to see the homology classes with persistence of $3$ or higher among the generators: $$A_{1},B_{1},a_{1}.$$ However, since the persistence can decrease under algebraic operations, the elements of high persistence do not, in general, form a subgroup of the respective homology group of the filtration. This is why we, first, concentrate on the classes with low persistence, i.e., the noise. In particular, the classes in $H(K^{1})$ of persistence $2$ or lower do form a group. It is, in fact, the kernel of $i_*^{2,3}$: $$\begin{array}{lllllllllllllllll} 0 & =\ker i_*^{1,3}, & <A_{2},B_{2},C_{2}> & =\ker i_*^{2,3}, & <A_{3},B_{3},C_{3}> & =\ker i_*^{3,3},\\ <b_{1}> & =\ker i_*^{1,3}, & <a_{2}> & =\ker i_*^{2,3}, & <a_{3},c_{3}> & =\ker i_*^{3,3}. \end{array}$$ We now “remove” this noise from the homology groups of the filtration by taking their quotients modulo these kernels: $$\begin{array}{llllllll} < A_{1}, B_{1} > / 0 & = < A_{1}, B_{1} >, \\ < A_{2}, B_{2}, C_{2} > / < A_{2}, B_{2}, C_{2} > & = 0, \\ < A_{3}, B_{3}, C_{3} > / < A_{3}, B_{3}, C_{3} > & = 0,\\ < a_{1}, b_{1} > / < b_{1} > & = < a_{1} >, \\ < a_{2} > / < a_{2} > & = 0, \\ < a_{3}, c_{3} > / < a_{3}, c_{3} > & = 0. \end{array}$$ The end result is the $3$-persistent homology groups of the image: $$\begin{array}{lllllllllllllllll} H_{0}^{3}(\{K^{i}\}) & = < A_{1}, B_{1} > / 0 & = < A_{1}, B_{1} >, \\ H_{1}^{3}(\{K^{i}\}) & = < a_{1}, b_{1} > / < b_{1} > & = <a_{1} >. \end{array}$$
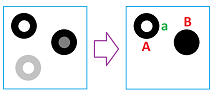
Observe that the output is identical to the homology of a single complex, i.e., a binary image, with two components and one hole:
It is a “sharpened” version of the original, similar to what we see in image enhancement applications:
The persistent homology group of a gray-scale image captures only its topology. Indeed, observe:
- the holes in the second and third rings have the same persistence (the contrast) and, therefore, occupy the same position in the homology group regardless of their birth dates (the gray level);
- if we shrunk or stretched one of these rings, its persistence and, therefore, its place in the homology group wouldn't change.
Meanwhile, in the Vietoris-Rips construction, the persistence, i.e., the number $death - birth$, of a homology class does contain information about the size of the cycles representing this class. For example, a set of points arranged in a circle will produce a $1$-cycle with twice as large birth, death, and persistence than the same set shrunk by a factor of $2$. One can then define the persistence via division instead, as $death/birth$, in order to have the desired property of scale independence. The same result can be achieved by an appropriate re-parametrization of the filtration.
Exercise. Compute the $p$-persistent homology groups of (a) the blurred version and (b) the negative of the image of rings, for various values of $p$.
Persistent homology groups of filtrations
In the general context of filtrations, the measure of importance of a homology class is its persistence which is the length of its lifespan within the direct system of homology of the filtration: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{ccccccccccccc} H(K^{1}) & \ra{i_*^1} & H(K^{2}) & \ra{i_*^2} & ... & \ra{i_*^{s-1}} & H(K^{s}) & \to 0. \end{array}$$
Definition. We say that the persistence $P(x)$ of $x\in H(K^{n}),\ n=1,2,...,$ is equal to $p$ if
- $i_*^{n,n+p}(x)=0$, and
- $i_*^{n,n+p-1}(x)\neq 0.$
Our interest is in the “robust” homology classes, i.e., the ones with high persistence. However, the set of all of these classes is not a group as it doesn't even contain $0$. Therefore we have to deal with “noise” first.
Definition. Given a positive integer $p$, the $p$-weak homology group $\mathring{H}^{p}(\{K^{n}\})$ of filtration $\{K^{n}\}$ is the group of all elements of $H(\{K^{n}\})$ with persistence less than $p$.
This means that for every $x\in H(K^n),\ n=1,2...$, we have: $$x\in \mathring{H}^{p}(\{K^{n}\}) \Leftrightarrow i_*^{n,n+p-1}(x)= 0.$$
Next, we remove the noise from the homology group. Just as in the noiseless case we started with, we define a single structure to capture all (robust) homology classes.
Definition. The $p$-persistent homology group of $\{K^{n}\}$ is defined as $$H^{p}(\{K^{n}\}) := H(\{K^{n}\}) / \mathring{H}^{p}(\{K^{n}\}).$$
The meaning of this definition is that, if the difference between two homology classes is deemed noise, they should be equivalent.
Note: The way persistence is defined ensures that we can never end up with the "Cheshire cat of topology" by removing a component as noise but keeping a hole in it.
We next explore how this definition applies to each complex of the filtration. Suppose a positive integer $p$ is given. For each complex $K^n$, we can think of its $p$-weak homology group $\mathring{H}^{p}(K^{n})$ as the group of all elements of $H(K^{n})$ with persistence less than $p$: $$\mathring{H}^{p}(K^{n}) := \ker i_*^{n,n+p-1}.$$ Suppose $$x \in \mathring{H}^{p}(K^{n})\subset H(K^n).$$ Let $y=i_*^{n,n+1}(x) \in H(K^{n+1})$. What is its persistence? Let's compute: \begin{eqnarray*} i_*^{n+1,n+1+p}(y) & = & i_*^{n+1,n+1+p}(i_*^{n,n+1}(x)) \\ & = & i_*^{n,n+1+p}(x) = i_*^{n+p,n+p+1}(i_*^{n,n+p}(x)) \\ & = & i_*^{n+p,n+p+1}(0) = 0. \end{eqnarray*} Hence $y\in \ker i_*^{n+1,n+1+p}=\mathring{H}^{p}(K^{n+1}).$ We have proved that the homomorphism $$i_*^{n,n+1}:\mathring{H}^{p}(K^{n}) \to \mathring{H}^{p}(K^{n+1}),$$ as the restriction of the homology map of the inclusion, is well-defined.
Therefore, we have a new direct system: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{cccccccccc} \mathring{H}(K^{1}) & \ra{i_*^1} & \mathring{H}(K^{2}) & \ra{i_*^2} & ... & \ra{i_*^{s-1}} & \mathring{H}(K^{s}) & \to 0. \end{array}$$
Exercise. Prove these identities: $$\begin{array}{llllllllll} \mathring{H}^{p}(\{K^{n}\}) &= \mathring{H}^{p}(K^{1}) &\oplus &... &\oplus& \mathring{H}^{p}(K^{s}), \\ H^{p}(\{K^{n}\}) &= \left( H(K^{1}) / \mathring{H}^{p}(K^{1}) \right) &\oplus& ... &\oplus& \left( H(K^{1}) / \mathring{H}^{p}(K^{s}) \right). \end{array}$$
Exercise. State and prove the properties of $H^{p}(\{K^{n}\})$ analogous to the ones of $H(\{K^{n}\})$.
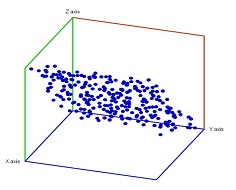
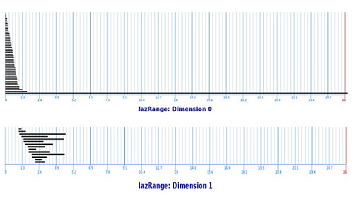
Example. We consider next an example of computing the persistent homology of a point cloud with homology software called JPlex. Here, noise has been added to a point cloud of the plane in space:
Let's see if we can recover the topology of the underlying data.
A filtration is built via the Vietoris-Rips construction. Next, JPlex provides us with the life-spans of the cycles:
We can see the following:
- There is one cycle in dimension $0$ that has a much longer lifespan than others. So, the set is probably path-connected!
- In dimension $1$, no single cycle persists significantly. So it's probably simply connected!
In addition to these global topological characteristics of the complex, homology theory can also provide local information. For every small patch $P$ of $K$, we can compute the “local” homology by, essentially, collapsing the complement of $P$ to a single point. Then, if $K$ is a manifold, its dimension is equal to $n$ provided this homology is non-trivial only in dimension $n$.
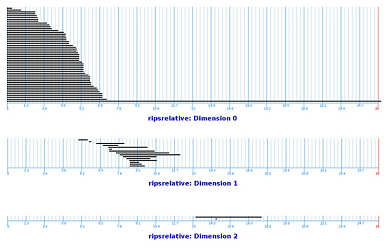
These are the life-spans of the relative cycles of our filtration:
This is what we see:
- In dimension $0$, one cycle persists longer that other $0$-cycles.
- In dimension $1$, no single cycle has a particularly long life-span compared to other $1$-cycles.
- In dimension $2$, one cycle has a significant life-span.
Based on this data, we determine the dimension of our data set. We discard the low persistence homology classes, and what's left give us the persistent Betti numbers as the dimensions of the persistent homology groups: $$\beta_0 = 1, \beta_1 = 0, \beta_2 = 0, ...$$ Thus, the dataset has a single component and no other topological features. Next, the local Betti numbers are: $$\beta_0 = 1, \beta_1 = 0, \beta_2 = 1, \beta_3 = 0, ...$$ The result confirms that the data set is two-dimensional, i.e., a surface.
$\square$
Other instances of parametric spaces
We have seen three main instances of parametric complexes in this section:
- the Vietoris-Rips construction for a point cloud,
- the thresholding of a gray scale image, and
- creating a binary image of an object with increasing resolution.
Gray scale images are a very convenient target for demonstrating the power of persistence as a way to handle uncertainty. In terms of complexity, they lie between binary and color images.
There is no uncertainty in binary images similar to the one associated with the presence of gray levels as each pixel is either black or white. However, we have already seen that switching the value of a single pixel could dramatically change the topology of the image. When this happens, we can say that the topological features that have appeared or disappeared aren't robust, or they have low persistence.
A general approach to this issue is via the so-called “morphological operations”, the nature of which is geometrical:
- dilation makes black each pixel adjacent to black, while
- erosion makes white each pixel adjacent to white.
Thus, dilation and erosion expand and shrink objects in a binary image, respectively. Then the robustness of the topological features of the image can be measured in term of how many dilations and erosions it takes to make it disappear. It is clear that repeating dilations will produce a filtration while erosion produces a revered filtration. Therefore, the robustness described above is just another example of persistence!
These are the types of questions we would answer:
- how many erosions does it take to split a component into two or more or make it disappear?
- how many dilations does it take to create a hole in a component or merge two components?
- etc.
For example, these are some typical observations:
- a component separated from others will have higher persistence under dilation that one with close neighbors; or
- a round component will have higher persistence under erosion than an elongated one.
Exercise. Make the above statements precise and prove them.
Exercise. Define filtrations and persistence for a continuous parameter, $t\in [0,1]$. What would dilation/erosion filtrations look like?
Exercise. Suppose four individuals, $A,B,C,D$, visited four stores: Kroger, Macy's, JCPenney, and Walmart. Suppose they also rated the stores with numbers between $1$ and $4$: $$\begin{array}{c|cccccc} & K &M &J &W \\ \hline A: &1 &2 &3 &4\\ B: &1 &1 &1 &1 \\ C: &4 &4 &1 &1\\ D: &3 &2 &2 &1 \end{array}$$ Construct a filtration of simplicial complexes based on these ratings and compute the persistence.
Exercise. Starting with a point cloud, define a filtration based on the density of its points:
Multiple parameters
The color effect in color images is produced by combining different levels of the “primary colors”: red, green, and blue (RGB). Just as the gray in gray scale images, the values of each primary color runs from $0$ to $255$. Thus, in an RGB image, to every pixel there are assigned $3$ integers. One can think of a color image as a $3$-vector attached to each pixel, or as $3$ tables of integers, or $3$ gray scale images, etc.
What we have learned from our analysis of gray scale images is that we should break this parametric image into binary ones.
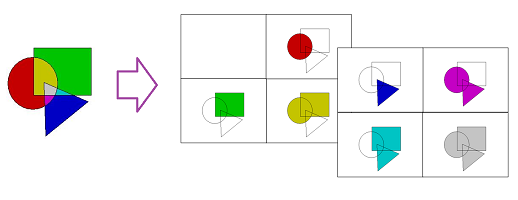
Example. Below, we present a simplified case when there are only $2$ levels of each of the three primary colors. The image is represented by an array of $8$ binary images (they are colored for convenience):
This array is a filtration with inclusions that go: from left to right, from top to bottom, and from the lower level to the top level. Then we conclude that, without double-counting, there is only one component in the image. This seemingly counter-intuitive conclusion is justified as follows: yes, there are three clearly visible objects in the image, but they overlap!
$\square$
In the general case, we, by means of a procedure similar to thresholding described above, represent a color image as an array of binary images. The “color space” is a $255 \times 255 \times 255$ array with each entry corresponding to a particular color. This is a strip from this space:
Therefore, thresholding a color image will produce a $255 \times 255 \times 255$ array of binary images.
Exercise. Give a precise description of this thresholding procedure.
The property that this array satisfies is important: when the value of any of the primary color increases, the binary image grows. As a result, the array is also equipped with inclusions connecting these binary images. Together these complexes and maps form a $3$-dimensional commutative diagram and so do their homology groups and homology maps.
One layer of this filtration, as well as its homology, is shown below with all arrows representing inclusions. Both diagrams are commutative: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{ccccccccccccccccc} K^{0,0} & \ra{i} & K^{1,0} & \ra{i} & K^{2,0} & \ra{i} & ... && H(K^{0,0}) & \ra{i_*} & H(K^{1,0}) & \ra{i_*} & H(K^{2,0}) & \ra{i_*} &...\\ \da{i} & & \da{i} & & \da{i} & & ... && \da{i_*} & & \da{i_*} & & \da{i_*} \\ K^{0,1} & \ra{i} & K^{1,1} & \ra{i} & K^{2,1} & \ra{i} & ... && H(K^{0,1}) & \ra{i_*} & H(K^{1,1}) & \ra{i_*} & H(K^{2,1}) & \ra{i_*} &...\\ \da{i} & & \da{i} & & \da{i} & & ... && \da{i_*} & & \da{i_*} & & \da{i_*} \\ K^{0,2} & \ra{i} & K^{1,2} & \ra{i} & K^{2,2} & \ra{i} & ... && H(K^{0,2}) & \ra{i_*} & H(K^{1,2}) & \ra{i_*} & H(K^{2,2}) & \ra{i_*} &...\\ \da{i} & & \da{i} & & \da{i} & & ... && \da{i_*} & & \da{i_*} & & \da{i_*} \\ .. & .. & .. & .. &.. & .. & ... && .. & .. & .. & .. & .. & ...\\ \end{array}$$
Exercise. Draw the rest of the diagram.
We can call this a multi-parameter filtration.
What is the homology group of such an image? As before, we look at the kernels of the homology maps of the inclusions. We want to capture for each element of the filtration its homology classes that are about to die (the zero group is added at the end as before). There are three inclusions for each and we take the intersection of these three kernels in order to make sure we are including only the homology classes that won't reappear elsewhere. Finally, the homology group of the color image is the direct sum of these intersections over all elements of the filtration.
Exercise. Find the homology group of this color image and the one above:
Exercise. Prove that a gray scale image analyzed as a color image will have the same homology group as before.
Besides color images, multi-parameter filtrations may come from combinations of what we have seen above: the erosion-dilation of gray scale images, or the Vietoris-Rips construction for gray scale images, etc.
It is just as easy, however, to develop homology in an even more general setting. A direct system $\{K^{n}\}=\{K^{n}:n\in Q\}$ is a collection of sets indexed by a partially ordered set $Q$ so that if $n < m$ then there is a function $$i^{nm}:K^{n}\to K^{m}.$$ When these sets are complexes and the functions are simplicial or cubical maps, homology creates a new direct system, of groups and homomorphisms: $$i_*^{nm}:H(K^{n})\to H(K^{m}), \ n<m.$$ For convenience, we add a maximal element $X=0$ to this direct system. As before, the goal is to capture all homology classes of the filtration, without repetition. We define the homology group of the direct system $\{K^{n}\}$ as $$H(\{K^{n}\}) = {\displaystyle\bigoplus\limits_{n}}{\displaystyle\bigcap \limits_{m>n}} \ker i_*^{nm} .$$ The analogs of the results about the single parameter filtrations hold.
Exercise. Show that this definition generalizes the previous one.
Exercise. Define persistence in the multi-parameter setting. Hint: Beware of the "Cheshire cat"!
Exercise. Compare the above construction to the following. Given a direct system of groups and homomorphisms: $$\{A^{n}\}=\{A^{n},j^{nm}:A^{n}\to A^{m}| \ n,m\in Q, n<m\},$$ the direct limit of this system is the group $$\lim _{\rightarrow}\{A^n\}:=\bigoplus_n A^n / _{\sim},$$ where $$x_n\sim x_m \Leftrightarrow j^{nq}(x_n)=j^{mq}(x_m), \text{ for some } q\in Q.$$