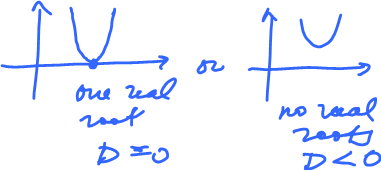Inner product spaces: part 1

Distances and angles in vector spaces

Algebra only, until now. By that I mean that we did a lot of computations with vectors.

What about measurement? That's geometry!

Note there is no measuring in a vector space. But, in that case, there are no distances, no limits, no calculus...

Plan: Take a vector space and equip it with extra structure, so that we can measure.

To understand how, let's observe that we do measure in ${\bf R}^1$, ${\bf R}^2$, ${\bf R}^3$, etc. How?

Consider the distance formula in ${\bf R}^2$.

Which is $$d=\sqrt{(a-u)^2+(b-v)^2},$$ that comes from Pythagorean Theorem.

In ${\bf R}^3$ also:

we have $$D=\sqrt{(a-u)^2+(b-v)^2+(c-w)^2}$$ etc.

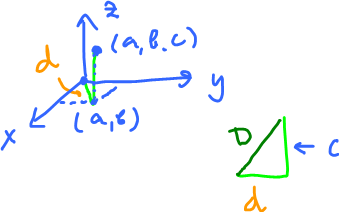
Then, the distance from $d=(a,b)$ to $0$ is $\sqrt{a^2+b^2}$. $$D^2=d^2+c^2 = a^2+b^2+c^2,$$ diagonal of box $a \times b \times c$.

In ${\bf R}^n$ distance formula is the following.

The distance between $a=(a_1,\ldots,a_n)$ and $b=(b_1,\ldots,b_n)$ is $$d(a,b)=\sqrt{(a_1-b_1)^2+\ldots+(a_n-b_n)^2}.$$ (it's a number!)

We can measure vectors and, therefore, can consider convergence:

• given $x_i \in {\bf R}^n$, $x_i \rightarrow a \in {\bf R}^n$ if distance from $x_i$ to $a$ goes to $0$ as $i \rightarrow \infty$, i.e.,

$$\displaystyle\lim_{i \rightarrow \infty} d(x_i,a)=0.$$

With this you can introduce limits, continuity, derivative, integral, the rest of calculus. So, we have calculus in ${\bf R}^n$ (not just ${\bf R}^3$ as in calc 3). It's called vector calculus.

Question: What about other vector spaces? Especially infinite dimensional ones such as ${\bf F}([a,b])$.

Further: What's the distance between $f$ and $g$, two functions?

Possible answer: Assume $f,g$ continuous. Then define: $$d(f,g)=\displaystyle\int_a^b(f-g)^2 dx$$ or $$\displaystyle\int_a^b|f-g|dx.$$ This is the area between the graphs of $f$ and $g$:

.

Another measurement in the Euclidean space is angles.

Suppose we have $u,v \in {\bf R}^2$, so that $u=(u_1,u_2), v=(v_1,v_2)$.

Known formula: $$\cos \alpha=\frac{u_1v_1+u_2v_2}{\sqrt{u_1^2+u_2^2}\sqrt{v_1^2+v_2^2}}.$$ Here we identify the top to be the dot product of $u,v \in {\bf R}^2$ and the bottom is the norms of $u$ and $v$.

It is better notation then: $$= \frac{ < u,v > } {\lVert u \rVert \lVert v \rVert}.$$ Observation: no mention of dimension!

But does the angle between two vectors even make sense in ${\bf R}^n$?

Given $u,v \in {\bf R}^n$, what is the meaning of "the angle between vectors"?

First, we know what it is in ${\bf R}^2$.

Now, consider ${\bf R}^3$.

In ${\bf R}^3$, we make a plane $P={\rm span}\{u,v\}$ (the dimension is 2, a plane). Then we can measure the angle between these vectors -- within $P$!

Similar for ${\bf R}^n$.

Spaces of functions

Back to functions. Why do we even care about distances between them?

Suppose we want to approximate ${\rm sin}$ at $0$ (calc 2)?

Its Taylor polynomial of degree $3$ is $$T_3(x)=x-\frac{x^3}{3!}.$$

That's fine but very superficial.

Bird's eye view: ${\bf P}^3$ is a subspace of $C[a,b]$!

Observations:

• 1. We want to find the nearest point to $\sin$ in ${\bf P}^3$. (That's $T_3$.)

This is why we need to be able to measure distances.

• 2. The segment from ${\rm sin}$ to ${\bf P}^3$ should be perpendicular to ${\bf P}^3$, i.e. $\sin - T_3 \perp T_3$.

This is why we need to be able to measure angles.

That was an introduction to analysis in $C[a,b]$.

What's missing now is an analog of the dot product.

Define $<f,g>$, the "inner product" on $C[a,b]$ as follows: $<f,g> = \displaystyle\int_a^b fg dx$.

Note: Compare $\displaystyle\int_a^b fg dx$ versus $\displaystyle\sum_{i=1}^n a_ib_i$.

• In the first we multiple value-wise and integrate, and
• in the second we multiply coordinate-wise and add.

Very similar...

Evaluate: $$<\sin,\cos> = \displaystyle\int_0^{\pi} \sin x \cos x dx = \displaystyle\int_0^{\pi} \frac{1}{2}\sin 2x dx = 0.$$ Since $\sin 2x$ is $\pi$-periodic.

So $\sin \perp \cos$, orthogonal.

Now, we want to define the inner product, for an abstract vectors pace, via axioms.

Inner product spaces

Given a vector space $V$, an inner product on $V$ is a function that associates a number to each pair of vectors in $V$: $V \ni u,v \rightarrow < u,v > $, that satisfies these properties:

• 1. $<v,v> \geq 0$ for any $v \in V$ (called the norm of $v$). Also $<v,v>=0$ if and only if $v=0$ -- positive definite law.
• 2. $ < u , v > = <v,u> $ -- commutativity law;
• 3. $ <ru,v>=r < u ,v> $ -- homogeneity law;
• 4. $ < u + u ' ,v>=< u ,v>+< u ' ,v> $ -- distributive law;

Note: 3. and 4. together make up linearity.

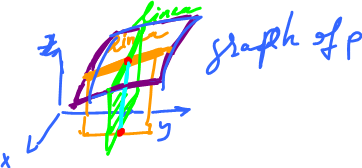
Consider $p \colon V \times V \rightarrow {\bf R}$, where $p ( u , v)= < u , v>$.

Then 3 and 4 is linearity of $p$ with respect to the first variable, and the second variable, separately:

• 1) Fix $v=b$, then $p(u,b)$ is linear: $V \rightarrow {\bf R}$.
• 2) Fix $u=a$, then $p(a,v)$ is linear: $V \rightarrow {\bf R}$.

But is $p \colon V \times V \rightarrow {\bf R}$ a linear function?

Graphically, these two observations can be illustrated as follows.

Let $V={\bf R}$, $p \colon {\bf R}^2 \rightarrow {\bf R}$.

The intersections of the graph with planes parallel to the $xz$-plane, or $yz$-plane, are straight lines.

Question: Is the graph a plane?

No.

On $R$, $p(x,y)=xy$, while linear has the form $Ax+By$. This is plane vs saddle:

Such a function is called bi-linear.

Let's verify the axioms for the dot product.

The dot product is defined on ${\bf R}^n$: $$u=(u_1,\ldots,u_n), v=(v_1,\ldots,v_n) \in {\bf R}^n$$ then $$< u , v>=u_1v_1 + u_2v_2 + \ldots + u_nv_n.$$ This is coordinate-wise multiplication followed by addition.

Axioms:

1. First, $$< u, u> = u_1^2 + \ldots + u_n^2 \geq 0,$$ of course. Also, if $$< u, u> = u_1^2 + \ldots + u_n^2 = 0,$$ i.e., the sum of non-negative numbers is zero, then so is each of them: $$u_1^2=\ldots=u_n^2=0 \Rightarrow u_1=\ldots=u_n=0 \Rightarrow u=0.$$

2. This is easy: $$< u ,v> = u_1v_1 + \ldots + u_nv_n = v_1u_1 + \ldots + v_nu_n = <v , u >.$$

3. And so is this:

$\begin{array}{} < u+u',v> &= (u_1+u_1')v_1 + \ldots + (u_n+u_n')v_n \\ &= u_1v_1 + u_1'v_1 + \ldots + u_nv_n + u_n'v_n \\ &=(u_1v_1+\ldots+u_nv_n)+(u_1'v_1+\ldots+u_n'v_n) \\ &= < u ,v> + < u ' ,v>. \end{array}$

4. Similarly:

$\begin{array}{} <r u , v> &= (ru_1)v_1 + \ldots + (ru_n)v_n \\ &= r(u_1,v_1) + \ldots + r(u_n,v_n) \\ &= r(u_1v_1 + \ldots + u_nv_n) \\ &= r < u , v>. \end{array}$.

We used here the corresponding properties of real numbers, especially multiplication (which is the dot product on ${\bf R}$ after all).

Conclusion: the dot product is an inner product on ${\bf R}^n$.

What about inner product on the space of continuous functions $C[a,b]$? $b >a$

Definition: $$<f,g> = \displaystyle\int_a^b fg.$$ (same as $\displaystyle\int_a^b f(x)g(x) dx$)

Axioms:

• 1. $\displaystyle\int_a^b f^2 \geq 0$ ;

Use a calc 1 theorem here.

• 2. $\displaystyle\int_a^b fg = \displaystyle\int_a^b gf$;
• 3. $\displaystyle\int_a^b (f+g)h = \displaystyle\int_a^b(fh+gh) = \displaystyle\int_a^b fh + \displaystyle\int_a^b gh$;
• 4. Same.

Numbers 3. and 4. come from linearity of the integral.

Follow from the axioms:

Properties:

• 1. $<v,0> = <0,v> = 0$;
• 2. $<v,ru>=r<v, u > \Leftarrow$ (2) and (4);
• 3. $<v,u+u'>=<v, u >+<v, u ' > \Leftarrow$ (2) and (3).

Items2. and 3. are linearity with respect to the second variable.

The norm

Definition: Given an inner product space $V$, then the norm of $V$ is the function given by $\lVert v \rVert = \sqrt{<v,v>}, v \in V$.

You can think of it as a function $n \colon V \rightarrow {\bf R}^+$.

Properties:

• 1. From Axiom 1, $\lVert v \rVert^2 = <v,v> \geq 0$ and $\lVert v \rVert = 0$ if and only if $v = 0$. It is positive definite.
• 2. From Axiom 3, $\lVert rv \rVert ^2 = <rv, rv> = r^2 <v,v> = r^2 \lVert v \rVert ^2$ then $\lVert rv \rVert = |r| \lVert v \rVert$. This is "positive" homoegeneity.
• 3. From Axiom 4, $\lVert u + v \rVert \leq \lVert u \rVert + \lVert v \rVert$. This is the triangle inequality.

Sum of two sides of triangle is larger than the other side. (Proof later)

In ${\bf R}^n$, $\lVert u \rVert$ is themagnitude of $u$ (the length of the vector).

In $C[a,b]$, $\lVert u \rVert = \sqrt{\displaystyle\int_a^b u^2}$, also the magnitude, in a sense.

We can also use these three properties as axioms of the norm.

Given a vector space $V$, the norm of $V$ is a function from $V$ to ${\bf R}$ if it satisfies

• 1. $\lVert v \rVert \geq 0$ for all $v \in V$, $\lVert v \rVert = 0$ if and only if $v=0$;
• 2. $\lVert rv \rVert = |r| \lVert V \rVert$ for all $v \in V$;
• 3. $\lVert u + v \rVert \leq \lVert u \rVert + \lVert v \rVert$ for all $u, v \in V$.

Two options:

1. vector space equipped with $ < u ,v>$ or
2. vector space equipped with $\lVert u \rVert$.

And we can get 2. from 1. The latter is called a normed space.

Property: Using Axiom 4: $$ \lVert u + v \rVert ^2 = < u+v ,u +v>$$ $$=< u , u > + < v , u > + < u , v> + <v,v>$$ Using Axiom 2: $$ = \lVert u \rVert ^2 + 2< u , v> + \lVert v \rVert ^2.$$

Example: Prove that this is a scalar product on ${\bf R}^2$: $$<(x,y),(a,b)> = 2xa + 3yb$$ (in ${\bf R}^2$ the standard one is $xa + yb$).

Axiom 3: $\begin{array}{} <(x,y)+(x',y'),(a,b)> &= <(x+x',y+y'),(a,b) > \\ &\stackrel { { \rm def } } {=} g(x+x')a + 3(y+y')b> \\ &= 2xa + 2x'a + 3yb + 3y'b \\ &= (2xa+3yb) + (2x'a+3y'b) \\ &\stackrel { { \rm def } } {=} <(x,y),(a,b)>+<(x',y'),(a,b)> \end{array}$

Exercise: $V = $ sequences, define an inner product on $V$.

From the law of cosines, it follows

Theorem: In ${\bf R}^2$, the angle between vectors $u$ and $v$ satisfies $$\cos \alpha = \frac{< u , v>}{\lVert u \rVert \lVert v \rVert}.$$

If $u,v \in V$, an inner product space, and $u,v$ aren't multiples of each other, then ${\rm span}\{u,v\} = {\bf R}^2$, a plane.

Then we can apply the theorem.

Sidenote: Question, is $< u ,v>$ preserved under isomorphisms? Answer: No. We'd need what we call "isomorphisms of inner product spaces".

In particular, if the angle is $\frac{\pi}{2}$, $u,v$ are called orthogonal. It holds when $< u ,v>=0$.

Our interest will be orthogonal bases.

In particular, the standard basis $e_1,\ldots,e_n$ in ${\bf R}^n$ is orthogonal. Indeed $$<e_i,e_j> = <(0,\ldots,1,\ldots,0),(0,\ldots,1,\ldots,0)> $$ with 1's at i-th and j-th positions respectively... $$= 0 \cdot 0 + 1 \cdot 0 + \ldots + 0 \cdot 1 + \ldots + 0 \cdot 0 = 0.$$

Moreover, the basis is orthonormal, i.e., the vectors are unit vectors, $\lVert e_i \rVert = 1$.

Note: even such a special basis is not unique: try $\{-e_1, -e_2, \ldots, -e_n \}$.

Example: We can prove this: $\sin \perp \cos$ in $C[-\pi,\pi]$ and $\lVert \sin \rVert = \displaystyle\int_{-\pi}^{\pi} \sin^2xdx \neq 1$.

Also, there is another norm on $C[a,b]$: $\lVert f \rVert = \displaystyle\max_{x \in [a,b]} |f(x)|$. It's just as good...

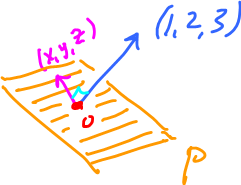
Problem: Find all vectors perpendicular to $(1,2,3)$ in ${\bf R}^3$.

Rewrite this as $<(x,y,z),(1,2,3)>=0$, find all $x,y,z$. It's the same as: $x+2y+3z=0$. This is a plane $P$:

It happens to be a subspace.

Cauchy-Schwarz inequality

Theorem. In an inner product space: $$|< u , v>| \leq \lVert u \rVert \cdot \lVert v \rVert.$$

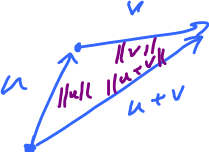
• The left hand side is the area of the parallelogram spanned by $u,v$:

• The right hand side is the area of the rectangle:

Here $u$ is turned to make $90^o$ with $v$.

So, the rectangle is taller, same base, hence larger area:

$P={\rm base}\cdot{\rm height} = \lVert v \rVert \cdot h \leq \lVert v \rVert \cdot \lVert u \rVert$

and

$R = {\rm base} \cdot {\rm height} = \lVert u \rVert \cdot \lVert v \rVert$.

Proof: A "magical" (not insightful) kind.

Consider the quadratic polynomial of $t$: $$p(t)=(u+tv)^2 = \lVert u \rVert ^2 + 2< u , v>t + \lVert v \rVert ^2 t^2.$$ Set $c=\lVert u \rVert ^2, $b = 2 < u , v>$, and $a=\lVert v \rVert^2$.

The left hand side is a perfect square, so $p(t) \geq 0$.

What does it tell us about the discriminant of the polynomial?

Well, $p \geq 0$ implies $p$ has at most one real root!

So what?

Consider $x = \frac{-b \pm \sqrt{D}}{2a}$. Plus-minus gives us two values! Unless...

...$D \leq 0$!

Compute $$D = b^2 - 4ac $$ $$= (2< u , v>)^2 - 4 \lVert v \rVert ^2 \cdot \lVert u \rVert ^2 $$ $$= 4(< u , v>^2 - \lVert v \rVert ^2 \lVert u \rVert ^2) $$ $$\leq 0.$$ So $$< u , v>^2 \leq \lVert v \rVert ^2 \lVert u \rVert ^2,$$ or $$|< u , v>| \leq \lVert v \rVert \lVert u \rVert.$$ $\blacksquare$

Let's prove that Cauchy-Schwarz inequality implies the triangle inequality: $CS \rightarrow TI$.

We want: $|< u , v>| \leq \lVert u \rVert \cdot \lVert v \rVert \stackrel{?}{\Rightarrow} \lVert x + y \rVert \leq \lVert x \rVert + \lVert y \rVert$.

Recall $\lVert u \rVert ^2 = < u , u >$, by definition.

$$\begin{array}{} \lVert x + y \rVert ^2 &= <x+y,x+y> \\ &\stackrel{distr.}{=} <x,x> + <y,x> + <x,y> + <y,y> \\ &\stackrel{def \hspace{3pt} \lVert \rVert}{=} \lVert x \rVert ^2 + 2<x,y> + \lVert y \rVert ^2 \\ &\stackrel{CS}{\leq} \lVert x \rVert ^2 + 2 \lVert x \rVert \lVert y \rVert + \lVert y \rVert ^2 \\ &= (\lVert x \rVert + \lVert y \rVert )^2 \end{array},$$ because it's a binomial. So, the triangle inequality follows. $\blacksquare$

So, the norm is well defined. In the following sense: the norm defined as $<x,x>$ in an inner product space satisfies the axioms of a normed space.