This site is being phased out.
Neighborhoods and topologies
Contents
Bases of neighborhoods
Let's recall our main definition.
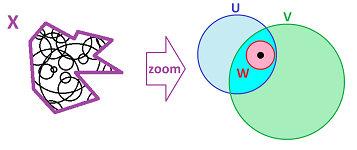
Definition. Suppose $X$ is any set. A collection $\gamma$ of subsets of $X$ satisfying the properties of:
- (B1) Covering: $\cup \gamma = X$; and
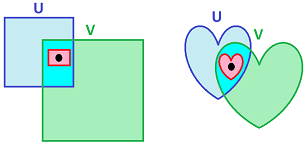
- (B2) Refining: for any neighborhoods $U, V\in \gamma$ and any point $x\in U\cap V$ in their intersection, there is a neighborhood $W\in \gamma$ of $x$ such that $W \subset U \cap V$;
is called a basis of neighborhoods in $X$. The elements of $\gamma$ are called neighborhoods, and if $x \in W \in \gamma$, we say that $W$ is a neighborhood of $x$. We commonly use $W_x$ to emphasize this.
The purpose of this definition is to enable us to discuss continuity of functions in the most general setting. Indeed, $X$ doesn't have to have either algebraic (such a vector space) or geometric (such as a metric space) structure.
In the case of the $1$-dimensional Euclidean space ${\bf R}$, our neighborhoods $\gamma$ have been simply open intervals, which makes the refining condition of $\gamma$ especially short: $$(a,b),(c,d) \in \gamma, a<c<x<b<d \Rightarrow x\in (a,b)\cap (c,d) =(c,b)\in \gamma.$$
Now, we can modify this collection $\gamma$ by choosing open intervals with the end-points:
- only rational, or
- only irrational, or
- left rational and right irrational, etc.
The proof of the refining condition above won't change!
However, closed intervals (of non-zero length) won't work: $$[a,b],[b,c] \in \gamma, a<b<c \Rightarrow [a,b]\cap [b,c] =\{b\}\not\in \gamma.$$
Another basis in ${\bf R}$ is the rays $R(s)= \{u \colon u > s \}$. Indeed, we have: $$(a,\infty),(c,\infty) \in \gamma, a<c \Rightarrow (a,\infty)\cap (c,\infty) =(c,\infty)\in \gamma.$$
Exercise. Find more examples of $\gamma$ for the line that satisfy (B1) but not (B2). Hint: try to narrow the choice of the possible centers.
Exercise. Prove that the collection of all open arcs is a basis of the circle.
The collection of all open balls in $X = {\bf R}^n$: $$\gamma_b = \{B(a, \delta): a \in {\bf R}^n, \delta > 0 \},$$ where $$B(p,d)= \{u : ||u-p|| < d \},$$ is a basis.
We will call this the standard Euclidean basis.
What are other bases in ${\bf R}^n$?
An important example is the squares. The collection of all squares (with sides parallel to the axes) in ${\bf R}^2$ is: $$\gamma_s = \{S((a,b),d) :\ (a,b) \in {\bf R}^2, d>0 \},$$ where $$S((a,b),d) = \{(x,y) :\ |x-a| < d, |y-b| < d \},$$ is a basis:
Exercise. Prove this statement. Hint: you have to be specific.
Exercise. Is the collection of all rectangles (with sides parallel to the axes) in ${\bf R}^2$ a basis? What is its analog in ${\bf R}^n$? Hint: “boxes”.
The collection of closed balls, $$\bar{B}(p,d)= \{u \colon ||u-p|| \leq d \}, d>0,$$ however is not a basis. It is easy to see if we observe that two closed balls may intersect by a single point, which is not a closed ball. If we wanted to make this collection into a basis, we'd have to add all singletons, i.e., the one-point sets, to the collection. Since those are simply balls of diameter $0$, we end up with $$\gamma_p = \{B(a, \delta) :\ a \in {\bf R}^n, \delta \geq 0 \}.$$
Exercise. Prove that this is a basis.
The sets of all:
- rectangles,
- ellipses,
- stars, etc.,
are also bases.
Exercise. Prove that disks with rational centers and/or radii form a basis.
Example. Suppose we have a parametric curve $p:{\bf R} \to {\bf R}^2$ in the plane without self-intersections. Then the image of the curve $$\operatorname{Im}(p):=\{p(t):\ t\in {\bf R} \}$$ will acquire a basis from the standard basis of ${\bf R}$, as follows. Let $$\gamma :=\{ p\left( (a,b) \right),\ a < b \}.$$
$\square$
Exercise. Provide a similar construction for parametric surfaces. What happens to these bases if there are self-intersections? What difference does continuity make?
Open sets
Below, we assume that $\gamma$ is fixed.
Now we define open sets as the ones where every point has its own neighborhood:
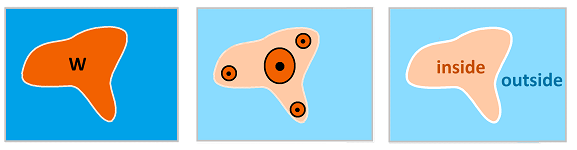
Definition. A subset $W$ of $X$ is called open (with respect to a given basis of neighborhoods $\gamma$) if for any $x\in W$ there is a neighborhood $U\in \gamma$ of $x$ that lies entirely within $W$: $$x\in U \subset W.$$
For example all “open” balls and “open” squares are open.
Exercise. What sets are open with respect to the set of all right rays?
Theorem. The intersection of two open sets is open.
We start with some analysis. We will need to write the definition three times for each of the three sets involved.
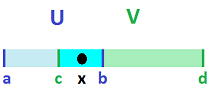
Suppose $U,V$ are open with respect to $\gamma$ and let $W:=U \cap V$. Suppose $x\in W$ is given.
Now, since $W=U\cap V$, we have $$x\in U \text{ and } x\in V.$$ Since both $U$ and $V$ are open, we conclude from the definition: $$x\in N \subset U \text{ and } x\in N \subset V.$$ Can we conclude that $$x\in N \subset U\cap V=W?$$ No! The flaw in this argument is that, applied separately, the definition produce two different $N$s!
Fortunately, the refining condition (B2) will give us the desired -- smaller -- neighborhood of $x$.
We are now prepared to write the proof.
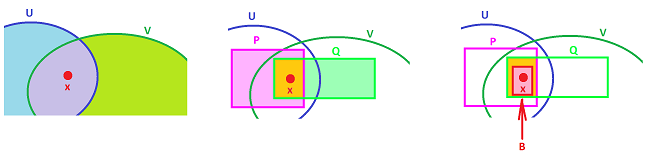
Proof. Given $x\in W=U\cap V$. Since both $U,V$ are open by assumption, we have:
- there is $P\in \gamma$ such that $x\in P \subset U$;
- there is $Q\in \gamma$ such that $x\in Q \subset V$.
In particular, we have $x\in P\cap Q$, and we can apply (B2) to this situation: there is $B\in \gamma$ with $$B\subset P \cap Q.$$ To continue, $$B\subset P \cap Q \subset U\cap V=W.$$ So, we have shown that there is $B\in \gamma$ such that $$x\in B\subset W.$$ By definition, $W$ is open. $\blacksquare$
The construction is illustrated below:
The illustration is inserted after the proof to emphasize that the latter can't rely on -- or even refer to -- pictures.
What about the union? Let's try to recycle the proof for intersection. After all, we will have to use the definition of openness three times again.
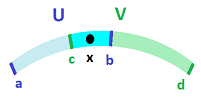
Theorem. The union of two open sets is open.
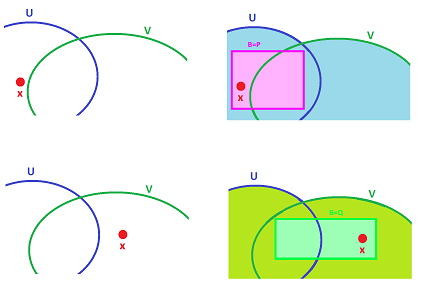
Proof. We copy the proof from above and replace each $\cap$ with $\cup$. This is what we get:
“Suppose $U,V$ are open with respect to $\gamma$ and let $W:=U \cup V$. Suppose $x\in W$ is given.
Given $x\in W=U\cup V$. Since both $U,V$ are open by assumption, we have:
- there is $P\in \gamma$ such that $x\in P \subset U$;
- there is $Q\in \gamma$ such that $x\in Q \subset V$.
$\big[$ In particular, we have $x\in P\cup Q$ and we can apply (B2) to this situation: there is $B\in \gamma$ with $$B\subset P \cup Q.$$ To continue, $\big]$ $$B\subset P \cup Q \subset U\cup V=W.$$ So, we have shown that there is $B\in \gamma$ such that $$x\in B\subset W.$$ By definition, $W$ is open.”
Turns out, the part in brackets is unnecessary. Instead we just choose either $B=P$ or $B=Q$ depending on whether $P$ or $Q$ contains $x$.
$\blacksquare$
Why the proof is easy is illustrated below:
Theorem. The union of any collection of open sets is open.
Exercise. Prove this theorem (a) by following the proof of the last theorem, and (b) as a corollary.
Of course, a subset $A\subset X$ will be called closed if its complement $X \setminus A$ in $X$ is open.
From bases to topologies
Let's summarize the results of the last subsection.
Theorem. Given a basis of neighborhoods $\gamma$, let $\tau$ be the set of all open sets with respect to $\gamma$. Then $\tau$ satisfies the following conditions:
- (T1) $\emptyset, X \in \tau$;
- (T2) if $\alpha \subset \tau$ then $\cup \alpha \in \tau$;
- (T3) if $U,V \in \tau$ then $U \cap V \in \tau$.
Exercise. Prove (T1).
Definition. Given a basis of neighborhoods $\gamma$, the collection $\tau$ of all sets open in $X$ with respect to $\gamma$ is called the topology of $X$ generated by $\gamma$.
The smallest possible basis on set $X$ is $$\gamma_a := \{X \}.$$ The topology it generates is called the anti-discrete topology: $$\tau_a = \{\emptyset, X \}.$$
The largest possible basis is the set of all subsets of $X$ $$\gamma_d := \{A \subset X \} =2^X.$$ The topology it generates is called the discrete topology; it coincides with the basis: $$\tau_a = \{A \subset X \} =2^X.$$ However, this topology is more economically generated by the basis of all singletons: $$\gamma_s = \{\{x\}:\ x\in X \}.$$
Theorem. All neighborhoods are open, i.e., $$\gamma \subset \tau.$$
Proof. Indeed,
- (T1) $\Rightarrow$ (B1);
- (T3) $\Rightarrow$ (B2).
$\blacksquare$
A basis can now be easily enlarged with open sets.
Proposition. If $U$ is open with respect to basis $\gamma$, then $\gamma \cup \{U\}$ is also a basis.
Exercise. Prove the proposition.
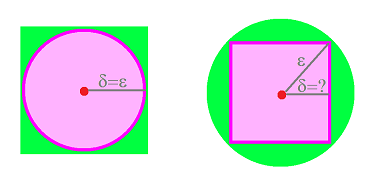
We can refine the basis of disks $B(x,\epsilon)$ with that of squares $S(x,\delta)$ and vice versa:
Lemma. For any $x\in {\bf R}^2$,
- for any $\epsilon >0$ there is $\delta>0$ such that $B(x,\delta)\subset S(x,\epsilon)$; and
- for any $\epsilon >0$ there is $\delta>0$ such that $S(x,\delta)\subset B(x,\epsilon)$.
Theorem. The topology $\tau_d$ generated by the disks $\gamma_d$ is the same as the topology generated by the squares.
Exercise. Prove the lemma and the theorem.
Another basis in ${\bf R}^2$ is $\gamma_q$, the quadrants: $$Q(r,s)= \{(x,y) \in {\bf R}^2 :\ x > r, y > s \}.$$
Exercise. Prove that it is.
Disks refine quadrants but not vice versa! This suggests the following.
Theorem. The topology $\tau_d$ generated by the disks $\gamma_d$ is NOT the same as the topology $\tau_q$ generated by the quadrants $\gamma_q$.
Exercise. Prove the theorem. Hint: you just need a single example of an open set.
When two bases generate the same topology they are called equivalent.
For a given set $X$, the "sizes" of topologies on $X$ vary -- between the anti-discrete and the discrete. This is the hierarchy for $X={\bf R}^2$: $$\tau_a \subset \tau_q \subset \tau_d \subset \tau_d.$$
Exercise. Determine which of the following collections are bases of neighborhoods; find their topologies when they are, and identify the equivalent ones:
- $\{[a, b) \subset {\bf R} :\ a < b\}$,
- $\{(n, n + 2) \subset {\bf R} :\ n \in {\bf Z}\}$,
- $\{[a, b] \subset {\bf R} :\ a < b\}$,
- $\{[a, b] \subset {\bf R} :\ a ≤ b\}$,
- $\{(−x, x) \subset {\bf R} :\ x \in {\bf R}\}$,
- $\{(−\infty, q) \subset {\bf R} :\ q \in {\bf Q}\}$,
- $\{\{a\} \times (b, c) \subset {\bf R}^2 :\ a, b, c \in {\bf R}\}$.
Exercise. Prove that the set of all right half-intervals in ${\bf R}$ is a basis of neighborhoods: $$\gamma = \{[a,b):\ a < b \}.$$
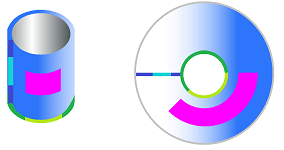
Exercise. Provide formulas for these neighborhoods on the cylinder and the ring and prove that they form a basis:
From topologies to bases
We may choose to enter Topology, as we did, through the door that leads to the bases of neighborhoods and then to the topologies, or we might start with the topologies. We simply turn a theorem into a definition, as follows:
Definition. Given a set $X$, any collection $\tau$ of subsets of $X$ is called a topology on $X$ if it satisfies the following three conditions:
- (T1) $\emptyset, X \in \tau$;
- (T2) if $\alpha \subset \tau$ then $\cup \alpha \in \tau$;
- (T3) if $U,V \in \tau$ then $U \cap V \in \tau$.
The elements of $\tau$ are still called open sets.
The set paired up with a topology, $(X,\tau)$, is called a topological space.
Just as above, the smallest possible topology on $X$ is $$\tau_a := \{ \emptyset, X \}.$$ It is called the anti-discrete topology.
The largest possible is the set of all subsets of $X$ $$\tau_d := \{ A \subset X\}=2^X.$$ It is called the discrete topology.
We restate the above theorem as a relation between bases and topologies.
Theorem. Given a basis $\gamma$, the collection $\tau$ of all sets open with respect to $\gamma$ is a topology.
In this case, we still say that basis $\gamma$ generates topology $\tau$.
The issue of “topological space vs. its basis” is similar to that of “vector space vs. its basis”. Indeed, in either case
- the space is generated by its basis, and
- there are many possible bases for the same space.
The dissimilarity is in the fact that there is no requirement for a basis of neighborhoods to be as small as possible. In fact, $\tau$ is generated by $\tau$.
Exercise. Suppose
- $X$ is a set,
- $\gamma$ is a basis of neighborhoods on $X$,
- $\tau$ is a topology on $X$ (unrelated to $\gamma$),
- $A$ is a subset of $X$.
Define:
- $\gamma ':=\{N\cap A:\ N\in \gamma\}$,
- $\tau ':=\{U\cap A:\ U\in \tau\}$.
Prove:
- (a) $\gamma '$ satisfies condition (B2),
- (b) $\tau '$ satisfies conditions (T2) and (T3).
Theorem. The intersection of any finite collection of open sets is open.
Exercise. Prove the theorem.
Path-connectedness
Since we defined continuity in terms of open sets, the idea of what functions are continuous will entirely depend on the choice of topology for our spaces. Here, we investigate path-connectedness in this environment.
We will need these three things here:
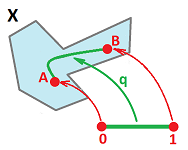
$\bullet$ A topological space $X$ is path-connected, if for any two points $A, B \in X$ there is a continuous function $q : [0,1] \to X$ such that $q(0)=A$, $q(1)=B$;
$\bullet$ function $f:X\to Y$ is continuous if for any $U \in \gamma _Y$ there is $V \in \gamma _X$ such that $f( V ) \subset U$;
$\bullet$ the topology of $[0,1]$ is Euclidean generated by the set of all open intervals $\gamma$.
You are to demonstrate now how misleading the above illustration is.
Exercise. Suppose $X,Y$ are two topological spaces, one of which is (a) discrete or (b) anti-discrete. Determine under what circumstances a function $f:X\to Y$ is continuous. Specifically, answer these questions:
- What topology for the domain or target space would guarantee that $f$ is continuous?
- What function $f$ would be continuous regardless of the topology these spaces?
Exercise. Use the last exercise to discuss path-connectedness of the discrete and anti-discrete topologies.
Exercise. Prove that
- with respect to discrete topology, every singleton is a path-component;
- with respect to anti-discrete topology, the whole set is path-connected.
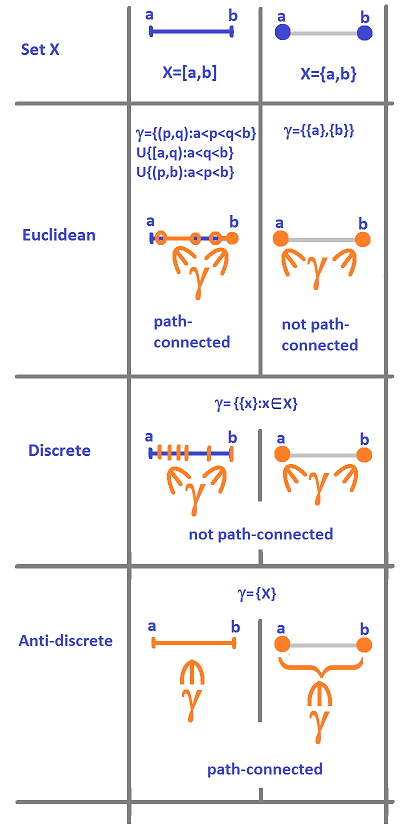
The diagram below illustrates the idea that simple topological concepts, such as path-connectedness, are meaningless until the topology is specified. Two sets, the interval $[0,1]$ and two points $\{0,1\}$, are equipped with various topologies and then path-connectedness is determined for either of them.
It appears that the two topologies at the two extremes of our hierarchy are, indeed, extreme.