This site is being phased out.
Multilinear algebra
Contents
- 1 Multivectors
- 2 Tangent spaces of cell complexes
- 3 Spaces of multivectors
- 4 Multivectors as simplicial chains
- 5 Tangent multivectors vs. chains
- 6 Forms as multilinear functions
- 7 Forms vs. cochains
- 8 Formulas for the wedge product of forms
- 9 Properties of the wedge product of forms
- 10 The tangent bundle
- 11 Differential forms vs. cochains
Multivectors
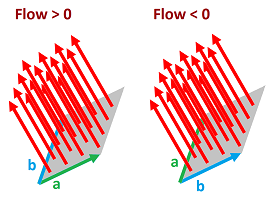
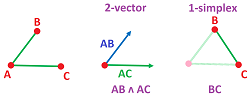
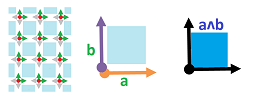
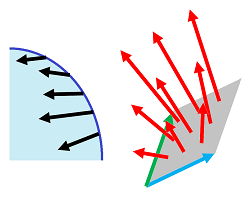
Two vectors determine a parallelogram. Its area is all we need to find the amount of liquid carried through by a given (normal) current. However, to be able to tell whether the flow through this parallelogram is positive or negative, we need to fix its orientation. It can be done by ordering the two vectors.
Given a module $V$ over a ring $R$, we think of multivectors over $V$ as ordered “combinations” of vectors in $V$:
- $1$-vector $v_1 \in V$;
- $2$-vector $v_1 \wedge v_2$ with $v_1,v_2 \in V$;
- $3$-vector $v_1 \wedge v_2 \wedge v_3$ with $v_1,v_2,v_3 \in V$; etc.
Here the wedge symbol $\wedge$ is used just to string the vectors together for now. The nature of these entities will be revealed by their algebraic properties.
To evaluate the flow, we need to consider some geometry: how large are these entities?
- The magnitude of $1$-vector $v_1$ is the length of this vector.
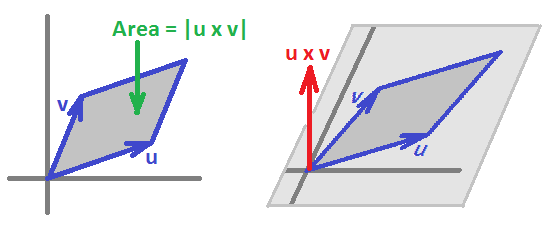
- The magnitude of $2$-vector $v_1 \wedge v_2$ can be interpreted as the area of the parallelogram with sides $v_1,v_2 \in V$.
- The magnitude of $3$-vector $v_1 \wedge v_2 \wedge v_3$ gives the volume of the parallelepiped spanned by those vectors. And so on.
Now, these magnitudes alone cannot be used to evaluate the flow, as we saw above. This is simple algebra: if we have moved by vector $v_1$ and then $-v_1$ then the result is $0$. They cancel!
The idea of cancelling isn't as immediate for areas. In geometry, we are used to think of areas as always positive. Not until calculus we realize that areas are algebraic too: they can be negative, they can cancel etc., and their signs may depend on how the regions are oriented with respect to the coordinate axes.
For example, the area under the graph of the velocity function is the displacement, which can be negative. Or, this area could be the amount of water gained versus the amount lost etc. The same idea is applicable to the volumes, in any dimension.
The idea of how the sign depends on the orientation also applies to the area of a region spanned by two vectors.
Note: Recall that, in dimension $3$, it can be computed as the cross product $v = a \times b$ or $u = b \times a$.
For completeness sake, we also include $0$-vectors; they are simply numbers. Then, for $k = 0, 1, 2$ and $3$, $k$-vectors are often called respectively scalars, vectors, bivectors, and trivectors.
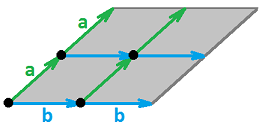
Let's consider how $2$-vectors are formed from $1$-vectors: $$\varphi = a \wedge b.$$ Is this operation linear?
No, as the picture below illustrates:
Indeed, the area of a region like this depends linearly on each of its dimensions, $a$ and $b$, and, as a result, it is quadratic on $(a,b)$.
We call such a dependence multilinear, i.e., it is linear with respect to each variable when all others are fixed.
What about symmetry? As discussed above, multivectors are anti-symmetric: $$a \wedge b = -a \wedge b.$$ It follows, in particular, that $$u \wedge v \wedge w = -v \wedge u \wedge w = -(-v \wedge w \wedge u) = v \wedge w \wedge u.$$ We also have that $$u \wedge u = -u \wedge u$$ and, from linearity, we deduce that $$2u \wedge u = 0,$$ implying the following.
Proposition. $$u \wedge u=0.$$
Tangent spaces of cell complexes
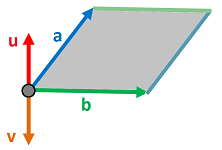
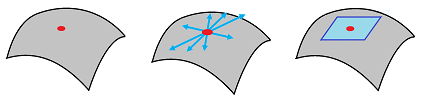
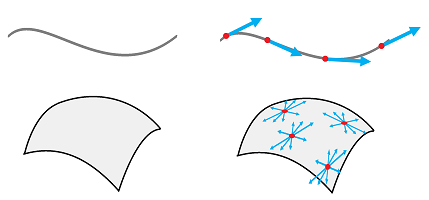
The need to handle directions appears, separately, at every point of the Euclidean space.
The set of all possible directions at point $A\in {\bf R}^n$ form a vector space of the same dimension. It is $V_A$, a copy of ${\bf R}^n$, attached to each point $A$:
What if we replace ${\bf R}$ with an arbitrary ring of coefficients $R$? Then we can choose $V_A$ to be the $R$-module generated by some basis of ${\bf R}^n$, for each $A$.
Next, we apply this idea to cell complexes.
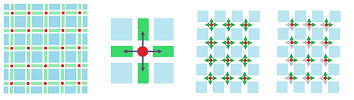
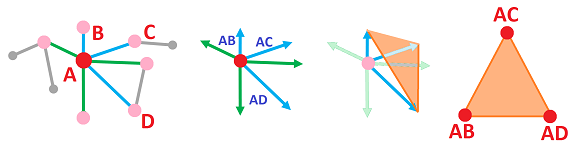
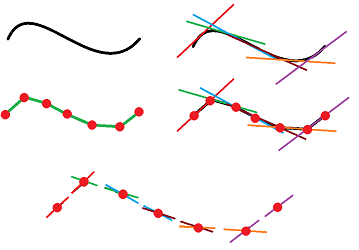
First, what is the set of all possible directions on a graph? We've come to understand the edges starting from a given vertex as independent directions. That's why we have as many vectors as there are edges at each of its points:
Of course, once we start talking about oriented cells, we know it's about chains, over $R$.
Definition. For each vertex $A$ in a cell complex $K$, the (dimension $1$) tangent space at $A$ of $K$ is the set of $1$-chains over $R$ generated by the $1$-dimensional star of the vertex $A$: $$T_A=T_A(K):=< \{AB \in K\} > \subset C_1(K).$$
Proposition. The tangent space $T_A(K)$ is a submodule of $C_1(K)$.
Next, a subcomplex $L\subset K$ inherits its tangents from the ambient complex.
Proposition. For each vertex $A$ in subcomplex $L\subset K$, the tangent space at $A$ of $L$ is the span in $T_A(K)$ of the set of edges in $L$ that originate from $A$: $$T_A(L):=< \{AB \in L \} > \subset T_A(K).$$
Exercise. Prove the proposition.
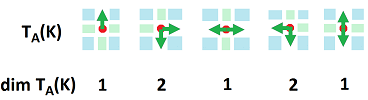
These are the dimensions of the tangent spaces of the discrete curve shown above:
Exercise. (a) Consider the rest of the points. (b) Provide examples, whenever possible, of points on a discrete curve $K$ in ${\bf R}^3$ with: $$\dim T_A(K)=0,1,2,3.$$
Let's next recall that the tangent spaces are defined for any open subset $U$ of ${\bf R}^n$, since any $A\in U$ has a neighborhood isomorphic to ${\bf R}^n$. Furthermore, if an $m$-manifold $X$ is embedded in ${\bf R}^n$, any of its points has a neighborhood $V$ such that $V \cap X \cong {\bf R}^m$. In fact, every point in any $n$-manifold has a neighborhood isomorphic to ${\bf R}^n$. Therefore, we can think of this set as if it determines the set of all possible directions on the $n$-manifold at that point:
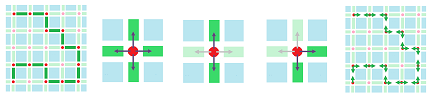
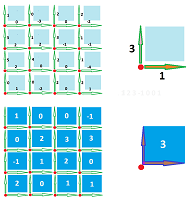
Next, what is the set of all possible directions on the standard cubical complex representation ${\mathbb R}^n$ of the Euclidean space ${\bf R}^n$? There are $2n$ vectors, i.e., oriented edges, attached to each of its points:
Now, the complex ${\mathbb R}^n$ comes with a standard orientation of all edges -- along the coordinate axes. In fact, the edges oriented in the opposite direction -- at the same vertex -- are simply the negatives:
- in ${\mathbb R}^1$:
- $[k,k+1]=-[k,k-1]$;
- in ${\mathbb R}^2$:
- $[k,k+1]\times \{m\} =-[k,k-1]\times \{m\}$,
- $\{k\}\times [m,m+1] =-\{k\}\times [m,m-1]$;
- etc.
Then, when we speak of chains, there is an algebraic redundancy as the opposite directions are represented by two different edges. This is why we omit from the list of possible directions an edge unless it is positively oriented. That's why there need to be only $n$ directions at each vertex to be considered.
Definition. For each vertex $A$ in ${\mathbb R}^n$, the (dimension $1$) tangent space at $A$ is the span in $C_1({\mathbb R}^n)$ of the set of the edges that originate from $A$ and are aligned with the coordinate axes of ${\bf R}^n$: $$T_A({\mathbb R}^n):=< \{AB \in {\mathbb R}^n: A \le B\} > \subset C_1({\mathbb R}^n).$$
Proposition. $$\dim T_A({\mathbb R}^n) = n.$$
This construction is discussed later in more detail.
Spaces of multivectors
Notation. The set of all $k$-vectors in $V$ is denoted by $$\Lambda _k = \Lambda _k (V),\ k=0,1,2,....$$
First, observe: $$\Lambda _0 (V)= R,$$ $$\Lambda _1 (V) = V.$$
Next, $\Lambda _2(V)$ is defined via the wedge product operator: $$\wedge :V \times V \to \Lambda _{2}.$$ We define $\Lambda _{2}$ as a space that consists of these formal sums: $$\sum s_i (v_i \wedge w_i),$$ where $s_i \in R, v_i,w_i \in V$. We make them subject to these algebraic rules: $$\begin{array}{lll} \text{linearity 1: } &(s_1v_1 + s_2v_2) \wedge w = s_1(v_1 \wedge w) + s_2(v_2 \wedge w);\\ \text{linearity 2: } &v \wedge (t_1w_1 + t_2w_2) = t_1(v \wedge w_1) + t_2(v \wedge w_2);\\ \text{cancellation: } &v \wedge v =0;\\ \text{anti-commutativity: } &v \wedge w = - w \wedge v, \end{array}$$ where $$v, v_1,v_2,w, w_1,\ w_2\in V, \ s_1,s_2, t_1,t_2\in R.$$ Note that the linearity can also be seen as distributivity.
Suppose now that $\{v_1,...,v_n \}$ is a basis of $V$. Then any vector in $V$ can be represented as a linear combination of these vectors. In particular, suppose we have $$a=\sum _ia_iv_i,\ b=\sum _ib_iv_i, \ a_i,b_i \in R.$$ Then we can define and compute the wedge product by using the above properties: $$\begin{array}{lll} a \wedge b &:= \left( \sum _ia_iv_i\right) \wedge \left( \sum _jb_jv_j \right)\\ &=\sum _{i,j} a_ib_j (v_i \wedge v_j)\\ &=\sum _{i<j} (a_ib_j -a_jb_i)(v_i \wedge v_j), \end{array}$$
To provide a proper mathematical treatment for this construction, one needs to see the above rules as equivalences of elements in $V \times V$, i.e., strings of vectors: $$\begin{align} (s_1v_1 + s_2v_2, w) \sim s_1(v_1 , w) + s_2(v_2 , w);\\ (v , t_1w_1 + t_2w_2) \sim t_1(v , w_1) + t_2(v , w_2);\\ (v , v ) \sim 0;\\ (v , w ) \sim - (w , v). \end{align}$$ Then we define $$\Lambda _2 (V) := \big( V \times V \big) / _\sim.$$
Exercise. Show it is well-defined.
In that sense, $u \wedge v$ is simply the equivalence class of $u \times v$. Then, the above “rules” become true identities.
The construction is similar for $\Lambda _k(V)$. We start by thinking of $\Lambda _k(V)$ as the space of formal linear combinations (over $R$) of: $$v_1 \wedge v_2 \wedge ... \wedge v_k,$$ where $v_i,w_i \in V$, subject to algebraic rules of linearity, cancellation, and anti-commutativity.
Next, we remove the redundant conditions. First, the linearity is ensured by the structure of $V^k$ itself. Second, the cancellation follows from the anti-symmetry. Therefore, the last is the only condition that is necessary.
Definition. The space of $k$-multivectors $\Lambda _k(V)$ is the quotient of the product space $V^k$: $$\Lambda _k (V) := V^k / _\sim,$$ under the following anti-symmetry equivalence relation:
- $(v_1, v_2 ,..., v_k) \sim -(u_1, u_2 ,..., u_k)$ if the latter is the same as the former with two entries interchanged.
The identification map, $$q:V^k \to \Lambda _k (V),$$ of this equivalence relation will be called the anti-symmetry map.
Exercise. Show that the map is well-defined and linear.
Exercise. Define $\Lambda _k (V)$ via the tensor product.
Notation. Each wedge product stands for a certain equivalence class in $V^k$: $$v_1 \wedge v_2 \wedge ... \wedge v_k:=[(v_1, v_2, ..., v_k) ].$$
Then the equivalences can be rewritten as identities for the wedge product.
Proposition.
- $(su + tw)\wedge v_2 \wedge ...\wedge v_k = s(u \wedge v_2 \wedge ...\wedge v_k) + t(w \wedge v_2 \wedge... \wedge v_k)$;
- $v_1\wedge v_2 \wedge ...\wedge v_k = 0$ if for some pair of indices $i \ne j$, $v_i=v_j$;
- $v_1\wedge v_2 \wedge ...\wedge v_k = -u_1\wedge u_2 \wedge ...\wedge u_k$ if the latter is the same as the former with two entries interchanged.
The last property states that applying a transposition to a multivector flips its sign. The fact that odd/even permutations are compositions of the odd/even number of transpositions imply the following.
Theorem. $$v_1\wedge v_2 \wedge ...\wedge v_k = (-1)^{\pi (s)} v_{s(1)}\wedge v_{s(2)} \wedge ...\wedge v_{s(k)},$$ where $s\in \mathcal{S}_k$ is a permutation and $\pi (s)$ is its parity.
Theorem. If $\dim V =n$, then $$\dim \Lambda _k= \binom {n}{k}.$$
Exercise. Prove the theorem.
In particular, $$\dim \Lambda _n = 1,$$ so $$\Lambda _n = R.$$ We can also assume that $$\Lambda _k = 0,\ \forall k>n.$$
Of course, the most direct way to define this space is as a quotient module. It is the quotient of $V^k$ over the submodule that consists of the strings of vectors that are equivalent to $0$: $$P_k :=\{ v\in V^k: v_i=v_j \text{ for some } i\ne j \}.$$
Proposition. The space of $k$-multivectors is the quotient module: $$\Lambda _k (V) = V^k / P_k.$$
Exercise. Prove the proposition.
Exercise. Finish the sentence “$P_k$ consists of all vectors of the form $v + u, \ u,v\in V^k$, such that...”.
To sum up, the wedge product is an operator: $$\wedge :\Lambda _k \times \Lambda _m \to \Lambda _{k+m}.$$ Together these spaces form a graded module, $$\Lambda := \bigoplus _k \Lambda _k.$$ Then the wedge product is a binary operation within $\Lambda$, $$\wedge :\Lambda \times \Lambda \to \Lambda .$$ This is why it is called the “algebra of multivectors”' or the “exterior algebra”.
Multivectors as simplicial chains
Suppose $\dim V=n$. What is the relation between $\Lambda_0(V), \Lambda_1(V),..., \Lambda_n(V)$?
The following is worth repeating: $$\Lambda_0 (V)=R,\ \Lambda_1 (V)=V.$$
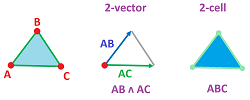
First, bivectors are ordered pairs of edges with the same origin. Then the pair of vectors $AB$ and $AC$ generates the $1$-simplex $BC$:
Furthermore, $2$-vectors are ordered triples and $AB\wedge AC \wedge AD$ generates the $2$-simplex with vertices named $AB,AC,AD$. And so on.
Suppose that the basis of $V$ is ordered. Then, any wedge product of any $k$ vectors of the basis corresponds to an abstract oriented $(k-1)$-simplex: $$v_1\wedge ... \wedge v_k \mapsto v_1v_2...v_k .$$
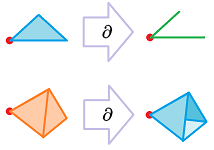
Now, the wedge product of all $n$ elements of the basis is identified with the oriented $n$-simplex $\sigma ^n$. Furthermore, other wedge products of these vectors are the faces of this simplex according to the above correspondence. Consequently, the set of all multivectors is thought of as the chain complex of the simplex: $$\Lambda (V)=C(\sigma ^n).$$ The complex comes with the boundary operator; thus, we have $$\partial: \Lambda_k (V) \to\Lambda_{k-1} (V).$$
Definition. The boundary of a $k$-vector is a $(k-1)$-vector defined by: $$\partial (v_0\wedge ... \wedge v_i \wedge ... \wedge v_k) := \sum_i (-1)^i v_0 \wedge ... \wedge [v_i]\wedge ...\wedge v_k .$$
The boundary operator of a multivectors satisfies the desired double boundary property: $$\partial\partial=0.$$ Thus, we have a chain complex: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{ccccccccccccc} ... & \ra{\partial_{k+2}} & \Lambda_{k+1} & \ra{\partial_{k+1}} & \Lambda_{k} & \ra{\partial_{k}} & \Lambda_{k-1} & \ra{\partial_{k-1}} & ... & \ra{\partial_{1}} & \Lambda_{0} & \ra{\partial_{0}} & 0. \end{array} $$
Theorem. Any linear operator $$f:V\to W$$ generates a chain map $$f_*:\Lambda(V) \to \Lambda (W).$$
Exercise. Prove the theorem.
Next, with the tangent spaces defined, we are now able to form multivectors from $1$-chains in any complex $K$, as long as the edges involved have the same origin.
As an example, the $3$-vectors over $T_A$ are ordered triples of edges with origin at $A$. Then $AB\wedge AC \wedge AD$ generates the $2$-simplex with vertices $AB,AC,AD$ (which can be called $BCD$ as well):
Suppose there are $n$ edges at vertex $A$, i.e., $n$ is the degree of the vertex in this graph. Then $$\dim T_A = n.$$ Suppose that the edges in $T_A$ are ordered (which happens when we choose an ordered basis for $C_1(K)$). Then, the bijection given above maps any wedge product of $k$ edges to an abstract oriented $(k-1)$-simplex: $$AA_1\wedge ... \wedge AA_k \mapsto A_1A_2...A_k .$$ Of course, it doesn't have to belong to $K$.
As discussed above, we have a chain complex $$\Lambda (T_A)=C(\sigma ^n),$$ with the boundary operator $$\partial: \Lambda_k (T_A) \to\Lambda_{k-1} (T_A)$$ given by: $$\partial (AA_1\wedge ... \wedge AA_i \wedge ... \wedge AA_k) := \sum_i (-1)^i AA_1 \wedge ... \wedge [AA_i]\wedge ...\wedge AA_k .$$
Tangent multivectors vs. chains
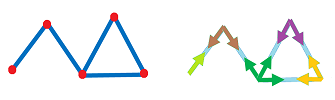
So far, only the edges of the complex have been used. We associated to each vertex $A$ in $K$ an abstract $n$-simplex $\sigma_A$, where $n$ is the degree of the vertex $A$. Is there a counterpart of $\sigma_A$ among the rest of the cells in $K$?
The answer to the last question is “No” if $K$ is a cubical complex and “Maybe” if it is a simplicial complex.
Let's consider simplicial complexes first.
The analysis repeats that in the last subsection. First, bivectors are ordered pairs of edges with the same origin and then the pair of edges $AB$ and $AC$ generates the abstract $2$-simplex $\sigma _A=ABC$:
This simplex may belong to $K$.
The idea applies to all $k$-vectors in $T_A$: any $v\in \Lambda_k (T_A)$ may generate a $k$-simplex in $K$, if such a simplex is present in $K$. On the other hand, every ordering of the $k$ vertices (other than $A$ itself) of a $k$-simplex corresponds to a list of $k$ vectors originating from $A$: $$h:AA_1A_2...A_k \mapsto AA_1\wedge ... \wedge AA_k.$$ The former is an oriented $k$-simplex and the latter a $k$-vector. Thus, every $k$-cell adjacent to $A$ corresponds to some $k$-face of $\sigma_A$, but not vice versa.
Furthermore, this is what we know about permutations in the wedge product of vectors (from this section) and of vertices of a simplex (from subsection 3.5.4). The effect is the same: permuting the vertices of a simplex, or the vectors of a multivector, preserves the simplex/multivector when the permutation is even and flips its sign then it's odd. Therefore, the map given above is well-defined as map of chains: $$h_k:C_k({\rm St}_A) \to \Lambda_k (T_A), \ k=0,1,2....$$
What about the chain complex structure? In the last subsection we provided it for $\Lambda (T_A)$. Meanwhile, $C({\rm St}_A)$ inherits it from $K$. Indeed, if $\partial$ is the boundary operator of a cell complex $K$ then $$\partial :C_k({\rm St}_A) \to C_{k-1}(K)$$ is well-defined as the restriction.
Exercise. Show that $$\partial :C_k({\rm St}_A) \to C_{k-1}({\rm St}_A)$$ is well-defined.
Exercise. Prove that $h$ commutes with the boundary operator.
The theorem below follows.
Theorem. In a tangent space of a simplicial complex $K$, every (non-zero) chain is represented by a single (non-zero) multivector: the function $h$ defined by $$h:AA_1A_2...A_k \mapsto AA_1\wedge ... \wedge AA_k$$ generates a one-to-one chain map for each vertex $A$ in $K$: $$h_k:C_k({\rm St}_A) \to \Lambda_k (T_A), \ k=0,1,2....$$
Exercise. (a) Prove that $h$ is one-to-one. (b) Under what circumstances is it an isomorphism?
Things are especially simple for cubical complexes. On our grid, a vector is an oriented edge, a bivector determines an oriented square,... , a $k$-vector determines an oriented $k$-cube.
There is a one-to-one correspondence between the $k$-vectors at vertex $A$ and the oriented $k$-cubes originating at $A$, as both are represented as combinations -- the products or wedge products -- with $k$ (out of $n$) edges. Suppose $A=(m_1,...,m_n)$ is a vertex. Then a $k$-cube originating at $A$ is: $$Q=I_1\times ... \times I_n,$$ where the $i$th component is either
- an edge $I_i=[m_i,m_i+1]$, or
- a vertex $I_i=\{m_i\}$,
in the $i$th coordinate axis of the grid, with exactly $k$ edges present. Then the cube $Q$ generates a $k$-vector $v=h(Q)$ as the wedge product of the corresponding edges of the cube.
Theorem. In a tangent space of vertex $A$ of a cubical complex $K$, every (non-zero) chain is represented by a single (non-zero) multivector: there is a one-to-one chain map for each vertex $A$ in $K$: $$h_k:C_k({\rm St}_A) \to \Lambda_k (T_A), \ k=0,1,2....$$
Exercise. Give a formula for $h$: $$v=h(Q):= [\ \ ] \wedge \ ...\ \wedge [\ \ ],$$ and prove the theorem.
Definition. A cell complex $K$ that has such a one-to-one chain map $h=\{h_k\}$ for each of its vertices $A$ is called regular. The monomorphism will be called the de Rham map of $K$.
Thus, both simplicial and cubical complexes are regular.
For a general cell complex, such a correspondence might not be one-to-one, as the illustration below shows:
Exercise. (a) Suggest a generalization of $h$ for the case of general cell complexes. (b) Find examples in all dimensions to show that $h$ doesn't have to be one-to-one. (c) Find necessary conditions when it is.
Things are even simpler for $K={\mathbb R}^n$. First, there is a multivector for each cube, just as above. Furthermore, unlike the general cubical case, there is only one such a multivector because of the way we defined its tangent spaces.
Theorem. In a tangent space of vertex $A$ of $K={\mathbb R}^n$, the chains are the multivectors. Indeed, there is an isomorphism: $$h:C_k({\rm St}_A) \to \Lambda_k (T_A).$$
Exercise. Prove the theorem.
Forms as multilinear functions
Given a module $V$, how does one compute the (algebraic) lengths, areas, volumes, etc. of the multivectors in $V$?
For example, in dimension $2$, the algebraic area of the parallelogram spanned by two vectors $a,b$ is: $$Area = \det\begin{bmatrix} v & w\end{bmatrix} = \det\begin{bmatrix} a & c\\b & d \end{bmatrix} = ad - bc .$$
Definition. A function $$\varphi: V^k \to R.$$ is called a multilinear antisymmetric form of degree $k$ over $V$, or simply a $k$-form, if it satisfies the following:
- $\varphi$ is linear with respect to each $V$;
- $\varphi$ is antisymmetric with respect to $V^k$.
Notation. The set of such $k$-forms over $V$ is denoted by $\Lambda ^k(V)$.
Example. In dimension $3$, $k$-forms are these functions: $$\varphi : (R^3)^k \to R,$$ with the following properties with respect to each $R^3$.
- Multilinearity:
- For $\varphi(\cdot,b,c)$ : $\varphi(\alpha u + \rho v,b,c) = \alpha \varphi(u,b,c) + \rho \varphi(v,b,c)$;
- For $\varphi(a,\cdot,c)$ : $\varphi(a,\alpha u + \rho v,c) = \alpha \varphi(a,u,c) + \rho \varphi(a,v,c)$
- For $\varphi(a,b,\cdot)$ : $\varphi(a,b,\alpha u + \rho v) = \alpha \varphi(a,b,u) + \rho \varphi(u,b,v)$
- Antisymmetry:
- $\varphi(x,y,c) = -\varphi(y,x,c)$
- $\varphi(a,y,z) = -\varphi(a,z,y)$
- $\varphi(x,b,z) = -\varphi(z,b,x)$
$\square$
The algebra that we have considered gives $\Lambda ^k(V)$ an algebraic structure.
Proposition. $\Lambda ^k(V)$ is a module under the usual operations of addition and scalar multiplication of functions: $$+ : \Lambda^k \times \Lambda^k \to \Lambda^k,$$ $$\cdot : R \times \Lambda^k \to \Lambda^k.$$
Note that $V$ may have no geometric structure. The inner product and, therefore, geometric lengths (distances) and angles aren't being considered, at this time. In this sense, the discussion is purely algebraic.
Proposition. Multilinearity and the antisymmetry are preserved under the operations of $\Lambda^k$.
Exercise. Prove this proposition.
Recall also that $$\Lambda_k(V):=V^k/P_k,$$ where $P_k$ consists of all $v\in V^k$ such that $v_i=v_j$ for some $i\ne j$. Then transposition $s=(ij)$, i.e., interchanging the $i$th and the $j$th coordinates, makes this $v$ equivalent to $0$: $$s(v)\sim 0.$$ Also, for any $\varphi\in \Lambda^k(V)$, we have: $$\varphi(v)=\varphi(s(v))=-\varphi(v) \ \Rightarrow \ \varphi(v)=0.$$ We have proven the following.
Proposition. For any $\varphi\in \Lambda^k(V)$, we have $$[\varphi](P_k)=0.$$
The proposition allows us to define forms as linear functions on multivectors: $$[\varphi]: \Lambda_k(V) \to R.$$ Indeed, $[\varphi]([v])$ is now well defined. It is seen in this commutative diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccc} V^k & \ra{\varphi} & R \\ \da{q} & \nearrow _{[\varphi]} & \\ \Lambda_k (V),& \end{array} $$ where $q$ is the antisymmetry map. In fact, $P_k$ is the kernel of $q$. We have proven the following.
Theorem. The module $\Lambda^k$ of all $k$-forms is isomorphic to the dual space of the space of multivectors: $$[q]^*:\Lambda^k \cong (\Lambda_k)^*.$$
In other words,
Forms vs. cochains
The space of multivectors on a cell complex $K$ at vertex $A$ is denoted by $\Lambda_k (T_A(K))$. For simplicial and cubical complexes we have expressed this space in terms of their spaces of chains. Next, we consider the space of multilinear functions, forms, on this module $\Lambda_k (T_A(K))$ and, whenever possible, express it in terms of its spaces of cochains. The theorem in the last subsection has important consequences.
The following is obvious.
Proposition. For any cell complex $K$, we have: $$\Lambda^1 (T_A)=(T_A)^*=(C_1({\rm St}_A))^*=C^1({\rm St}_A).$$
We know that, for regular complexes (such as both simplicial and cubical complexes), every $k$-chain is represented by a $k$-vector. Suppose $\varphi$ is a $k$-form on $T_A$, where $A$ is a vertex. Since there is $k$-vector $v$ corresponding to every $k$-cell $q\in {\rm St}_A$, we can define it as a function, $$\psi (v):=\varphi (q).$$ This is a function linear on chains of cells. Thus, we have found a representation of the $k$-vector as a $k$-cochain.
Another way to arrive to this conclusion is to consider the de Rham map: $$h:C_k({\rm St}_A) \to \Lambda_k (T_A),$$ and then build its dual: $$h^*:\left( C_k({\rm St}_A) \right)^* \leftarrow \left(\Lambda_k (T_A) \right)^*.$$ The dual will also be called the de Rham map of $K$. From subsection 6.3.3, we conclude that $h^*$ is onto. Therefore, we have the following crucial result.
Theorem. In a tangent space of a regular cell complex, every $k$-form is represented by a unique $k$-cochain and every $k$-cochain is represented by a (possibly non-unique) $k$-form: there is an epimorphism $$h^*:\Lambda^k (T_A) \to C^k({\rm St}_A).$$
Proof. We use the two identities: $$(C_k)^*=C^k$$ from section 6.3 and $$(\Lambda_k)^*=\Lambda^k$$ from the last subsection. $\blacksquare$
“Missing” cells is what causes the mismatch.
Example. Let $K:=\{A,B,C,AB,BC,CA,ABC\}$ be the simplicial complex of the “filled triangle”. Of course, edges are vectors of our tangent space, so that $H(AB)=AB,...$ and, therefore, $h^*(AB^*)=AB^*,...$. Moreover, since the $2$-chain $ABC$ corresponds to the $2$-vector $AB\wedge AC$, it follows that the cochain $ABC^*$ corresponds to the $2$-form $(AB\wedge AC)^*$.
Next, let $K:=\{A,B,C,AB,BC,CA\}$ be the simplicial complex of the “hollow triangle”. The correspondence between edges and vectors still holds, but, in the absence of $ABC$, what is the match for $AB\wedge AC$? It's $0$. Let's compute: $$\begin{array}{lll} <h^*(AB\wedge AC)^*,AB\wedge AC>&=<(AB\wedge AC)^*,h(AB\wedge AC)>\\ &=<(AB\wedge AC)^*,0>\\ &=0. \end{array}$$ $\square$
Since some of the forms are mapped to zero under this correspondence, our conclusion is that, in general,
- cochains aren't an adequate substitute for forms.
In ${\mathbb R}^n$, the de Rham map $h$ is an isomorphism, which makes things simpler.
Theorem. In a tangent space of ${\mathbb R}^n$, every $k$-form is a $k$-cochain and vice versa.
Exercise. Provide details of the proof.
Formulas for the wedge product of forms
Next, we will specify a basis of $\Lambda^k$ given by explicit formulas.
It all starts when the domain $V=R^n$ is supplied with a coordinate system. By that we mean introducing an ordered basis $\{e_1,...,e_n\}$. The result is that interchanging two elements of the basis amounts to a new basis, which requires a “change of variables” in all computations. This assumption makes the space oriented and explains why $e_x \wedge e_y \ne e_y \wedge e_x$.
At first, we'll stay in lower dimensions, $2$ and $3$, and rely on:
- the standard basis: $\{e_x, e_y, e_z\}$, and
- the variables: $v_x,v_y,v_z$.
What can we way about $1$-forms?
We start by associating to the basis' elements $e_x$ and $e_y$ in $R^2$ a set of basis' elements of $\Lambda$. We define the forms by their values on the basis: $$g_x(e_x)=1,\ g_x(e_y)=0;$$ $$g_y(e_x)=0,\ g_y(e_y)=1.$$ In other words, we have $$g_i(e_j)=\delta _{ij}.$$ This is a familiar example of duality: $$g_x=e_x^*,\ g_y=e_y^*.$$ The analytical representations of these forms are:
- $g_x(v_x,v_y)=v_x,$
- $g_y(v_x,v_y)=v_y.$
Now, what about the rest of $1$-forms? They are to be found as linear combinations of the “basic forms”: $$\varphi^1=Ag_x+Bg_y,\ A,B\in R.$$ We just evaluate this formula with the usual meanings of the algebraic operations: $$\varphi^1(v_x,v_y)=A \cdot v_x+B \cdot v_y.$$
Exercise. For $1$-forms, verify the linearity with respect to $(v_x,v_y)$ and then show that all $1$-forms have been found.
Proposition. $\{g_x,g_y\}$ is a basis of $\Lambda^1(R^2)$: $$\Lambda^1=<\{g_x,g_y\}>.$$
Exercise. Prove this proposition.
So far, this has been a familiar discussion of duality. For $2$-vectors, we will need more, the wedge product of forms: $$\psi^2=Ag_x \wedge g_y,$$ or, in $3$-space, $$\psi^2=Ag_x\wedge g_y+Bg_y\wedge g_z+Cg_z\wedge g_x.$$ The idea is that all forms are linear combinations of the wedge products of the basic forms: $$g_x\wedge g_y,\ g_y\wedge g_z,\ g_z\wedge g_x.$$ These will be constructed from the basic $1$-forms we already understand, $g_x,g_y$. But how? We could just try to multiply them: $$(g_x \wedge g_y)() \stackrel{?}{=} g_x() \cdot g_y().$$ Since we can multiply two functions, such a function makes sense.
Exercise. What kind of algebraic structure is $(\Lambda ^1, +, \cdot)$?
However, this isn't what we want as antisymmetry fails with $g_x \cdot g_y=g_y \cdot g_x$. Moreover, $g_x \cdot g_y$ is a $1$- not a $2$-form! Indeed we have: $$(g_x \cdot g_y)(v_x,v_y) = g_x(v_x,v_y) \cdot g_y(v_x,v_y).$$
After examining this formula, it becomes clear that to produce a $2$-form from two $1$-forms, we shouldn't “recycle” the variables. We will need to define $$(g_x \wedge g_y)(v_x,v_y,v'_x,v'_y)=?$$ as a function of four variables. What should be the formula for the wedge product?
First, it has to be linear on $(v_x,v_y)$ and linear on $(v'_x,v'_y)$. The usual multiplication works: $$g_x(v_x,v_y) \cdot g_y(v'_x,v'_y),$$ but without antisymmetry. The solution is to flip the variables and then combine the results: $$(g_x \wedge g_y)(v_x,v_y,v'_x,v'_y) = g_x(v_x,v_y) \cdot g_y(v'_x,v'_y) - g_x(v'_x,v'_y) \cdot g_y(v_x,v_y).$$ This suggests that we should define the wedge product by: $$(\varphi ^1 \wedge \psi ^1)(v,v'):= \varphi ^1(v) \cdot \psi ^1(v') - \varphi ^1(v') \cdot \psi ^1(v).$$
So, the explicit formula of our new form is: $$(g_x \wedge g_y)(v_x,v_y,v'_x,v'_y) = v_xv'_y - v_yv'_x.$$ Of course, we recognize this as the determinant.
Thus, we have found a way to construct from the two familiar, and explicitly defined, $1$-forms named $g_x$ and $g_y$, a new $2$-form named $g_x \wedge g_y$.
In the general case, we use the fact that those two form a basis of $\Lambda^1(R^2)$ and we also require the wedge product, $$\wedge : \Lambda^1 \times \Lambda^1 \to \Lambda^{2},$$ to be linear on either of the components. Then we compute: $$\begin{array}{lll} \varphi^1\wedge\psi^1&=(Ag_x+Bg_y)\wedge(Cg_x+Dg_y)\\ &=Ag_x\wedge Cg_x+Ag_x\wedge Dg_y+Bg_y\wedge Cg_x+Bg_y\wedge Dg_y, \text{ then by linearity... }\\ &=ACg_x\wedge g_x+ADg_x\wedge g_y+BCg_y\wedge g_x+BDg_y\wedge g_y, \text{ then by antisymmetry...}\\ &=AC0+ADg_x\wedge g_y+BCg_y\wedge g_x+BD0\\ &=(AD-BC)g_x\wedge g_y. \end{array}$$ We notice that this coefficient is equal to a certain determinant: $$AD-BC=\det \left[ \begin{array}{ccc} A & B \\ C & D \end{array} \right]. $$ This number also represents the area of the parallelogram spanned by the vectors $u=(A,B),v=(C,D)$ in the plane:
This idea is also visible in dimension $3$: $$\varphi^1\wedge\psi^1=(Ag_x+Bg_y+Cg_y)\wedge(Dg_x+Eg_y+Fg_z).$$ We just quickly collect the similar terms here while dropping zeros: $$\begin{array}{ll} =(AE-BD)g_x \wedge g_y\\ +(BF-CE)g_y \wedge g_z\\ +(AF-CD)g_x \wedge g_z. \end{array}$$ This looks very similar, not by coincidence, to $$u \times v = (A,B,C) \times (D,E,F) = \det \left[ \begin{array}{ccc} i & j & k \\ A & B & C \\ D & E & F \end{array} \right]. $$
Properties of the wedge product of forms
The idea is to study forms, such as $f$ and $g$, as well “$2$-forms”, such as $f \wedge g$, which is simply $f$ and $g$ paired up, and “$3$-forms” $f \wedge g \wedge h$, etc. The properties that we have seen are required from these forms. For example, the $2$-forms should be bilinear and anti-symmetric.
The $k$-forms capture the oriented $k$-volumes:
- lengths are linear,
- areas are bi-linear,
- volumes are tri-linear, etc.,
just as above.
Warning: These are not the same as the arc-length, surface area, etc., which are independent of orientation and dependent on the inner product.
Back to the wedge product of forms.
We already have an idea that this operator behaves as follows: $$\wedge: \Lambda^k \times \Lambda^m \to \Lambda^{k+m},$$ that is, multiplication of lower degree forms yields higher degree forms.
We already understand the wedge product for the degree $1$ forms in all dimensions. For dimension $3$, the construction for all forms can be easily outlined. First we list the bases of the spaces of forms of each degree:
- $\Lambda ^0(R^3) :\ \{1\}$;
- $\Lambda ^1(R^3) :\ \{g_x,\ g_y,\ g_z\}$;
- $\Lambda ^2(R^3) :\ \{g_x \wedge g_y,\ g_y \wedge g_z,\ g_x \wedge g_z\}$;
- $\Lambda ^3(R^3) :\ \{g_x \wedge g_y \wedge g_z\}$;
- $\Lambda ^k(R^3) =0$ for $k>3$.
Next we define the wedge product as a linear operator $$\wedge \colon \Lambda^k(R^3) \times \Lambda^m(R^3) \to \Lambda^{k+m}(R^3)$$ in the usual way.
For each pair of the basis' elements of the domain spaces we express their wedge product in terms of the basis of the target space. For example, we have: $$\begin{array}{lll} \wedge : \Lambda^0 \times \Lambda^1 \to \Lambda^{1}\\ \quad\wedge(1,g_x)=1 \wedge g_x =g_x,\ \wedge(1,g_y)=1 \wedge g_y =g_y,\ \wedge(1,g_z)=1 \wedge g_z =g_z;\\ \wedge : \Lambda^1 \times \Lambda^1 \to \Lambda^{2}\\ \quad\wedge(g_x,g_y)=g_x \wedge g_y,\ \wedge(g_y,g_z)=g_y \wedge g_z ,\ \wedge(g_x,g_z)=g_x \wedge g_z;\\ \quad\wedge(g_y,g_x)=g_y \wedge g_x =-g_x \wedge g_y,\ \wedge(g_z,g_y)=g_z \wedge g_y =-g_y \wedge g_z,\ \wedge(g_z,g_x)=g_z \wedge g_x =-g_x \wedge g_z;\\ \quad\wedge(g_x,g_x)=g_x \wedge g_x =0,\ \wedge(g_y,g_y)=g_y \wedge g_y =0,\ \wedge(g_z,g_z)=g_z \wedge g_z =0;\\ ... \end{array}$$ We conclude that these conditions fully define $\wedge$ as a linear operator.
Clearly, these spaces aren't closed under the wedge product which is what we are used to. To make it a self-map, we use a graded vector space: $$\Lambda^*:=\Lambda^0 \times \Lambda^1 \times \Lambda^2 \times ... ,$$ $$\wedge: \Lambda^* \to \Lambda^* .$$ Observe that this approach also allows adding any two forms not just ones of the same degree.
We will refer to the forms $$g_x,g_y,\ g_x \wedge g_y,\ ...,\ g_{x^{i_1}} \wedge ... \wedge g_{x^{i_k}}$$ as the basic forms.
Theorem. The wedge product is associative.
Example. Prove the theorem.
Is the wedge product commutative?
No, because we know that $g_x \wedge g_y= -g_y \wedge g_x$.
Is the wedge product anti-commutative?
No, once we realize that $f^0 \wedge \varphi = f^0\varphi$ is simply multiplication.
Example. Consider the product $g_x \wedge g_y \wedge g_z$. By antisymmetry we have $$g_x \wedge g_y \wedge g_z = -g_y \wedge g_x \wedge g_z = g_y \wedge g_z \wedge g_x,$$ so it seems that $$g_x \wedge (g_y \wedge g_z) = (g_y \wedge g_z) \wedge g_x,$$ which suggests that multiplication of forms may be commutative. However, consider the product in $R^4$: $$g_x \wedge g_y \wedge g_z \hspace{1pt} g_u = -g_y \wedge g_x \wedge g_z \wedge g_u = g_y \wedge g_z \wedge g_x \wedge g_u = -g_y \wedge g_z \wedge g_u \wedge g_x.$$ So we cannot say in general that multiplication of forms is a commutative operation.
$\square$
So the answer is, it depends on the degrees of the forms.
It is clear now that we can rearrange the order of the terms step by step and every time the only thing that changes is the sign. Then there must be a general rule here: $$\varphi \wedge \psi = (-1)^{?}\psi \wedge \varphi.$$ What is the sign? It depends only on the number of flips we need to do.
All we know so far is that, if $\varphi \in \Lambda^k$ and $\psi \in \Lambda^m$, then $\varphi \wedge \psi$ is an $(m+k)$-form.
Example. Let $\varphi = g_x \wedge g_y$ and $\psi = g_z \wedge g_u$. Then $$\varphi \wedge \psi = g_x \wedge g_y \wedge g_z \wedge g_u = g_z \wedge g_u \wedge g_x \wedge g_y.$$ To understand the sign, we observe that we simply count the number of times we move an item one step left (or right) and use the antisymmetry property: $$(g_x \wedge g_y) \wedge (g_z \wedge g_u)=(-1)^?(g_z \wedge g_u) \wedge (g_x \wedge g_y).$$ $\square$
This suggests that the “commutativity” property for the wedge product might look like this: $$\varphi \wedge \psi = (-1)^4 \psi \wedge \varphi .$$
Indeed, there is a general result.
Theorem (Skew-commutativity of wedge product). Suppose $\varphi \in \Lambda^k$ and $\psi \in \Lambda^m$. Then $$\varphi \wedge \psi = (-1)^{km}\psi \wedge \varphi.$$
Proof. We use linearity to reduce the problem to the one for this kind of form: $$\varphi = g_{x_1} \wedge g_{x_2}... \wedge g_{x_k}, \ \psi = g_{y_1} \wedge g_{y_2} \wedge ... \wedge g_{y_m}.$$ Then our product is $$\varphi \wedge \psi=\left(g_{x_1} \wedge g_{x_2} \wedge ... \wedge g_{x_k}\right) \wedge \left(g_{y_1} \wedge g_{y_2} \wedge ... \wedge g_{y_m}\right).$$ Let's examine it. What if we want to move $g_{y_1}$ to the very beginning? Like this: $$\begin{array}{cccc} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % &\la{k\ jumps}\\ [\ *\ ] & g_{x_1} \wedge g_{x_2} \wedge ... \wedge g_{x_k} \wedge &[ g_{y_1}]& \wedge g_{y_2} \wedge ... \wedge g_{y_m}. \end{array}$$
Such a move requires precisely $k$ jumps -- and as many applications of the antisymmetry property, as follows: $$\begin{array}{ll} &g_{x_1} \wedge g_{x_2} \wedge ... \wedge g_{x_k} \wedge [g_{y_1}]\wedge g_{y_2}\wedge ... \wedge g_{y_m}\\ =(-1)&g_{x_1} \wedge g_{x_2} \wedge ... \wedge [g_{y_1}]\wedge g_{x_k} \wedge g_{y_2}\wedge ... \wedge g_{y_m}&\text{jump }1\\ ...\\ =(-1)^{k-1}&g_{x_1}\wedge [g_{y_1}] \wedge g_{x_2} \wedge ... \wedge g_{x_k} \wedge g_{y_2}\wedge ... \wedge g_{y_m}&\text{jump }k-1\\ =(-1)^k &[g_{y_1}]\wedge g_{x_1} \wedge g_{x_2} \wedge ... \wedge g_{x_k} \wedge g_{y_2}\wedge ... \wedge g_{y_m}&\text{jump }k. \end{array}$$ Therefore, moving $g_{y_1}$ all the way to the left add a factor of $(-1)^k$.
Now, moving $g_{y_2}$ to the right of $g_{y_1}$ also requires precisely $k$ jumps: $$\begin{array}{cccc} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % &\la{k\ jumps}\\ g_{y_1}\wedge[\ *\ ] & g_{x_1} \wedge g_{x_2} \wedge ... \wedge g_{x_k} \wedge &[ g_{y_2}]& \wedge g_{y_3} \wedge ... \wedge g_{y_m}. \end{array}$$ Therefore, our factor becomes $(-1)^k(-1)^k=(-1)^{2k}$. Performing this jumping process for each of the $m$ of $g_{y_i}$ yields the factor of $(-1)^{km}$.
$\blacksquare$
Exercise. State and prove the skew-commutativity property for multivectors.
Corollary. If $\varphi \in \Lambda^k$ and $k$ is odd, then $\varphi \wedge \varphi = 0$.
Exercise. Prove the corollary.
We have proven that either of these two properties implies the other.
Proposition. $$\varphi ^1 \wedge \psi ^1 = -\psi ^1 \wedge \varphi ^1 \Longleftrightarrow \varphi ^1 \wedge \varphi^1 = 0.$$
Exercise. Show that a form of even degree commutes with any other form.
Exercise. Evaluate $\dim \Lambda ^k (0) = ?$
Exercise. Provide explicit formulas of the basic forms in $\Lambda ^2({\bf R}^3)$, i.e., $g_x \wedge g_y,\ g_y \wedge g_z,\ g_z \wedge g_x$. Suggest formulas for the general case of $\Lambda ^k({\bf R}^n)$.
The tangent bundle
What if we have a flow in space $X$ that varies from point to point? Then amount of flow through a bivector will depend on the location of the bivector.
In fact, we'll need a different set of bivectors in each location. The idea it to attach a vector space $V_A$ to every point $A$ in $X$. Then the flow through a bivector at point $A$ in $X$ is a $2$-form $\varphi_A$, different for each $A$: $$\varphi_A: V_A^2 \to R.$$
The setup is as follows. First, we have the space of locations $X$. It may be
- a differentiable $n$-manifold, or
- the set of all vertices $K^{(0)}$ of a cell complex $K$.
Second, to each point $A\in X$, we associate the space of directions determined by the structure of $X$, as we have seen. We call it the tangent space $T_A(X)$ of $X$ at $A$. It may be
- a vector space isomorphic to ${\bf R}^n$ for a differentiable $n$-manifold, or
- a module over $R$ in general.
Definition. A differential form of degree $k$ over $X$ is a $k$-form parametrized by location, i.e., it is a collection of functions, $$\varphi=\{\varphi_A:\ A\in X\};$$ such that each of them, $$\varphi_A: \{A\} \times T_A^k \to R,$$ is a $k$-form on $T_A$, i.e.,
- $\varphi_A$ is linear with respect to each component $T_A$, and
- $\varphi_A$ is antisymmetric with respect to $T_A^k$.
Note: “differential” refers to the possibility of differentiation of the function, with respect to the location parameter.
We can switch from multilinearity on vectors to linearity on multivectors. The switch is seen in this commutative diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccc} \{A\} \times T_A^k & \ra{\varphi_A} & R \\ \da{\{A\} \times q} & \nearrow _{[\varphi_A]} & \\ \{A\} \times\Lambda_k (T_A),& \end{array} $$ where $q$ is the antisymmetry map.
Proposition. Forms on $X$ are combinations of linear functions: $$[\varphi_A]: \{A\} \times \Lambda_k(T_A) \to R,\ A\in X,$$ and vice versa.
In other words, $$[\varphi_A]\in \Lambda^k(T_A).$$
Definition. The $k$-tangent bundle of $X$ is the disjoint union of the $k$-tangent spaces of all locations: $$T_kX:=\bigsqcup _{A\in X} \left( \{A\} \times T_A^k \right).$$
Then a differential $k$-form is seen as a function on $T_kX$.
Definition. The space of $k$-forms on $X$ $$T^k X:=\{ \varphi=\{[\varphi_A]:\ A\in X\}: [\varphi_A] \in \Lambda^k(T_A)\}$$ is called the $k$-cotangent bundle of $X$.
Notation. For a cell complex $K$, we will substitute $T_k(K)$ for $T_k(K^{(0)})$ and we will use $TK$ for $T_1K$.
The location space $X$ may be an $n$-manifold; then $T_AX$ is chosen to be the span, over $R$, of a basis of ${\bf R}^n$. When $R={\bf R}$, we have $T_AX\cong {\bf R}^n$. Then the tangent bundle, if equipped with a certain topology, is a $2n$-manifold.
What about the discrete case?
Suppose we have a cell complex $K$. The directions at vertex $A\in K$ are given by the edges adjacent to $A$. Moreover, we can think of $1$-chains as directions as long as each of their edges starts at $A$. As defined previously, they are subject to algebraic operations on chains and, therefore, form a module, $V_A=T_A(K)$.
Definition. The wedge product of differential forms is defined one location at a time: $$\left(\varphi\wedge\psi\right)_A:=\varphi_A\wedge\psi_A,\ A\in X.$$
Exercise. Prove that the wedge product is well-defined.
Starting with dimension $1$, we have a function $\varphi$ that associates to each location, i.e., a vertex $A$ in $K$, and to each direction at that location, i.e., edge $x=AB$ adjacent to $A$, with $B\ne A$, a number: $$\varphi:(A,AB) \mapsto r\in R.$$ In dimension $2$, a form is evaluated at the location $A\in K^{(0)}$ and each pair of directions at each location, i.e., edges $x=AB,y=AC$ adjacent to $A$, with $B,C\ne A$: $$\varphi:(A,AB,AC) \mapsto r\in R.$$ This is simply a table: $$\begin{array}{c|ccccccccc} A & AB & AC & AD &...\\ \hline AB & \varphi(AB,AB) & \varphi(AB,AC) & \varphi(AB,AD) &...\\ AC & \varphi(AC,AB) & \varphi(AC,AC) & \varphi(AC,AD) &...\\ AD & \varphi(AD,AB) & \varphi(AD,AC) & \varphi(AD,AD) &...\\ ...& ... & ... & ... &... \end{array} $$ Since the maps are antisymmetric, then so are these tables. In particular, the diagonal elements are equal to zero.
Exercise. What form does this table take in higher dimensions?
Next, in order to stitch these “local” forms together into a differential form, we introduced the tangent bundle as the space of all possible locations and directions. Now, a $k$-form on a complex $K$ is a function: $$\varphi: T_kK \to R,$$ which is a $k$-form when restricted to any tangent space.
What is the exterior derivative of a differential $k$-form? It is supposed to show the local (i.e., within the tangent space) change of the value of the form as we move from one $k$-vector to another. We limit ourselves to regular complexes.
First, $0$-forms are $0$-cochains. Therefore, the exterior derivative of a $0$-form is a $1$-form given by the same formula: $$(d f^0) (AB):=f (B)-f (A).$$ The exterior derivative of a $1$-forms is a $2$-form but we don't look at $2$-cells anymore. We define it on the wedge products of any pair of adjacent edges: $$(d \varphi^1) (AB\wedge AC):=\varphi (AB)-\varphi (AC).$$
Exercise. Define $d\psi^2$.
Differential forms vs. cochains
We now return to the issue of forms represented by cochains. We already know that for a regular cell complex $K$, there is the de Rham epimorphism for every vertex $A$: $$h_A^*:\Lambda^k (T_A) \to C^k({\rm St}_A).$$ Stitching these together we build the global de Rham map, as follows.
Theorem. In a regular cell complex, every differential $k$-form is represented by a unique $k$-cochain and every $k$-cochain is represented by a (possibly non-unique) $k$-form: there is a surjection $$h^*:\Lambda^k (TK) \to C^k(K),$$ linear on every tangent space.
Thus, we can't substitute cochains for forms.
However, in some applications, such as diffusion, the preservation of matter is satisfied: the amount of material that leaves location $A$ for location $B$ should be the same as the amount arriving to $B$ from $A$.
Definition. We say that a $1$-form $\varphi$ on a cell complex is balanced if: $$\varphi(A,AB)= -\varphi(B,BA).$$
It follows that such every $1$-form $\varphi$ is well-defined as a linear map on $C_1(K)$. It is a $1$-cochain!
Theorem. The balanced differential $1$-forms are the $1$-cochains: $$T^1 K=C^1(K).$$
Exercise. Provide details of the proof of the theorem.
Exercise. Show that, in general, $T^1 K\ne C^1(K)$.
Exercise. State and prove a $k$-degree analogue of the last theorem. Hint: limit yourself to regular complexes.
The definition and the theorem reveal possibility of a certain redundancy in forms and, therefore, in the construction of the tangent bundle. This redundancy was removed from tangent bundle of ${\mathbb R}^n$ thanks to the inherited algebra of the Euclidean space. Here, we follow this idea and postulate that the direction from $A$ to $B$ is the opposite of the direction from $B$ to $A$.
Definition. The equivalence relation of balance on the tangent bundle of a cell complex is given by: $$(A,AB)\sim -(B,BA).$$
This equivalence reduces the size of the tangent bundle via the quotient construction. Then, one can see the similarity between this space and the tangent bundle for a $1$-manifold:
It looks as if the disconnected parts of $T(K)$, the tangent spaces, are finally glued together.
Theorem. The equivalence relation of balance preserves the operations on each tangent space and, therefore, defines the module $T(K)/_{\sim}$. Moreover, $$TK/_{\sim}=C_1(K).$$ Furthermore, the restrictions of the identification map to the tangent spaces are monomorphisms: $$T_A(K)\to C_1(K).$$
Exercise. Prove the theorem as well as its $k$-degree analogue.
Proposition. The balanced $1$-forms preserve the equivalence relation of balance and, therefore, are well defined as linear maps $\varphi : C_1(K) \to R$.
Without this equivalence relation, the tangent bundle lacks the module structure of $C_1(K)$. However, the other part of the structure of the chain complex $\{C(K)\}$ remains.
Definition. The boundary operator of the tangent bundle of a cell complex $K$ is the function $$\partial_T : TK\to C_0(K),$$ given by $$\partial_T (AB) := B-A,$$ for each $AB\in K$.
Proposition. The boundary operator of the tangent bundle $TK$ is linear on each of the tangent spaces $T_A(K), A\in K$.
Exercise. (a) Prove the proposition. (b) Prove that $\partial_T =\partial p$, where $p:TK\to C_1(K)$ is the identification map of the equivalence relation above.
For ${\mathbb R}^n$, we simply state that the cubical forms are the cubical cochains: $$T^k {\mathbb R}^n/_{\sim}=C^k({\mathbb R}^n).$$ It follows that treating forms as cubical cochains in the last section as a way to introduce discrete calculus is valid, in this limited setting. The construction is further discussed in the next section.
Notation. To denote the set of differential forms, over an arbitrary ring $R$, we will use
- $\Omega^k(M)$ for a differential manifold $M$, and refer to them as continuous forms,
- $T^kK$ for a general cell complex $K$, and refer to them as discrete forms, and
- $C^k(K)$ for a cell complex $K$, and use it for those forms that are simply cochains.
Exercise. Show that all three are $R$-modules.