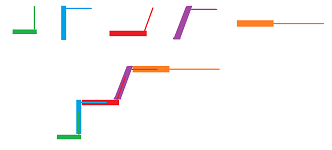Metric tensor in dimensions 1 and 2

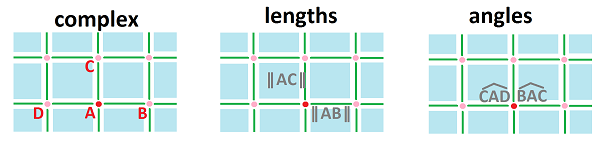
Recall that we need a metric tensor on a cubical complex to provide us with the information necessary for measuring, for each vertex $A$: $$ % \begin{array}{cccccccccc} A & AB & AC & AD &...\\ AB & \lVert AB \rVert & \widehat{BAC} & \widehat{BAD} &...\\ AC & \widehat{BAC} & \lVert AC \rVert & \widehat{CAD} &...\\ AD & \widehat{BAD} & \widehat{CAD} & \lVert AD \rVert &...\\ ...& ... & ... & ... &... \end{array} $$

Dimension 1

Let's consider an example of how we use a metric tensor to establish geometry on a cubical complex.

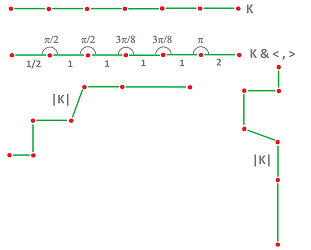
Below you can see the following:

• a cubical complex $K$, a topological construction: cells and their boundaries also made of cells;
• complex $K$ combined with a choice of metric tensor $< \cdot,\cdot >$, a geometric construction: lengths and angles;
• a realization $|K|$ of this combination in ${\bf R}^2$;
• another realization.

As you can see, there are many possible realizations of the same geometric complex. But the lengths are of course the same and the the absolute values of the angles between two consecutive edges are preserved as well. In other words, they are isometric.

There is even more room of variability if we consider realizations in ${\bf R}^3$. Indeed, even with fixed angles one can rotate the edges freely.

We can think of these realizations as constructed of pieces each made of a rod and a tube attached to each other, inserted one into the next:

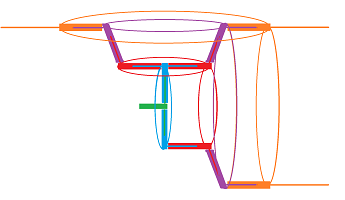
The joints are free to rotate independently while still preserving the lengths and angles:

The ability to rotate these rods underscores the fact that our interest is the intrinsic geometric properties of these objects -- captured by the metric tensor -- just as elsewhere we study intrinsic topological properties -- captured by the cubical complex.

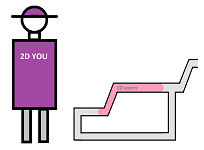
The intrinsic properties are the ones that you can detect while staying inside the object. In the $1$-dimensional case one can think of a worm moving through a tube. The worm can only feel the distance is has passed and the angle its body has to turn:

Meanwhile we can see the whole thing by stepping outside, to the second dimension.

Compare to the 2D vs 3D case:

Dimension 2

A metric tensor is a map on a cubical complex in the plane:

• $AB \mapsto \lVert AB \rVert$;
• $(AB,AC) \mapsto \widehat{BAC}$.

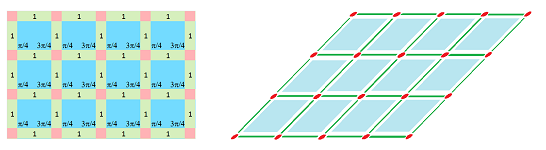
This means that there will be 1 (positive) number per edge and 6 per vertex. To simplify this a bit, below we assume that the opposite angles are equal. This is a type of local symmetry that allows for sufficiently variety of examples in dimension $2$. This way we have only 2 numbers per vertex.

Below we illustrate how we represent

• a topological cubical complex $K$, and
• a geometric complex $(K,<,>)$ on $K$.

Our interest is:

• the realization $|K|$ of the latter.

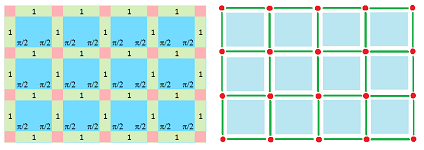
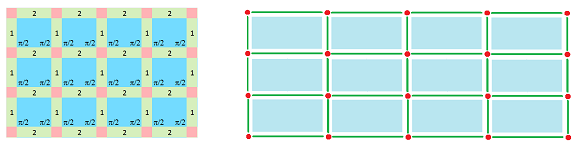
In a few examples below we put the metric data on the left over the complete cubical complex for the whole 2D grid (except for the last one) and then use it as a blueprint to construct a rigid structure on the right.

Square grid:

Rectangle grid:

Rhombus grid:

Exercise. Provide the realization for a metric with lengths: $1,1,1,...$ and angles: $\pi/2,\pi/4,\pi/2,...$.

Cubic grid:

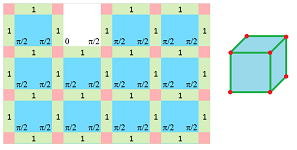
We don't assume anymore that the opposite angles are equal, nor we use the whole grid.

Exercise. Provide the rest of the realization. Construct a cube.