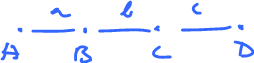Linear operators: part 4

Image and kernel of linear operator

We discuss the subspaces associated with a linear operator.

Suppose $A \colon V \rightarrow U$ is a linear operator, then the kernel of $A$ is

$${\rm ker \hspace{3pt}}A = \{ v \in V \colon A(v)=0 \}$$

the image of $A$ is

$${\rm im \hspace{3pt}}A = \{A(v) \colon v \in V \}.$$

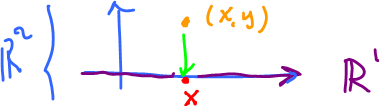
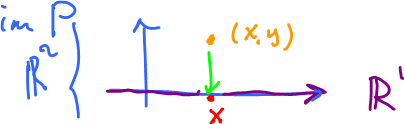
Example: $P \colon {\bf R}^2 \rightarrow {\bf R}^1$ is the projection on the $x$-axis. Its formula is $P(x,y)=x$.

$$\begin{array}{} {\rm ker \hspace{3pt}} P &= \{ v \in V \colon P(v)=0 \} \\ &= \{v = (x,y) \colon P(x,y) = 0 \} \\ &= \{ (x,y) \colon x = 0 \} \end{array}$$

This is the $y$-axis.

Exercise: Consider other projections.

• ${\bf R}^3 \rightarrow {\bf R}^2$, or any plane.
• ${\bf R}^3 \rightarrow {\bf R}^1$, or any line.

Exercise: Let $D \colon {\bf P} \rightarrow {\bf P}$ be the derivative. Then

$$\begin{array}{} {\bf ker \hspace{3pt}} D &= \{ p \in {\bf P} \colon p'=0 \} \\ &= \{ p \colon p {\rm \hspace{3pt} is \hspace{3pt} constant}\}. \end{array}$$

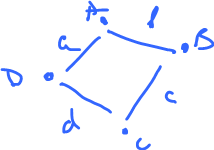
Example: Suppose $G$ is a directed graph.

• vertices $V$, $N$ of them (may be people);
• edges $E$, $n$ of them (may be relations between them).

Define

• $U={\bf R}^N$ with basis being the set of all vectors and
• $W={\bf R}^n$ with basis being the set of all edges.

Define $D \colon W \rightarrow U$, linear operator. On the basis

• $D(e)=B-A$,

where $B$ and $A$ are the end vertices of $e$.

(end point $-$ initial point)

Question: ${\rm ker \hspace{3pt}} D = ?$.

Consider

.

$$\begin{array} D(a+b+c) &= D(a)=D(b)+D(c) \\ &= B-A + C-B + D-C \\ &= D-A \end{array}$$

That's end point $-$ beginning point again!

Now, to get $0$ here, you need $D=A$, i.e., you need a closed loop, "cycle". So,

• $\ker D = $ all cycles of the graph.

Lesson: Linear algebra reveals the topology of the graph.

$D(a+b+c+d)=0$

For more see Algebraic topology: course...

Properties of image and kernel

Theorem: The kernel is always a subspace.

Exercise: ${\rm ker \hspace{3pt}} D^2=?$ $D={\rm differentiation \hspace{3pt}} \colon {\bf P} \rightarrow {\bf P}$. Find the matrix.

Proof: Given operator $A$. We use the Subspace Theorem and need to show:

• 1. $0 \in {\rm ker \hspace{3pt}}A$, yes: $A(0)=0$.
• 2. It's closed under addition, yes: $u,v \in {\rm ker \hspace{3pt}}A$, then $A(u)=A(v)=0$. Consider $u+v$, then $A(u+v)=A(u)+A(v)=0+0=0$, so $u+v \in {\rm ker \hspace{3pt}}A$.
• 3. Closed under scalar multiplication, yes: $u \in {\rm ker \hspace{3pt}}A$, $r \in {\bf R}$, then $A(u)=0$. Consider $ru$, then $A(ru)=rA(u)=r \cdot 0 = 0$, so $ru \in {\rm ker \hspace{3pt}}A$. $\blacksquare$

The image now.

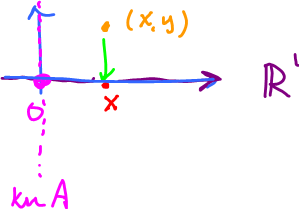
Example: Consider $P \colon {\bf R}^2 \rightarrow {\bf R}^1$, the projection:

.

For each $x$ in $x$-axis, is there a preimage? In other words, can you find $(x,y)$ with $P(x,y)=x$?

Yes!

A more precise diagram:

.

Then $x$ belongs to the image of $P$.

When, for a given $A \colon V \rightarrow U$, do we have ${\rm im \hspace{3pt}}A \neq U$?

• constant function $A \colon V \rightarrow U$, $A(v)=0:$
  • ${\rm im \hspace{3pt}}A = \{0\}$ "small"
  • ${\rm ker \hspace{3pt}}A =V$ "large"
• identity function $id_V \colon V \rightarrow V$, $id_V(x)=x$:
  • ${\rm im \hspace{3pt}}id_V=V$ "large"
  • ${\rm ker \hspace{3pt}}id_V = \{0\}$ "small"

These work in any vector space.

• inclusion $i \colon {\bf R}^1 \rightarrow {\bf R}^2$ (of $x$-axis into the plane) given by $i(x)=(x,0)$ (not as trivial as the zero operator).

Then ${\rm im \hspace{3pt}}i = $ the $x$-axis.

Solve this:

Theorem. $A^{-1}(u)$ is a subspace if and only if $u=0$.

Example: $P^{-1}(x)$, $x \neq 0$, is not a subspace, for the $P$ above.

Example: Suppose $A(v) = 0$ for all $v$, $$\begin{array}{} A^{-1}(x) &\stackrel{ {\rm def} }{=} \{v \colon A(v)=x, x \neq 0 \} \\ &\stackrel{ {\rm sub} }{=}\{v \colon 0=x \} \\ &= \emptyset, \end{array}$$not a subspace.

What do the image and kernel tell us about the linear operator

Recall,

• $A \colon V \rightarrow U$ is onto if ${\rm im \hspace{3pt}}A = U$ (basically the definition);
• $A \colon V \rightarrow U$ is one-to-one if $A^{-1}({\rm point})={\rm point}$ (preimage for every point).

In linear algebra, the last condition can be rewritten and simplified, because we can choose:

$${\rm point}=0,$$

i.e., we have to test only one point. So, the condition turns into $$A^{-1}(0)=\{0\},$$ or $${\rm ker \hspace{3pt}}A=\{0\}.$$

Example: That's why a projection is not one-to-one, but inclusion is.

Theorem: A linear operator $A \colon U \rightarrow V$ is one-to-one if and only if ${\rm ker \hspace{3pt}}A = \{0\}$.

Proof: ($\Rightarrow$) Trivial, done above.

($\Leftarrow$) Assume $A(w)=0$ if and only if $w=0$. (*)

Suppose, $A$ is not one-to-one: there are $u \neq v \in V$ such that $A(u)=A(v)$.

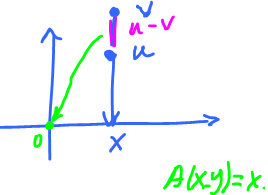
We will have contradiction if we find, based on $u$ and $v$, an element $w \neq 0$ with $A(w)=0$. Then, what is $w$?

The picture suggests: choose $w=u-v$.

Then $$\begin{array}{} A(w) &= A(u-v) \\ &= A(u)-A(v) {\rm (linearity)} \\ &= 0, \end{array}$$

which contradicts the assumption (*). $\blacksquare$

Consider:

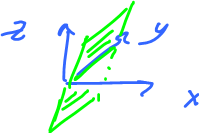plane $z=x$, the graph of $z=f(x,y)=x.$

Now $f$ is not one-to-one. How do we see it in the picture?

"The horizontal plane test", i.e., more than one intersection implies the function is not one-to-one.

How to find kernel

Recall the theorem: The kernel of a linear operator is a subspace.

Exercise: $$\begin{array}{} A: & V \rightarrow & U \\ & \cup & \cup \\ & {\rm ker \hspace{3pt}}A & {\rm im \hspace{3pt}} A \end{array}$$

Practically, we want bases of these subspaces. Need to find their dimensions, at least.

Start with: $$x \in {\rm ker \hspace{3pt}}A {\rm \hspace{3pt} if \hspace{3pt} and \hspace{3pt} only \hspace{3pt} if} Ax=0,$$

which is an "operator equation". It's also a matrix equation, with a basis of $V$ chosen, and, therefore, a system of linear equations (homogeneous!).

Solve it.

The augmented matrix of $AX=0$ is $[A|0]$. Find its reduced row echelon form.

Suppose we already have...

Example: This is the simplest one: $$\left[ \begin{array}{ccc|c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array} \right] $$ Then $$\ker A = \{X=(x_1,x_2,x_3) \colon AX=0 \} = \{X = (0,0,0) \} = \{0\}.$$

Note: we can also think of

$\left[ \begin{array}{ccc|c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array} \right]$ as $\left\{ \begin{array}{} x_1 & & &= 0 \\ & x_2 & &= 0 \\ & & x_3 &=0 \end{array} \right.$

Example: $$\begin{array}{} \left[ \begin{array}{ccc|c} 1 & 0 & 2 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right] &\rightarrow {\rm dim \hspace{3pt} ker \hspace{3pt}} A =1\\ \end{array}$$

Remember: the number of degrees of freedom $=$ the number of free variables.

Here $x_3$ is free: once $x_3$ is given, you get $x_1$ and $x_2$. Why?

$$\ker A = \{X = (x_1,x_2,x_3) \colon x_1+2x_3 = 0, x_2+x_3=0\} $$

These two equations are planes and their intersection is a line.

Looking for a basis, we have to discard all multiples of the basis.

Choose $x_3=1$, then $x_1=-2$ and $x_2=-1$. So $v_1=(-2,-1,1)$.

Now, any $(x_1,x_2,x_3)$ that satisfies the equations is a multiple of $v_1$:

• choose $x_3=c$ then $x_1=-2c$, $x_2=-c_1$, so
• $v=(-2c_1,-c_1,c) = c(-2,-1,1) = cv_1.$

Rule: "the elements of the basis of the kernel corresponds to to free variables".

Example:

$AX=0 \stackrel{ {\rm RRE} }{\rightarrow} \left[ \begin{array}{cccc|c} 1 & 0 & 3 & 0 & 0 \\ 0 & 1 & 1 & 2 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array} \right]$

These columns correspond to respectively $x_1,x_2,x_3$ and $x_4$.

Then $$\ker A = \{(x_1,x_2,x_3,x_4) \colon x_1+3x_3=0 , x_2 + x_3 + 2x_4 = 0 \}.$$ Free variables are $x_3$ and $x_4$.

Choose

• 1. $x_3=1, x_4=0 \rightarrow v_1 = (-3,-1,1,0)$
• 2. $x_3=0, x_4=1 \rightarrow v_2= (0,-2,0,1)$

That's a basis.

Next, the image.

How to find the image

Recall the theorem: The image of a linear operator is a subspace.

This is what we have: $$AX=W$$ where $$\begin{array}{} A: & V \longrightarrow & U \end{array}.$$ Here $X \in V, W \in U$. And their bases are given.

Then $${\rm im \hspace{3pt}}A = \{W \in U \colon {\rm \hspace{3pt} there \hspace{3pt} exists \hspace{3pt}} X \in V {\rm \hspace{3pt} s.t. \hspace{3pt}} AX=W \}$$ Observe that $AX=W$ is a matrix equation.

Now we need to find this subspace or at least its basis.

Example: Suppose we have re-written the matrix equation as (very simple):

$\left[ \begin{array}{ccc|c} 1 & 0 & 0 & v_1 \\ 0 & 1 & 0 & v_2 \\ 0 & 0 & 1 & v_3 \end{array} \right]$

On the left side of the matrix, each column is respectively $x_i$ and the right we label the elements in the last row as $v_i$. It is the latter what we are interested in in!

Find all possible $v_1,v_2,v_3$, for which there are $x_1,x_2,x_3$ that satisfy the equations: $x_1=v_1$, $x_2=v_2$, $x_3=v_3$.

Translated: Given $v_1,v_2,v_3$, $V$, find $x_1,x_2,x_3$, $X$, that satisfy the equations, $AX=W$.

Example: More complex: $$\left[ \begin{array}{ccc|c} 1 & 0 & 2 & v_1 \\ 0 & 1 & 1 & v_2 \\ 0 & 0 & 0 & v_3 \end{array} \right] \longrightarrow \begin{array}{} x_1+2x_3 &= v_1 \\ x_2 + x_3 &= v_2 \\ 0 &= v_3 \end{array}$$

Same issue as before: $(v_1,v_2,1)$ is not in the image. So $v_3=0$, and we concentrate on $v_1,v_2$.

Also: what values of $v_1,v_2,v_3$ are produced when we plug all possible values of $x_1,x_2,x_3$ into the equations?

Rule: "the elements of the basis of the image correspond to dependent variables", i.e., to the leading $1$'s in reduced row echelon form.

Process: Choose

$$x_1=1,x_2=0,x_3=0 \rightarrow v_1=1,v_2=0,v_3=0$$

$$x_1=0, x_2=1, x_3=0 \rightarrow v_1=0, v_2=1, v_3=0$$

Two vectors

• $u_1=(1,0,0)$,
• $u_2=(0,1,0)$

form a basis of the subspace of $U$, which is

$$\{(v_1,v_2,v_3) \colon v_3=0\} = {\rm im \hspace{3pt}} A.$$

This was simple because our system was already in its reduced row echelon form.

Example: Suppose our matrix equation $AX=W$ has turned into this system:

$$\left[ \begin{array}{} 1 & 2 & 3 & v_1 \\ 0 & 1 & 1 & v_2 \\ -1 & 0 & 1 & v_3 \end{array} \right] \longleftrightarrow \begin{array}{} 1 x_1 + 2x_2 + 3x_3 &= v_1 \\ 0x_1 + 1x_2 + 1x_3 &= v_2 \\\ -1x_1 + 0x_2 + 1x_3 &= v_3 \end{array}$$

$$\rightarrow x_1\left[ \begin{array}{} 1 \\ 0 \\ -1 \end{array} \right] + x_2 \left[ \begin{array}{} 2 \\ 1 \\ 0 \end{array} \right] + x_3 \left[ \begin{array}{} 3 \\ 1 \\ 1 \end{array} \right] = \left[ \begin{array}{} v_1 \\ v_2 \\ v_3 \end{array} \right]$$

The results of this algebra is a vector equation.

Again: what values of $v_1,v_2,v_3$ are produced when we plug in all possible values of $x_1,x_2,x_3$ into the equations?

Observe that $x_1,x_2,x_3$ are the coefficients of the linear combination, but of what?)

Consider: $$A \colon V \rightarrow U$$ and $$p_1 = \left[ \begin{array}{} 1 \\ 0 \\ -1 \end{array} \right], p_2 = \left[ \begin{array}{} 2 \\ 1 \\ 0 \end{array} \right], p_3 = \left[ \begin{array}{} 3 \\ 1 \\ 1 \end{array} \right] \in U$$

The vector equation above tells us that every element in ${\rm im \hspace{3pt}}A$ is a linear combination of $p_1,p_2,p_3$.

There is more: these $x_1,x_2,x_3$ are arbitrary, so we have this representation:

$$v=x_1p_1=x_2p_2+x_3p_3,$$

with arbitrary $x_1,x_2,x_3$! Hence

$${\rm im \hspace{3pt}}A = {\rm span}\{p_1,p_2,p_3\}.$$

It seems that we have found the basis. Are we done?

No, we need to check for linear independence.

What if it's not linearly independent? Then what?

Use the Reduction Theorem.

Lesson: We use the columns that correspond to the leading ones in reduced row echelon form.

Example above: Continue:

$\left[ \begin{array}{ccc|c} 1 & 0 & 2 & v_1 \\ 0 & 1 & 1 & v_2 \\ 0 & 0 & 0 & v_3 \end{array} \right]$

$$p_1 = \left[ \begin{array}{} 1 \\ 0 \\ 0 \end{array} \right], p_2 = \left[ \begin{array}{} 0 \\ 1 \\ 0 \end{array} \right], p_3 = \left[ \begin{array}{} 2 \\ 1 \\ 0 \end{array} \right] \rightarrow {\rm span}\{p_1,p_2,p_3\} \neq {\bf R}^3$$

So, they are linearly dependent. Therefore we can choose $\{p_1,p_2\}$ as a basis.

Homework:

• 1. Given a vector space $V$, define $V^* = \{A \colon V \rightarrow {\bf R} {\rm \hspace{3pt} linear}\}$, dual of $V$. Prove this is a vector space.
• 2. Prove that $V^*$ is isomorphic to $V$.