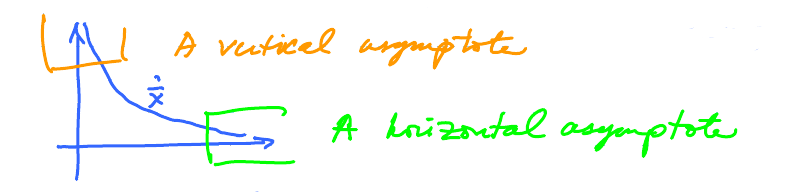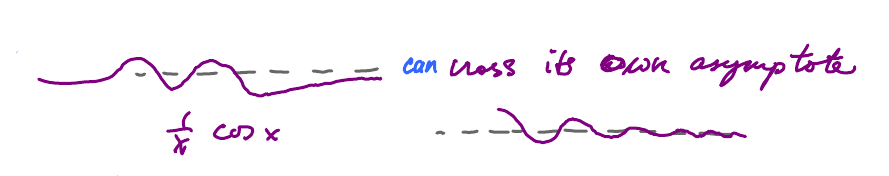Limits at infinity: part 1

"A limit at infinity"

Given $$ y = f(x) $$

Note: Not the same as "infinite limits"

• "Infinite limit" means that $y \to \infty$.
• "Limit at infinity" means that $x \to \infty$.

There are similarities however.

Let's compare.

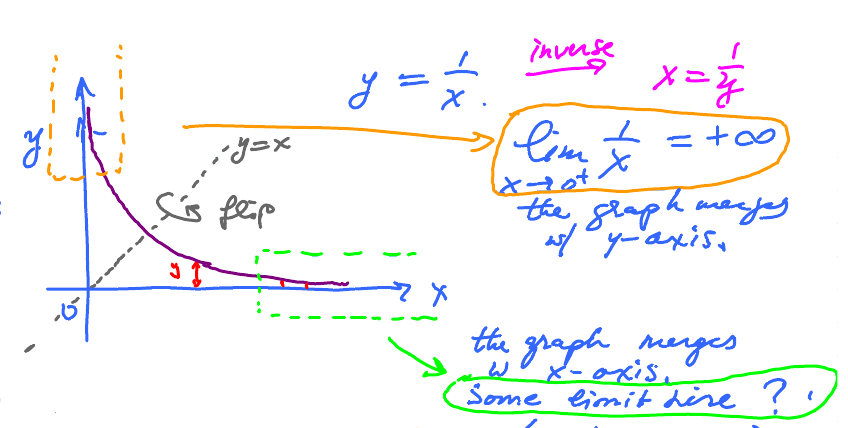
Consider what happens when we take the inverse of a function.

Compare what is happening:

• $\color{orange} x \to 0^{+} \quad y \to +\infty $
• $\color{green} y \to 0^{+} \quad x \to +\infty$

Rewrite the second one $$\lim_{x \to +\infty}\frac{1}{x} = 0 $$ a limit at $\infty$, i.e. $x$ approaches $\infty$.

Notation similar to the old $$\lim_{x \to 1} \frac{1}{x} = 1 $$ "$x$" approaches 1. What is the main difference?

• $\lim\limits_{x \to a}$, a number, is about the local/short term behavior of the function.\
• $\lim\limits_{x \to \infty}$, is about the long term behavior.

Example. Recall the gravitational force: $$F = \gamma \frac{m_{1} m_{2}}{d^{2}},$$ where $m_{1}$, $m_{2}$ are masses of the two objects and $d$ is distance between them.

Let $d$ be the variable. Then $$ \lim_{d \to \infty} F = 0.$$ This means that the force becomes negligible as you move away.

Numerical comparison:

$x$	1	10	100	1000	10,000	$\rightarrow$	$\infty$
$\frac{1}{x}$	1	0.1	0.01	0.001	0.0001	$\rightarrow$	0

Graphical comparison:

Let's make this more precise the geometry behind this algebra.

Definition. Suppose $$\lim_{x \to \infty} f(x) = L,$$ then we say that $y = L$ is a horizontal asymptote.

Remember this is a straight line.

Suppose $f$ is one-to-one and $y = L$ is its horizontal asymptote.

Question 

What about $f^{-1}$?

Answer 

$ y = L$ is a vertical asymptote of $x = f^{-1}(y)$.

And vice versa!

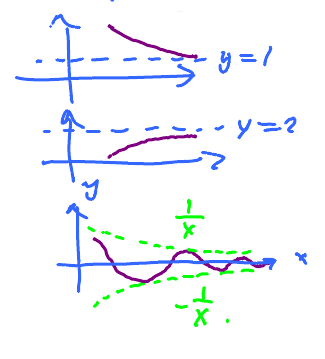
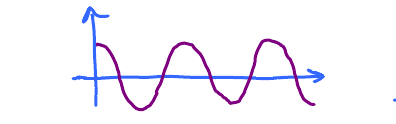
Example. Very simple... $$\begin{gathered} \lim_{x \to \infty} \left(1 + \frac{1}{x}\right) = 1 \\ \lim_{x \to +\infty} \left(2 - \frac{1}{x}\right) = 2 \\ \lim_{x \to +\infty} \frac{1}{x}\cos x = 0 \end{gathered}$$

Summary:

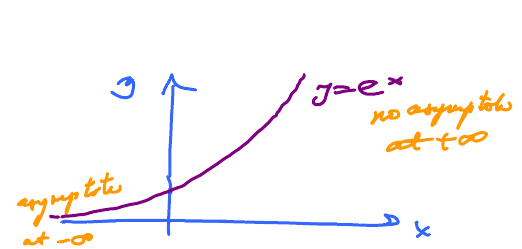
Example. Given $$\begin{gathered} f(x) = e^{x} \\ \lim_{x \to \infty} e^{x} = ? \\ \lim_{x \to -\infty} e^{x} = 0 \\ \lim_{x \to +\infty} e^{x} = +\infty \end{gathered}$$

Graphically:

Recall the possible outcomes for a limit at a point: $$\lim_{x \to a} f(x) = \begin{cases} \text{ exists, } L \text{ a number} \\ \infty \\ \text{ does not exist (even as } \infty) \end{cases}$$ Same for: $$\lim_{x \to \pm\infty} f(x) $$

Example. $$\lim_{x \to \infty} \cos x $$ does not exist. Why?

Informally, we say that no single value $L$ is approached by the value $f(x)$ function as $x$ approaches $\infty$.

Fact: All rules of limits hold for limits at $\infty$.

Recall that $f$ is continuous at $x=a$ if $\lim\limits_{x \to a} f(x) = f(a)$. (Definition)

To prove discontinuity, show the opposite: $$ \lim_{x\to a} f(x) \neq f(a) $$ Three possibilities:

1. $\lim\limits_{x\to a} f(x)$ does not exist.
2. $f(a)$ is not defined.
3. They are not equal.

Example. Let's fully investigate this function: $$f(x) = \begin{cases} \frac{x^{2} - x}{x^{2} - 1} & \text{ if } x \neq 1 \\ 1 & \text{ if } x = 1 \end{cases}$$

1. Is $f(1)$ defined? Yes, $f(1) = 1$
2. Does the limit exist? Let's compute it.

$$\lim_{x\to 1} f(x) = \lim_{x \to 1} \frac{x^{2} - x}{x^{2} - 1}$$ Plug in $x=1$. $$\frac{1^{1} - 1}{1^{2} - 1} = \frac{0}{0}$$ Indeterminate!

So, we need to do algebra before limit.

$$\begin{aligned} \lim_{x \to 1} \frac{x^{2} - x}{x^{2} - 1} & = \lim_{x \to 1} \frac{x(x-1)}{(x-1)(x+1)} \\ & = \lim_{x \to 1} \frac{x}{x+1} \\ &= \frac{1}{1 + 1} = \frac{1}{2} \end{aligned}$$ Note that $\frac{x}{x+1}$ is rational and continuous on its domain

Are the limits equal?

No. $1 \neq \frac{1}{2}$. That's why the function is discontinuous at this point (removable).

Formula: $$f(x) = \begin{cases} \frac{x}{x+1} & \text{ if } x \neq 1 \\ 1 & \text{ if } x = 1 \end{cases}$$

Find the domain: $$\begin{aligned} x + 1 & \neq 0 \\ x \neq 1 \end{aligned}$$

Domain: $$(-\infty,-1) \cup(-1,\infty)$$

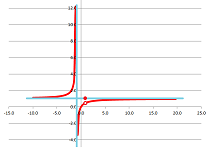
Consider $\frac{x}{x+1}$ at $x=-1$: $$\lim\limits_{x \to -1}\frac{x}{x+1}$$ is infinite $(=\infty)$, so $x=-1$ is a vertical asymptote.

However there are still 4 distinct possibilities of how the graph approaches the asymptote.

To tell which one, compute the one-sided limits: $$\begin{aligned} \lim_{x \to -1^{-}} \frac{x}{x+1} \left( = \frac{-}{-} = + \right) & = +\infty \\ \lim_{x \to -1^{+}} \frac{x}{x+1} \left( = \frac{-}{+} = - \right) & = -\infty \end{aligned}$$

Next, behavior at $\infty$. $$\lim_{x \to \infty} f(x) = \lim_{x \to \infty} \frac{x}{x+1} = 1 \gets \frac{1000000}{1000001} \text{ informally}$$ So $y=1$ is a horizontal asymptote.

Finally, plot it:

$\square$

This was: Algebra $\rightarrow$ Graph
Sometimes: Graph $\rightarrow$ Algebra (later)

Q: Can the graph of a function cross its own asymptote?

Example.

That's $ \frac{1}{x}\cos x$.

A: Yes.

Proceed to Limits at infinity: part 2.