Limits: transition from discrete to continuous

Limits of sequences: large scale trends

A function defined on a ray in the set of integers, $\{p,p+1,...\}$, is called an (infinite) sequence.

Instead of $$f(x)=1/x,$$ the preferred notation is $$a_n=\{a_n=1/n:\ n=1,2,3,...\},$$ with the abbreviated notation on the left. In fact, we will assume that the values of the sequence are on the $x$-axis.

The main, if not the only, reason for studying sequences is to see their trends.

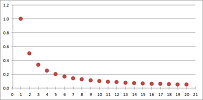
The main, go-to, example is that of the sequence of the reciprocals: $$x_n=\frac{1}{n}.$$ It tends to $0$.

It is easy to confirm numerically: $$x_n=1.000, 0.500, 0.333, 0.250, 0.200, 0.167, 0.143, 0.125, 0.111,... $$

Also, for any fixed real number, we can easily construct a sequence that tends to that number -- via its decimal approximations. For example, $$x_n=0.3 , 0.33 , 0.333 , 0.3333 , . . . \text{ tends to } 1 / 3 .$$

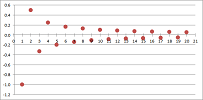
The values can also approach the ultimate destination from both sides, such as $$x_n=(-1)^n\frac{1}{n}.$$

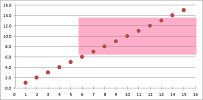
Geometrically, we see the trend because we can enclose the end of the tail of the sequence in a band:

It should be, in fact, a narrower and narrower band.

Algebraically, we see that for every measure of closeness $\varepsilon$, the function's values become eventually that close to the limit.

Definition. We call number $a$ the limit of the sequence $a_n$ if the following condition holds:

• for each real number $\varepsilon > 0$, there exists a natural number $N$ such that, for every natural number $n > N$, we have

$$|a_n - a| < \varepsilon .$$ If a sequence has limit, then we call it convergent and say that it converges; otherwise it is divergent and we say it diverges.

The limit notation is $$a_n \to a \text{ as } n\to \infty,$$ as well as $$\lim_{n\to\infty} a_n=a.$$

Examples of divergence are below.

A sequence may tend to infinity, such as $x_n=n$:

Then no band -- no matter how wide -- will contain the sequence's tail.

This behavior however has a meaningful pattern.

Definition. We say that a sequence $a_n$ tends to positive infinity if the following condition holds:

• for each real number $R $, there exists a natural number $N$ such that, for every natural number $n > N$, we have

$$a_n >R .$$ We say that a sequence $a_n$ tends to negative infinity if:

• for each real number $R $, there exists a natural number $N$ such that, for every natural number $n > N$, we have

$$a_n <R .$$

We describe such a behavior with the following notation: $$a_n\to \pm\infty \text{ as } n\to \infty \ \text{ or }\ \lim_{n\to \infty}a_n=\pm\infty.$$

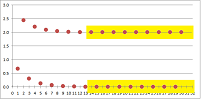
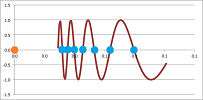
Some sequences seem to have no pattern at all, such as $x_n=\sin n$:

Here, a band -- if narrow enough -- can contain the sequence's tail.

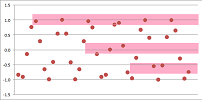
The next example is $x_n=1+(-1)^n+\frac{1}{n}$. It seems to approach two limits at the same time:

Indeed, no matter how narrow, we can find two bands to contain the sequence's two tails. However, no single band -- if narrow enough -- will contain them!

Theorem (Uniqueness). A sequence can have only one limit.

Thus, there can be no two limits and we are justified to speak of the limit.

Algebraic properties of limits of sequences

Limits behave well with respect to the usual arithmetic operations. Below we assume that the sequences are defined on the same set of integers.

We will study convergence of sequence with the help of other, simpler, sequences. The theorem below shows why.

Theorem. $$a_n\to a \ \Longleftrightarrow\ |a_n-a|\to 0.$$

Then to understand limits of sequences in general, we need first to understand those of a smaller class:

• positive sequences that converge to $0$.

The definition of convergence becomes simpler:

• $0<a_n\to 0$ when for any $\varepsilon >0$ there is $N$ such that $a_n<\varepsilon $ for all $n>N$.

We start with addition.

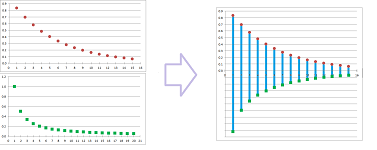
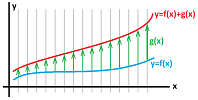
To graphically add two sequences, we flip the second upside down and then connect each pair of dots with a bar. Then, the lengths of these bars form the new sequence. Now, if either sequence converges to $0$, then so do these bars.

Theorem (Sum Rule). $$0<a_n\to 0,\ 0<b_n\to 0 \ \Longrightarrow\ a_n+ b_n\to 0.$$

Proof. Suppose $\varepsilon >0$ is given. From the definition,

• $a_n\to 0\ \Longrightarrow$ there is $N$ such that $a_n<\varepsilon /2$ for all $n>N$, and
• $b_n\to 0\ \Longrightarrow$ there is $M$ such that $b_n<\varepsilon /2$ for all $n>M$.

Then for all $n>\max\{N,M\}$, we have $$a_n+b_n<\varepsilon /2+\varepsilon /2 =\varepsilon .$$ Therefore, by definition $a_n+ b_n\to 0$. $\blacksquare$

Multiplying a sequence by a constant number simply stretches the whole picture in the vertical direction.

However, zero remains zero!

Theorem (Constant Multiple Rule). $$0<a_n\to 0 \ \Longrightarrow\ ca_n\to 0 \text{ for any real }c>0.$$

Proof. Suppose $\varepsilon >0$ is given. From the definition,

• $0 < a_n\to 0\ \Longrightarrow$ there is $N$ such that $a_n <\varepsilon /c$ for all $n>N$.

Then for all $n>N$, we have $$c\cdot a_n < c\cdot \varepsilon /c=\varepsilon .$$ Therefore, by definition $ca_n\to 0$. $\blacksquare$

For more complex situations we need to use the fact that convergent sequences are bounded; i.e., the sequence fits into a (not necessary narrow) bar.

Theorem (Boundedness). $$a_n\to a \ \Longrightarrow\ |a_n| < Q \text{ for some real } Q.$$

Proof. Choose $\varepsilon =1$. Then by definition, there is such $N$ that for all $n>N$ we have: $$|a_n-a| < 1.$$ Then, we have $$\begin{array}{lll} |a_n|&=|(a_n-a)+a|&\text{ ...then by the Triangle Inequality...}\\ &\le |a_n-a|+|a|&\text{ ...then by the inequality above...}\\ &<1+|a|. \end{array}$$ To finish the proof, we choose: $$Q=\max\{|a_1|,...,|a_N|,1+|a|\}.$$ $\blacksquare$

The proof is illustrated below:

We are now ready for the general results on the algebra of limits.

Theorem (Sum Rule). If sequences $a_n ,b_n$ converge then so does $a_n + b_n$, and $$\lim_{n\to\infty} (a_n + b_n) = \lim_{n\to\infty} a_n + \lim_{n\to\infty} b_n.$$

Proof. Suppose $$a_n\to a,\ b_n\to b.$$ Then $$|a_n - a|\to 0, \ |b_n-b|\to 0.$$ We compute $$\begin{array}{lll} |(a_n + b_n)-(a+b)|&= |(a_n-a)+( b_n-b)|& \text{ ...then by the Triangle Inequality...}\\ &\le |a_n-a|+| b_n-b|&\\ &\to 0+0 & \text{ ...by SR...}\\ &=0. \end{array}$$ Then, by the last theorem, we have $$|(a_n + b_n)-(a+b)|\to 0.$$ Then, by the first theorem, we have: $$a_n + b_n\to a+b.$$ $\blacksquare$

When two sequences are multiplied, it is as if we use each pair of their values to build a rectangle:

Then the areas of these rectangles form a new sequence and these areas converge if the widths and the heights converge.

Theorem (Product Rule). If sequences $a_n ,b_n$ converge then so does $a_n \cdot b_n$, and $$\lim_{n\to\infty} (a_n \cdot b_n) = (\lim_{n\to\infty} a_n)\cdot( \lim_{n\to\infty} b_n).$$

Proof. Suppose $a_n\to a,\ b_n\to b$. Then, $$|a_n-1|\to 0,\ |b_n-b|\to 0.$$ Consider, $$\begin{array}{lll} |a_n\cdot b_n-a\cdot b| &= |a_n\cdot b_n+(-a\cdot b_n+a\cdot b_n) -a\cdot b|&\text{ ...adding extra terms then factoring...}\\ &= |(a_n-a)\cdot b_n+a\cdot( b_n - b)|&\text{ ...then by the Triangle Inequality...}\\ &\le |(a_n-a)\cdot b_n|+|a\cdot ( b_n - b)|&\\ &= |a_n-a|\cdot |b_n|+|a|\cdot | b_n - b|&\text{ ...then by Boundedness...}\\ &\le |a_n-a|\cdot Q+|a|\cdot | b_n - b|&\\ &\to 0\cdot Q+|a|\cdot 0&\text{ ...by SR and CMR...}\\ &=0. \end{array}$$ Therefore, $$a_n\cdot b_n \to a\cdot b.$$ $\blacksquare$

CMR follows.

Theorem (Constant Multiple Rule). If sequence $a_n $ converges then so does $c a_n$ for any real $c$, and $$\lim_{n\to\infty} c\, a_n = c \cdot \lim_{n\to\infty} a_n.$$

One can understand division of sequences as multiplication in reverse: if the areas of the rectangles converge and so do their widths, then so do their heights.

Theorem (Quotient Rule). If sequences $a_n ,b_n$ converge then so does $a_n / b_n$ whenever defined, and $$\lim_{n\to\infty} \left(\frac{a_n}{b_n}\right) = \frac{\lim\limits_{n\to\infty} a_n}{\lim\limits_{n\to\infty} b_n},$$ provided $\lim_{n\to\infty} b_n \ne 0.$

Proof. We will only prove the case of $a_n=1$. Suppose $b_n\to b\ne 0$. First, choose $\varepsilon =|b|/2$ in the definition of convergence. Then there is $N$ such that for all $n>N$ we have $$|b_n-b|<|b|/2.$$ Therefore, $$|b_n|>|b|/2.$$ Next, $$\begin{array}{lll} \left| \frac{1}{b_n}-\frac{1}{b} \right| &= \left|\frac{b-b_n}{b_nb} \right|&\\ &= \frac{|b-b_n|}{|b_n|\cdot|b|}&\text{ ...then by above inequality...}\\ &< \frac{|b-b_n|}{|b/2|\cdot|b|}&\\ &\to \frac{0}{|b/2|\cdot|b|}&\text{ ...by the CMR...}\\ &=0. \end{array}$$ Therefore, $$\frac{1}{b_n} \to \frac{1}{b}.$$ Finally, the general case of QR follows from PR: $$\frac{a_n}{b_n}=a_n\cdot \frac{1}{b_n}.$$ $\blacksquare$

An application of PR in a simple situation reveals a new shortcut: $$\begin{array}{lll} \lim_{n\to \infty} \big( a_n \big)^2 &=\lim_{n\to \infty} \left( a_n\cdot a_n \right)\\ &=\lim_{n\to \infty} a_n\cdot \lim_{n\to \infty}a_n \\ &=\left(\lim_{n\to \infty} a_n\right)^2, \end{array}$$ provided that limit exists. A repeated use of PR produces a more general formula.

Theorem (Composition Rule). If sequences $a_n ,b_n$ converge then so does $(a_n)^p$ for any positive integer $p$, and $$\lim_{n\to\infty} \left[ (a_n)^p \right] = \left[ \lim_{n\to\infty} a_n \right]^p.$$

Then, we conclude that limits behave well with respect to composition with some functions.

More properties of limits of sequences

Only the tail of the sequence matters for convergence:

Theorem. A sequence is convergent if and only if its truncations are convergent: $$\{a_n:n=p,p+1,...\}\to a \ \Longleftrightarrow\ \{a_n:n=p+1,p+2,...\}\to a.$$

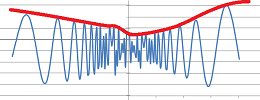
Theorem (Comparison). $$0<a_n\le b_n\to 0 \ \Longrightarrow\ a_n \to 0.$$

Proof. Suppose $\varepsilon >0$ is given. Then, from the definition, we have:

• $b_n\to 0\ \Longrightarrow$ there is $N$ such that $b_n<\varepsilon $ for all $n>N$.

Therefore,

• $a_n\le b_n<\varepsilon $ for all $n>N\quad \Longrightarrow a_n\to 0$.

$\blacksquare$

Theorem. If a sequence is bounded and monotonic then it is convergent.

The construction is used to study not sequences but functions!

Theorem. If $a_n \leq b_n$ for all $n$ greater than some $N$, then $$\lim_{n\to\infty} a_n \leq \lim_{n\to\infty} b_n, $$ provided the sequences converge.

Lemma. If

• $0<a_n\to 0$ and $0<b_n\to 0$,

then

• $\min\{a_n,b_n\}\to 0$ and $\max\{a_n,b_n\}\to 0$.

Proof.

$\blacksquare$

Theorem (Squeeze theorem). If $$a_n \leq c_n \leq b_n \text{ for all } n > N,$$ and $$\lim_{n\to\infty} a_n = \lim_{n\to\infty} b_n = c,$$ then the sequence $c_n$ converges and $$\lim_{n\to\infty} c_n = c.$$

Proof. As we know,

• $a_n\to c$ means $|a_n-c|\to 0$, and
• $b_n\to c$ means $|b_n-c|\to 0$.

From the inequalities we have for all $n > N$: $$a_n-c \le c_n-c \le b_n-c.$$ $\blacksquare$

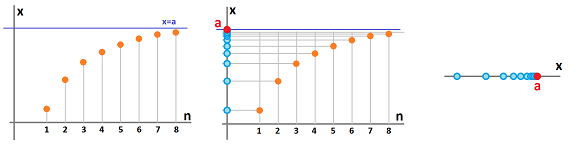
A more compact way to visualize sequences is as sequences of points on the $x$-axis:

New sequences are produces via compositions with functions. Given a sequence $a_n$ and a function $y=f(x)$, define $$b_n=f(a_n).$$

We will use this construction to study functions, next.

Limits of functions: small scale trends

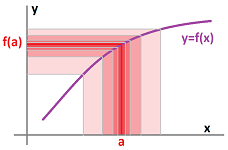
We now concentrate on a small scale behavior of a function; we zoom in on a single point of its graph. Can we say anything about it even if the function $f$ is undefined at a point $a$?

And we would still want to understand what is happening to $f(x)$ when $x$ is in the vicinity of $a$. In order to understand the idea of behavior of a function around a point we use what we do understand: the behavior of sequences around infinity.

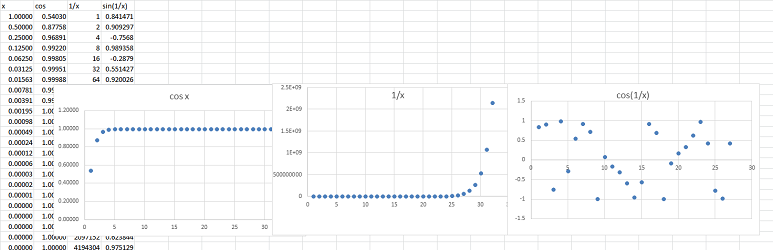
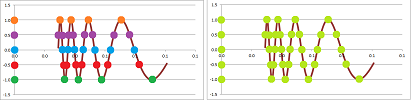
Suppose we would like to study these three functions around the point $a=0$: $$f(x)=\cos x,\ g(x)=\frac{1}{x},\ h(x)=\sin (1/x).$$ Recall that the composition of any function and a sequence gives us a new sequence. Let apply the reciprocal sequence to all three: $$x_n=1/n\to 0.$$

This is what we discover about these three sequences if we explore them numerically:

Here we can see the following: $$\lim_{n\to \infty}\cos (1/n)=1,\ \lim_{n\to \infty}\frac{1}{1/n}=\infty,\ \lim_{n\to \infty}\sin(1/n) \text{ diverges}.$$

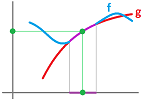
Compare the results to the graphs of these functions:

Our sequence was able to capture the behavior of each function.

One sequence might not be enough though! Indeed, observe the following failure of the sequence $x_n=1/n$: $$\lim_{x\to 0} \operatorname{sign}(x) \text{ doesn't exist but }\lim_{n\to \infty} \operatorname{sign}(1/n)=1,$$ because we approach $0$ from one direction.

Another failure is of the sequence $x_n=\frac{1}{\pi n}$ where $\frac{1}{n}$ succeeded: $$\lim_{x\to 0} \sin(1/x) \text{ doesn't exist but }\lim_{n\to \infty} \sin\frac{1}{x_n}=\lim_{n\to \infty} \sin(\pi n)=\lim_{n\to \infty}0=0.$$

The solution to this problem comes from compositions of the function with all sequences that converge to $a$.

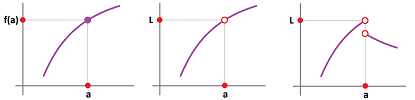
Definition. The limit of a function $f$ at a point $x=a$ is defined to be the limit $$\lim_{x\to a} f(x):=\lim_{n\to \infty} f(x_n),$$ for any sequence $x_n$ within the domain of $f$ excluding $a$ that converges to $a$, $$a\ne x_n\to a \text{ as } n\to \infty,$$ when all these limits exist and are equal to each other. Otherwise, the limit does not exist.

In particular, let's consider the alternating reciprocal sequence and apply it to $y=\operatorname{sign}(x)$: $$x_n=(-1)^n\frac{1}{n}.$$

Then, $$\operatorname{sign}(x_n)=\begin{cases} 1&\text{ if } x \text{ is even},\\ -1&\text{ if } x \text{ is odd}. \end{cases}$$ This sequence is divergent. Therefore, the definition fails, and $\lim_{x\to 0} \operatorname{sign}(x)$ doesn't exist.

Another way to come to this conclusion is to concentrate on one side at a time: $$\begin{array}{ll} \lim_{n\to \infty} \operatorname{sign}\left( -\frac{1}{n} \right)=&\lim_{n\to \infty}-1&=-1 ,\\ \lim_{n\to \infty} \operatorname{sign} \left( \frac{1}{n} \right)=&\lim_{n\to \infty} 1&=1. \end{array}$$ The two limits are different, the definition fails, and that's why $\lim_{x\to 0} \operatorname{sign}(x)$ doesn't exist.

However, the last result also reveals that the behavior of $y=\operatorname{sign}(x)$ on the left and on the right, when considered separately, is very regular. Indeed, we can choose any sequences and, as long as they stay on one side of $0$, we have the same conclusion:

• if $x_n\to 0$ and $x_n<0$ for all $n$, then $\lim_{n\to \infty} \operatorname{sign}(x_n)=-1$, and
• if $x_n\to 0$ and $x_n>0$ for all $n$, then $\lim_{n\to \infty} \operatorname{sign}(x_n)=1$.

Definition. The limit from the left of a function $f$ at a point $x=a$ is defined to be the limit $$\lim_{x\to a^-} f(x):=\lim_{n\to \infty} f(x_n),$$ for any sequence $x_n$ with $$x_n\to a \text{ as } n\to \infty, \text{ and } x_n<a \text{ for all } n,$$ when all these limits exist and are equal to each other. The limit from the right of a function $f$ at a point $x=a$ is defined to be the limit $$\lim_{x\to a^+} f(x):=\lim_{n\to \infty} f(x_n),$$ for any sequence $x_n$ with $$x_n\to a \text{ as } n\to \infty, \text{ and } x_n>a \text{ for all } n,$$ when all these limits exist and are equal to each other. Otherwise, the left/right limit does not exist.

For the “two-sided” limit, the question becomes, do the two -- left and right -- match?

Theorem. The limit of a function $f$ at a point $x=a$ exists if and only if the limits from the left and from the right of $f$ at $x=a$ exist and are equal to each other. Then $$\lim_{x\to a} f(x)=\lim_{x\to a^+} f(x)=\lim_{x\to a^-} f(x).$$

As we know, the limit of sequence is fully determined by its tail. Therefore, the limit of a function at $a$ is fully determined by the tail of the sequence $f(x_n)$ when $x_n\to a$. It follows then that only the behavior of $f$ in the vicinity, no matter how small, of $a$ affects the value (and the existence) of the limit $\lim_{x\to a} f(x)$.

Theorem (Locality). Suppose two functions $f$ and $g$ coincide in the vicinity of point $a$: $$f(x)=g(x) \text{ for all } a-\varepsilon <x <a+\varepsilon,$$ for some $\varepsilon >0$ Then, their limits at $a$ coincide too: $$\lim_{x\to a} f(x) =\lim_{x\to a} g(x).$$

Algebraic properties of limits of functions

We will use the algebraic properties of the limits of sequences to prove virtually identical facts about limits of functions.

Let's re-write the main algebraic properties using the alternative notation.

Theorem (Algebra of Limits of Sequences). Suppose $a_n\to a$ and $b_n\to b$. Then $$\begin{array}{|ll|ll|} \hline \text{SR: }& a_n + b_n\to a + b& \text{CMR: }& c\cdot a_n\to ca& \text{ for any real }c\\ \text{PR: }& a_n \cdot b_n\to ab& \text{QR: }& a_n/b_n\to a/b &\text{ provided }b\ne 0\\ \hline \end{array}$$

Each property is matched by its analog for functions.

Theorem (Algebra of Limits of Functions). Suppose $f(x)\to F$ and $g(x)\to G$ as $x\to a$. Then $$\begin{array}{|ll|ll|} \hline \text{SR: }& f(x)+g(x)\to F+G & \text{CMR: }& c\cdot f(x)\to cF& \text{ for any real }c\\ \text{PR: }& f(x)\cdot g(x)\to FG& \text{QR: }& f(x)/g(x)\to F/G &\text{ provided }b\ne 0\\ \hline \end{array}$$

Let's consider them one by one.

Now, limits behave well with respect to the usual arithmetic operations.

Theorem (Sum Rule). If the limits at $a$ of functions $f(x) ,g(x)$ exist then so does that of their sum, $f(x) \pm g(x)$, and the limit of the sum is equal to the sum of the limits: $$\lim_{x\to a} (f(x) + g(x)) = \lim_{x\to a} f(x) + \lim_{x\to a} g(x).$$

Proof. For any sequence $x_n\to a$, we have by SR: $$\lim_{x\to a} (f(x) + g(x)) = \lim_{n\to \infty} (f(x_n)+g(x_n)) = \lim_{n\to \infty} f(x_n)+\lim_{n\to \infty} g(x_n).$$ $\blacksquare$

The proofs of the rest of the properties are identical.

Theorem (Constant Multiple Rule). If the limit at $a$ of function $f(x)$ exists then so does that of its multiple, $c f(x)$, and the limit of the multiple is equal to the multiple of the limit: $$\lim_{x\to a} c f(x) = c \cdot \lim_{x\to a} f(x).$$

Theorem (Product Rule). If the limits at $a$ of functions $f(x) ,g(x)$ exist then so does that of their product, $f(x) \cdot g(x)$, and the limit of the product is equal to the product of the limits: $$\lim_{x\to a} (f(x) \cdot g(x)) = (\lim_{x\to a} f(x))\cdot( \lim_{x\to a} g(x)).$$

Let's set $g(x)=c$ in PR and use CR, then $$\lim_{x\to a} c f(x)= \lim_{x\to a} (f(x) \cdot g(x)) = c\cdot( \lim_{x\to a} g(x)).$$ Then CMR follows. Even though CMR is absorbed into PR, the former is simpler and easier to use.

Theorem (Quotient Rule). If the limits at $a$ of functions $f(x) ,g(x)$ exist then so does that of their ratio, $f(x) / g(x)$, provided $\lim_{x\to a} g(x) \ne 0$, and the limit of the ratio is equal to the ratio of the limits: $$\lim_{x\to a} \left(\frac{f(x)}{g(x)}\right) = \frac{\lim\limits_{x\to a} f(x)}{\lim\limits_{x\to a} g(x)}.$$

The main building blocks are these two functions with simple limits.

Theorem (Constant). For any real $c$, the following limit exists at any point $a$: $$\lim_{x\to a} c = c.$$

Proof. For any sequence $x_n\to a$, we have $$\lim_{x\to a} c = \lim_{n\to \infty} c = c.$$ $\blacksquare$

Theorem (Identity). The following limit exists at any point $a$: $$\lim_{x\to a} x = a.$$

Proof. For any sequence $x_n\to a$, we have $$\lim_{x\to a} x = \lim_{n\to \infty} x_n = a.$$ $\blacksquare$

Any polynomial can be built from $x$ and constants by multiplication and addition. Therefore, the fist five theorems allow us to compute the limits of all polynomials.

Example. Let $$f(x)=x^3+3x^2-7x+8.$$ What is its limit as $x\to 1$? The computation is straightforward but every step has to be justified with the rules above.

To understand which rules to apply first, observe that the last operation is addition. We use SR first: $$\begin{array}{lll} \lim_{x\to 1}f(x)&=\lim_{x\to 1} (x^3+3x^2-7x+8) &\text{ ...then by SR, we have...}\\ &=\lim_{x\to 1} x^3+\lim_{x\to 1}3x^2-\lim_{x\to 1}7x+\lim_{x\to 1}8 &\text{ ...then using }\\ &\quad\quad \text{ PR, } \quad\quad \text{ CMR, } \quad \text{ CMR, } \quad \text{ CR}, &\text{ we have... }\\ &=\lim_{x\to 1} x \cdot\lim_{x\to 1} x^2+3\lim_{x\to 1}x^2-7\lim_{x\to 1}x+8 \quad&\text{ ...then by IR, we have...}\\ &=1\cdot\lim_{x\to 1} x^2+3\lim_{x\to 1}x^2-7\cdot 1+8 \quad&\text{ ...then by PR and IR, we have...}\\ &=1 \cdot 1 +3 \cdot 1 -7+8\\ &=5. \end{array}$$ $\square$

With this complex argument, it is easy to miss the simple fact that the limit of this function happens to be equal to its value: $$\lim_{x\to 1}f(x)=\lim_{x\to 1} (x^3+3x^2-7x+8)=x^3+3x^2-7x+8\Big|_{x=1}=1^3+3\cdot 1^2-7\cdot 1+8 =5.$$ The idea is confirmed by the plot:

Definition. A function $f$ is called continuous at point $a$ if

• $f(x)$ is defined at $x=a$,
• the limit of $f$ exists at $a$, and
• the two are equal to each other:

$$\lim_{x\to a}f(x)=f(a).$$

Thus, the limits of continuous functions can be found by substitution.

Now rational functions...

Example. Let's find the limit at $2$ of $$f(x)=\frac{x+1}{x-1}.$$ Again, we look at the last operation of the function. It is division, so we use QR first: $$\begin{array}{lll} \lim_{x\to 2}f(x)&=\lim_{x\to 2}\frac{x+1}{x-1}&\text{...we now justify QR by observing that }\\ && \lim_{x\to 2}(x-1)=1\ne 0, \text{ then...}\\ &=\frac{\lim_{x\to 2}(x+1)}{\lim_{x\to 2}(x-1)}\\ &=\frac{3}{1}\\ &=3. \end{array}$$ $\square$

Example. Let's find the limit at $1$ of the function $$f(x)=\frac{x^2-1}{x-1}.$$ Since the last operation is division, so are supposed to use QR first. However, the limit of the denominator is $0$: $$\lim_{x\to 1}(x-1)=0.$$ Then, QR is inapplicable. But then all other rules of limits are also inapplicable!

A closer look reveals that things are even worse; both the numerator and the denominator go to $0$ as $x$ goes to $1$. An attempt to apply QR -- over these objections -- would result in an indeterminate expression: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{ll}\frac{x^2-1}{x-1}& \ra{???}& \frac{0}{0}\text{ as } x\to 1.\end{array}$$ This doesn't mean that the limit doesn't exist; we just need to get rid of the indeterminacy. The answer is algebra.

We factor the numerator and then cancel the denominator (thereby circumventing the need for QR): $$\begin{array}{lll} \lim_{x\to 1}f(x)&=\lim_{x\to 1}\frac{x^2-1}{x-1}\\ &=\lim_{x\to 1}\frac{(x-1)(x+1)}{x-1}\\ &=\lim_{x\to 1}(x+1) \\ &=2. \end{array}$$ The cancellation is justified by the fact that $x$ tends to $1$ but never reaches it. $\square$

Example. Let's consider more examples of how trying to apply the laws of limits without verifying their conditions could lead to indeterminate expressions. We choose a few algebraically trivial situations.

First, for $x\to 0$, a misapplication of QR leads to the following: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{ll}\frac{x^2}{x}& \ra{???}& \frac{0}{0},&\text{ instead of }\frac{x^2}{x}=x\to 0.\end{array}$$ We now discover how the same indeterminate expression has a different outcome: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{ll}\frac{x}{x^2}& \ra{???}& \frac{0}{0},&\text{ instead of }\frac{x}{x^2}=\frac{1}{x}\to \infty.\end{array}$$

Now, there are other kinds of indeterminate expressions. For $x\to \infty$, a misapplication of QR leads to the following: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{ll}\frac{x^2}{x}& \ra{???}& \frac{\infty}{\infty},&\text{ instead of }\frac{x^2}{x}=x\to \infty.\end{array}$$ The same indeterminate expression has a different outcome: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{ll}\frac{x}{x^2}& \ra{???}& \frac{\infty}{\infty},&\text{ instead of }\frac{x}{x^2}=\frac{1}{x}\to 0.\end{array}$$

Finally, we see how indeterminate expressions appear under SR instead of QR. For $x\to \infty$, we have the following: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{ll} (x+1)-x & \ra{???}& \infty -\infty,&\text{ instead of }(x+1)-x =1.\end{array}$$ $\square$

Continuous functions

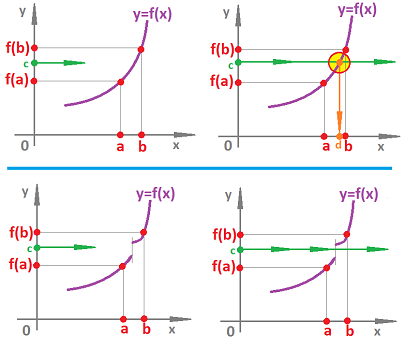
This what we mean by a continuous dependence of $y$ on $x$ under function $f$:

• a small deviation of $x$ from $a$ produces a small deviation of $y=f(x)$ from $f(a)$:

We can see below such an example:

Such dependencies are ubiquitous in nature:

• the location of a moving object continuously depends on time,
• the pressure in a close container continuously depends on the temperature,
• the air resistance continuously depends on the velocity of the moving object, etc.

It is our goal to develop this idea in full rigor and to make sure that our mathematical tools match the perceived reality.

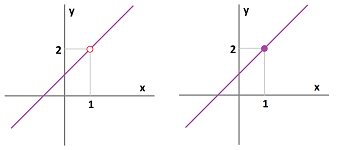
Consider these two functions: $$f(x)=\frac{x^2-1}{x-1} \text{ and } g(x)=x+1.$$ The limit of the former is found by this computation: $$\begin{array}{lll} \lim_{x\to 1}f(x)&=\lim_{x\to 1}\frac{x^2-1}{x-1}\\ &=\lim_{x\to 1}\frac{(x-1)(x+1)}{x-1}\\ &=\lim_{x\to 1}(x+1) \\ &=2, \end{array}$$ while that of the latter by a direct substitution: $$\lim_{x\to 1}g(x)=\lim_{x\to 1}(x+1)=x+1\Big|_{x=1}=1+1=2,$$ because it is continuous.

The two functions are almost the same and the difference is seen in their graphs below:

There is only one point missing from the former graph. However, if we think of the graph of a function as a rope, we realize that the former graph is cut into two pieces! The latter is a single piece. It is indeed “continuous”.

The former graph is easy to “repair” by adding a single point. There are other, more extreme, cases of discontinuity.

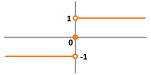
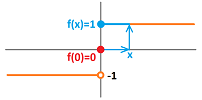
Example. The sign function $f(x)=\operatorname{sign}(x)$ has a visible gap at $x=0$:

This example shows how the idea of continuous dependence of $y$ on $x$ fails: starting with $x=0$, even a tiniest deviation of $x$, say, $x=.0001$, produces a jump in $y$ from $\operatorname{sign}(0)=0$ to $\operatorname{sign}(.0001)=1$. $\square$

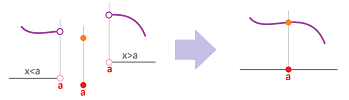
The example teaches us a lesson. Given a function $f$ and a point $a$, where $f$ is defined, the graph of $f$ consists of three parts:

• 1. the part of the graph of $f$ with $x<a$,
• 2. the part of the graph of $f$ with $x=a$ (one point), and
• 3. the part of the graph of $f$ with $x>a$.

For this function to be continuous, these three parts have to fit together:

We put this idea in the form of a theorem that relies on the concept of a one-sided limit.

Theorem. A function $f$ is continuous at $x=a$ if and only if $f$ is defined at $a$, the two one-sided limits exist and both equal to the value of the function at $a$; $$\lim_{x\to a^-}f(x)=f(a)=\lim_{x\to a^+}f(x).$$

Even more extreme examples are below.

Example. The reciprocal function $g(x)=1/x$ has an infinite gap at $x=0$:

Here, if the deviations of $x$ from $0$ differ in sign, the jump in $y$ may be very large: from $\frac{1}{-.0001}=-10000$ to $\frac{1}{.0001}=10000$. $\square$

Example. The sine of the reciprocal $g(x)=\sin \left( 1/x \right)$ oscillates infinitely many times as we approach $0$:

Here, a deviation of $x$ from $0$ may unpredictably produce any number between $-1$ and $1$. $\square$

Now the good news:

• a typical function we encounter is continuous at every point of its domain.

Theorem.

• Every polynomial is continuous at every point.
• Every rational function is continuous at every point where it is defined.

The theorem follows from the following algebraic result.

Theorem. Suppose $f$ and $g$ are continuous at $x=a$. Then so is

• 1. (SR) $f\pm g$,
• 2. (CMR) $c\cdot f$ for any real $c$,
• 3. (PR) $f \cdot g$, and
• 4. (QR) $f/g$ provided $g(a)\ne 0$.

Proof. For SR, we compute the following: $$\begin{array}{lll} \lim_{x\to a} \big( (f+g)(x) \big) &=\lim_{x\to a} \left( f(x)+ g(x) \right) & \text{ ...by SR for limits...}\\ &=\lim_{x\to a} f(x)+ \lim_{x\to a} g(x) &\text{ ...by continuity...}\\ &=f(a)+g(a)\\ &=(f+g)(a). \end{array}$$ Therefore, $f+g$ is continuous by the definition. Next, CMR, PR, and QR are proved with CMR, PR, and QR for limits, respectively. $\square$

In SR, $g$ serves as a, non-constant but continuous, push of the rope that is the graph of $f$:

In addition we can say that if the floor and the ceiling ($f$ and $g$) of a tunnel are changing continuously then so is its height ($g-f$).

In CMR, $c$ is the magnitude of a vertical stretch/shrink of the rubber sheet that has the graph of $f$ drawn on it.

In PR, we say that if the width and the height ($f$ and $g$) of a rectangle are changing continuously then so is its area ($f\cdot g$):

To justify our conclusion about polynomials, let's consider a general representation of an $n$th degree polynomial: $$a_0+a_1x+a_2x^2+...+a_{n-1}x+a_nx^n,$$ and follow these steps: $$\begin{array}{lrrrrr} \text{these are continuous: }&1,&x,&x,&...&x,&x;\\ \text{these are too by PR: }&1,&x,&x^2,&...&x^{n-1},&x^n;\\ \text{these too by CMR: }&a_0,&a_1x,&a_2x^2,&...&a_{n-1}x^{n-1},&a_nx^n;\\ \text{this is continuous by SR: }&a_0&+a_1x&+a_2x^2&+...&+a_{n-1}x^{n-1}&+a_nx^n. \end{array}$$

Continuity and compositions

An application of PR in a simple situation reveals a new shortcut: $$\begin{array}{lll} \lim_{x\to a} \big( f(x) \big)^2 &=\lim_{x\to a} \left( f(x)\cdot f(x) \right)\\ &=\lim_{x\to a} f(x)\cdot \lim_{x\to a} f(x) \\ &=\left(\lim_{x\to a} f(x)\right)^2, \end{array}$$ provided that limit exists. Then, furthermore, a repeated use of PR produces a more general formula: $$\lim_{x\to a} f(x)^n = \left[ \lim_{x\to a} f(x) \right]^n,$$ for any natural number $n$. Thus, the limit of the power is equal to the power of the limit.

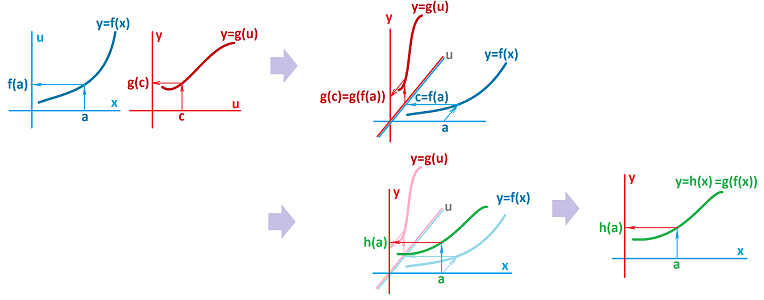
The conclusion is, in fact, about compositions of functions. Indeed, above we have: $$f(x)^n =g(f(x)) \text{ with } g(u)=u^n.$$ What is so special about this new function? It is continuous!

Theorem (Composition Rule). If the limit at $a$ of function $f(x)$ exists and is equal to $L$ then so does that of its composition with any function $g$ continuous at $L$ and $$\lim_{x\to a} (g\circ f)(x) = g\left( \lim_{x\to a} f(x) \right).$$

Proof. Suppose $x_n\to a$. Then, $$\begin{array}{lll} \lim_{x\to a} (g\circ f)(x) &= \lim_{n\to \infty} (g\circ f)(x_n)\\ & = \lim_{n\to \infty} g(f(x_n))&\\ &= g\left( L \right), \end{array}$$ since $f(x_n)\to L$ and $g$ is continuous. Now, as the result is independent of a choice of $x_n$, we conclude that the limit exists. $\blacksquare$

In other words, the continuous $g$ is moved out of the limit to be computed. In a sense, the limit is, again, computed by substitution.

Corollary. The composition $g\circ f$ of a function $f(x)$ continuous at $a$ and a function $g$ continuous at $f(a)$ is continuous at $a$.

The composition is illustrated below:

One can see now how the two continuous functions interact. First, we have their continuity described separately:

• 1. a small deviation of $x$ from $a$ produces a small deviation of $u=f(x)$ from $f(a)$, and
• 2. a small deviation of $u$ from $c$ produces a small deviation of $y=g(u)$ from $g(c)$.

If we set $c=f(a)$, we have:

• 3. a small deviation of $u=f(x)$ from $c=f(a)$ produces a small deviation of $y=g(u)=g(f(x))$ from $g(c)=g(f(a))$.

That's continuity of $h=g\circ f$ at $x=a$!

Example. Consider these two functions and their composition $$\begin{array}{ll} y=g(u)&=u^2+2u-1,\\ u=f(x)&=2x^{-3}. \end{array}$$ What is the limit of $h=g\circ f$ at $1$?

First, we note that $g$ is continuous at every point as a polynomial. Therefore, by the theorem we have: $$\lim_{x\to 1} (g\circ f)(x) = g\left( \lim_{x\to 1} f(x) \right),$$ if the limit on the right exists. It does, because $f$ is a rational function defined at $x=1$: $$\lim_{x\to 1} f(x)=\lim_{x\to 1} 2x^{-3} =2\cdot 1^{-3}=2.$$ The limit becomes a number, $u=2$, and this number we substitute into $g$: $$\lim_{x\to 1} h(x) = g\left( \lim_{x\to 1} f(x) \right)=g(2)=2^2+2\cdot 2-1=7.$$

The answer is verified by a direct computation of $h$: $$h(x)=(g\circ f)(x) = g(f(x))=u^2+2u-1\Big|_{u=2x^{-3}}=\left( 2x^{-3} \right)^2+2\left( 2x^{-3} \right)-1=4x^{-6} +4x^{-3} -1.$$ Since the function is continuous (rational and defined at $1$), we have by substitution: $$\lim_{x\to 1} h(x)=4x^{-6} +4x^{-3} -1\Big|_{x=1}=4\cdot 1^{-6} +4\cdot 1^{-3} -1=7.$$ $\square$

We compute limits by verifying and then using, via CR, the continuity of the functions involved.

Example. Compute: $$\lim_{x\to 0} \frac{1}{\left( x^2+x-1 \right)^3}.$$

We proceed by a gradual decomposition of $$r(x)= \frac{1}{\left( x^2+x-1 \right)^3}.$$ The last operation of $f$ is division. Therefore, $$r(x)=g(f(x)),\text{ where } u=f(x)=\left( x^2+x-1 \right)^3 \text{ and }g(u)=\frac{1}{u}.$$ Function $g$ is rational; but is it continuous? Its denominator isn't zero at the point we are interested in: $$f(0)=\left( x^2+x-1 \right)^3\Big|_{x=0}=\left( 0^2+0-1 \right)^3=-1\ne 0.$$ Then CR applies and our limit becomes: $$\lim_{x\to 0} \frac{1}{\left( x^2+x-1 \right)^3}=\lim_{x\to 0} r(x)=\lim_{x\to 0} g(f(x))=g(\lim_{x\to 0}f(x))=\frac{1}{\lim_{x\to 0}\left[ \left( x^2+x-1 \right)^3\right]},$$ provided the new limit exits. Notice that the limit to be computed has been simplified!

Let's compute it. We start over and continue with a decomposition of $$p(x)= \left( x^2+x-1 \right)^3.$$ The last operation of $f$ is the power. Therefore, $$p(x)=g(f(x)),\text{ where } u=f(x)=x^2+x-1 \text{ and }g(u)=u^3.$$ Function $g$ is a polynomial and, therefore, continuous. Then CR applies and the limit becomes: $$\lim_{x\to 0} \left( x^2+x-1 \right)^3=\lim_{x\to 0} p(x)=\lim_{x\to 0} g(f(x))=g(\lim_{x\to 0}f(x))=\left[ \lim_{x\to 0}\left( x^2+x-1\right) \right]^3,$$ provided the new limit exits. Notice that, again, the limit to be computed has been simplified!

Let's compute it. We realize that the function $x^2+x-1$ is a polynomial and, therefore, its limit is computed by substitution: $$\lim_{x\to 0} \left( x^2+x-1\right) =x^2+x-1\Big|_{x=0}=0^2+0-1=-1.$$

What remains is to combine the three formulas above: $$\begin{array}{lll} \lim_{x\to 0} \frac{1}{\left( x^2+x-1 \right)^3}&=\frac{1}{\left[\lim_{x\to 0}\left( x^2+x-1 \right)^3 \right]}\\ &=\frac{1}{\left[ \lim_{x\to 0}\left( x^2+x-1 \right) \right]^3}\\ &=\frac{1}{\left[ -1 \right]^3}\\ &=-1. \end{array}$$ $\square$

When there is no continuity to use, we may have to apply algebra (such as factoring), or trigonometry, etc. in order to find another decomposition of the function.

So far, the only kind of function we know to be continuous is the rational functions: all algebraic operations, including compositions, of rational functions produce more rational functions. The continuity of even such a simple function as the square root $f(x)=\sqrt{x}$ remains unproven. But the inverse of this function is a polynomial!

Recall that functions are inverses when one undoes the effect of the other; for example,

• the multiplication by $3$ is undone by the division by $3$, and vice versa;
• the second power is undone by the square root (for $x\ge 0$), and vice versa;
• the exponential function is undone by the logarithm of the same base, and vice versa, etc.

More precisely, they undo each other under composition; two functions $y=f(x)$ and $x=g(y)$ are called inverse of each other when for all $x$ in the domain of $f$ and for all $y$ in the domain of $g$, we have: $$g(f(x))=x \text{ and } f(g(y))=y.$$

Every function $y=f(x)$ which is one-to-one (i.e., there is only one $x$ for each $y$) has the inverse $x=g(y)$ which is also one-to-one (i.e., there is only one $y$ for each $x$). If we take the graph of the former and flip this piece of paper so that the $x$-axis and the $y$-axis are interchanged, we get the graph of the latter (and vice versa):

The shapes of the graphs are the same; in fact, it's the same graph! It is then conceivable that the continuity of one implies the continuity of the other.

Theorem. The inverse of a function $y=f(x)$ continuous at $x=a$, if exists, is a function $x=g(y)$ continuous at $y=f(a)$.

Proof. $\blacksquare$

Thus, not only the rational functions are continuous (within their domains) but also their inverses. In particular, we have $$\lim_{x\to a} \sqrt{f(x)} = \sqrt{ \lim_{x\to a} f(x) }.$$

More on limits and continuity

To show continuity of functions beyond the rational functions, we will imply some indirect and direct methods.

Theorem (Comparison). Non-strict inequalities between functions are preserved under limits, i.e., if $$f(x) \leq g(x)$$ for all $n$ greater than some $N$, then $$\lim_{x\to a} f(x) \leq \lim_{x\to a} g(x), $$ provided the limits exist.

Observe that replacing the non-strict inequality, $$f(x) \leq g(x), $$ with a strict one, $$f(x) < g(x) ,$$ won't produce a strict inequality in the conclusion of the theorem.

From such an inequality, we can't conclude anything about the existence of the limit:

Having two inequalities, on both sides, may work better.

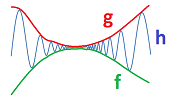
It is called a squeeze. If we can squeeze out function between two familiar functions, we might be able to say something about its limit. Some further requirements will be necessary.

Theorem (Squeeze Theorem). If a function is squeezed between two functions with the same limit at a point, its limit also exists and is equal to the that number; i.e., if $$f(x) \leq h(x) \leq g(x) ,$$ for all $n$ greater than some $N$, and $$\lim_{x\to a} f(x) = \lim_{x\to a} g(x) = L,$$ then the following limit exists and equal to that number: $$\lim_{x\to a} h(x) = L.$$

Proof. For any sequence $x_n\to a$, we have: $$f(x_n) \leq h(x_n) \leq g(x_n).$$ We also have $$\lim_{n\to \infty} f(x_n) = \lim_{n\to \infty} g(x_n) = L.$$ Therefore, by the Squeeze Theorem for sequences we have $$\lim_{n\to \infty} h(x_n) = L.$$ $\blacksquare$

The squeeze theorem is also known as the Two Policemen Theorem: if two policemen are escorting a prisoner (handcuffed) between them, and both officers go to the same(!) police station, then -- in spite of some freedom the handcuffs allow -- the prisoner will also end up in that station.

Another name is the Sandwich Theorem. It is, once again, about control. A sandwich can be a messy affair: ham, cheese, lattice, etc. One won't want to touch that and instead takes control of the contents by keeping them between the two buns. He then brings the two to his mouth and the rest of the sandwich along with them!

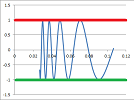
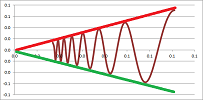
Example. Let's find the limit, $$\lim_{x \to 0}x \sin(\tfrac{1}{x}).$$

It cannot be computed by PR because $$\lim_{x\to 0}\sin(\tfrac{1}{x})$$ does not exist. Let's try a squeeze. This is what we know fromtrigonometry: $$-1 \le \sin(\tfrac{1}{x}) \le 1. $$ Note that this squeeze proves nothing about the limit of $\sin(\tfrac{1}{x})$:

Let's try another squeeze: $$-|x| \le x \sin(\tfrac{1}{x}) \le |x| .$$

Now, since $\lim_{x\to 0}(-x) =\lim_{x\to 0}(x)=0$, by the Squeeze Theorem, we have: $$\lim_{x\to 0} x \sin(\tfrac{1}{x})=0.$$ $\square$

What about the continuity of trigonometric functions? Let's review.

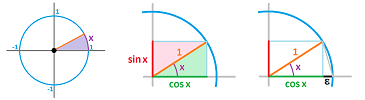
Suppose a real number $x$ is given. We construct a line segment of length $1$ on the plane. Then

• $\cos x$ is the projection of the segment on the horizontal line,
• $\sin x$ is the projection of the segment on the vertical line.

It is as though $\cos x$ is the length of the shadow of the stick on the ground when the sun is above and $\sin x$ is the length of its shadow on the wall at sunset...

It is then plausible that -- as the stick rotates -- the length of the shadow changes continuously. To prove that we will assume the continuity of $\sin$ and $\cos$ at one single point, $x=0$.

Lemma. $$\lim_{x\to 0} \sin x = 0 \text{ and } \lim_{x\to 0} \cos x = 1.$$

Theorem. Both $\cos$ and $\sin$ are continuous.

Proof. Consider: $$\begin{array}{lll} \lim_{h \to 0} \sin(a + h) &= \lim_{h \to 0} \left( \sin a \cdot \cos h + \cos a \cdot \sin h \right)&\text{ ...by a trig formula...}\\ &= \lim_{h \to 0} \left(\sin a \cdot \cos h\right) + \lim_{h \to 0} \left(\cos a \cdot \sin h\right) &\text{ ...by SR...}\\ &= \sin a \cdot \lim_{h \to 0} \cos h + \cos a \cdot \lim_{h \to 0} \sin h &\text{ ...by CMR...}\\ &= \sin a \cdot 1 + \cos a \cdot 0 &\text{ ...by the lemma...}\\ &= \sin a . \end{array}$$ From trigonometry, we know that $$\cos(x)=\sin(\pi/2-x).$$ Therefore, $\cos$ is also continuous as the composition of these continuous functions. $\blacksquare$

The theorem confirms that the graphs of $\sin$ and $\cos$ do indeed look like this, even if we zoom in on any point:

Example. The first of the two important limits: $$\lim_{x\to 0} \frac{\sin x}{x} =1, \ \lim_{x\to 0} \frac{1 - \cos x}{x} = 0.$$ follows by the Squeeze Theorem from this trigonometric fact: $$\cos x \le \frac{\sin x}{x} \le 1.$$ $\square$

We would like to conclude that the inverses of $\sin$ and $\cos$ are also continuous. However, neither function is one-to-one. What we did with $y=x^2$ vs. $x=\sqrt{x}$ and will repeat here is:

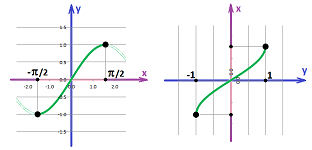
• restrict the domain of the function to be able to define its inverse.

We choose the branch of $\sin$ over $-\pi/2 \le x \le \pi/2$. Thus, we have a pair of inverse functions, the sine (restricted) and the arcsine: $$y=\sin x,\ x\in [-\pi/2,\pi/2], \text{ and } x=\sin^{-1}y,\ y\in [-1,1].$$

The graphs are of course the same with just $x$ and $y$ interchanged. Similarly, we choose the branch of $\cos$ over $0 \le x \le \pi$. Thus, we have a pair of inverse functions, the cosine (restricted) and the arccosine: $$y=\cos x,\ x\in [0,\pi], \text{ and } x=\cos^{-1}y,\ y\in [-1,1].$$

What about the tangent?

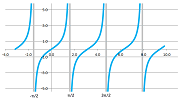
Recall its definition: $$\tan x =\frac{\sin x}{\cos x}.$$ By QR, it is continuous at every point $x$ with $\cos x\ne 0$. Let's consider one such point, $x=\pi/2$. We know that, as $x\to \pi/2$, we have $$\sin x\to 1 \text{ and } \cos x\to 0.$$ We should conclude that $$\tan x\to \pm\infty.$$ However, which infinity? We take into account the sign of $\cos x$ on the two sides of $\pi/2$: $$0<\cos x\to 0 \text{ as } x\to \pi/2^- \text{ and } 0>\cos x\to 0 \text{ as } x\to \pi/2^+.$$ Therefore, $$\tan x\to +\infty \text{ as } x\to \pi/2^- \text{ and } \tan x\to -\infty \text{ as } x\to \pi/2^+,$$ and, indeed, the graph reveals different behavior on the two sides of $\pi/2$. The pattern repeats itself every $\pi$ units on the $x$-axis.

We consider more examples of such behavior below.

Global properties of continuous functions

Recall that a function $f$ is called bounded on interval $[a,b]$ if there is such a real number $Q$ that $$|f(x)| \le Q$$ for all $x$ in $[a,b]$.

Theorem. If the limit at $x=a$ of function $f$ exists then $f$ is bounded on some interval that contains $a$: $$\lim_{x\to a}f(x) \text{ exists }\ \Longrightarrow\ |f(x)| \le Q$$ for all $x$ in $[a-\delta,a+\delta]$ for some $\delta >0$ and some $Q$.

We have been speaking so far of continuity only one point at a time: there is no cut at $x=a$.

Definition. A function $f$ is called continuous on interval $(A,B)$ if it is continuous at every point in $(A,B)$. It if continuous when the interval is $(-\infty,\infty )$.

Then, in particular, $1/x$ is continuous on $(-\infty,0)$ and on $(0,\infty )$.

A more advanced than the one above result is the following.

Theorem. A continuous on interval $[a,b]$ function is bounded on $[a,b]$.

Our understanding of continuity of functions is as ones with no gaps in their graphs. It is more precisely expressed by the following.

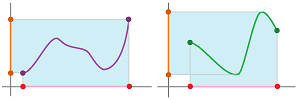
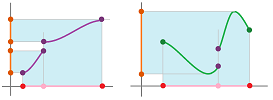
Theorem (Intermediate Value Theorem). Suppose a function $f$ is defined and is continuous on interval $[a,b]$. Then for any $c$ between $f(a)$ and $f(b)$, there is $d$ in $[a,b]$ such that $f(d) = c$.

In other words, we can get from point $A=f(a)$ to point $B=f(b)$ without having to jump. We can see in the second part of the illustration how this property may fail.

Corollary. If the domain of a continuous function is an interval then so is its range.

This is how discontinuity may cause the range to have gaps:

The last graph shows that the converse of the theorem isn't true.

Choosing $c=0$ in the theorem gives us the following.

Corollary. If a continuous on interval function $f$ has the opposite signs at the end-points of $[a,b]$: $$f(a)>0,\ f(b)<0 \text{ or } f(a)<0,\ f(b)>0,$$ then $f$ has an $x$-intercept between $a$ and $b$.

Large-scale behavior: asymptotes

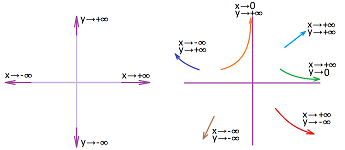
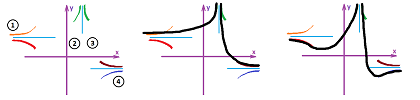
Graphs of most functions are infinite and won't fit into any piece of paper. Then they have to leave the paper and do that in a number of different ways:

We just have to look at $x$ and $y$ separately to determine the trend of the point $(x,y)$ in the plane. For example,

• if $x\to +\infty$ and $y\to 0^+$, then we have: $(x,y) \searrow$;
• if $x\to 3^+$ and $y\to -\infty$, then we have: $(x,y) \swarrow$; etc.

As the point however approaches the line it can't cross ($y=0$ and $x=3$ in the above examples), the curve starts to become more and more straight and almost(!) merge with that line. The line is then called an asymptote.

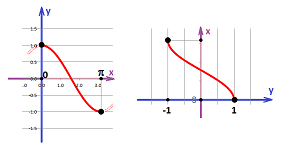
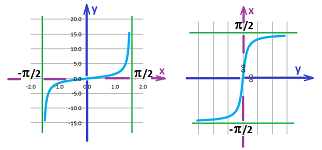
Example. As an illustration we will consider the tangent $y=\tan x$ and its inverse, arctangent. Just as $\sin$ and $\cos$ however $\tan$ isn't one-to-one. Once again we have to restrict the domain of the function to be able to define its inverse. We choose the branch of $\tan$ over $-\pi/2 <x < \pi/2$. Thus, we have a pair of inverse functions, the tangent (restricted) and the arctangent: $$y=\tan x,\ x\in (-\pi/2,\pi/2), \text{ and } x=\tan^{-1}y.$$

The graphs are of course the same with just $x$ and $y$ interchanged.

Let's describe their large-scale behavior with limits. First the tangent: $$\tan x\to-\infty \text{ as } x\to -\pi/2^+ \text{ and } \tan x\to+\infty \text{ as } x\to \pi/2^-.$$ In other words, $$x\to -\pi/2^+,\ y\to-\infty \text{ and } x\to \pi/2^-,\ y\to+\infty.$$ Changing $x$ to be the dependent and $y$ to be the independent variables, we simply re-write the above for the arctangent: $$\tan^{-1} y\to-\pi/2^+ \text{ as } y\to -\infty \text{ and } \tan^{-1} y\to\pi/2^- \text{ as } y\to +\infty.$$ $\square$

Definition. Given a function $y=f(x)$, a line $y=a$ for some real $a$ is called a horizontal asymptote of $f$ if $$\lim_{x\to -\infty}f(x)=a \text{ or } \lim_{x\to +\infty}f(x)=a.$$ A line $x=b$ for some real $b$ is called a vertical asymptote of $f$ if $$\lim_{x\to a^-}f(x)=\pm\infty \text{ or } \lim_{x\to a^+}f(x)=\pm\infty.$$

Naturally, the vertical asymptotes of a function are the horizontal asymptotes of its inverse and vice versa.

Example. Some functions have both kinds: $$f(x)=\frac{1}{x}.$$ Indeed, $y=0$ is its horizontal asymptote (at both ends) and $x=0$ is its vertical asymptote. In more detail: $$\frac{1}{x}\to 0^- \text{ as }x\to -\infty,\ \frac{1}{x}\to 0^+ \text{ as }x\to +\infty, \frac{1}{x}\to -\infty \text{ as }x\to 0^-,\ \frac{1}{x}\to +\infty \text{ as }x\to 0^+.$$ $\square$

Example. Now we approach from the opposite direction: suppose we know the limits, plot the asymptotes and a possible graph of the function.

Suppose this is what we know about $f$: it is defined for all $x\ne 3$, and $$\lim_{x\to 3}f(x)=+\infty,\ \lim_{x\to -\infty}f(x)=3,\ \lim_{x\to =\infty}f(x)=-2.$$ Let's rewrite those:

• 1. $x\to -\infty,\ y\to 3$;
• 2. $x\to 3^-,\ y\to +\infty$;
• 3. $x\to 3^+,\ y\to +\infty$;
• 4. $x\to +\infty,\ y\to -2$.

We draw rough strokes to represent these facts, left:

The ambiguity about how the graph approaches the asymptotes remains at $-\infty$ and $+\infty$. We connect the initial strokes into a single graph (with two branches). Two possible versions of the graph of $f$ are shown on the right. $\square$

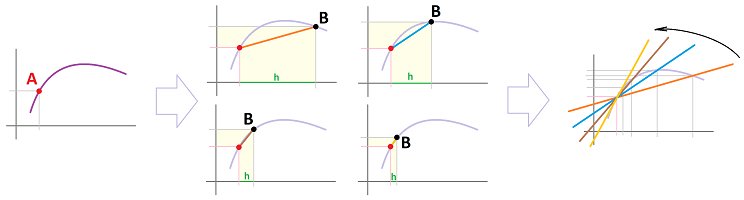
Instantaneous rate of change: the derivative

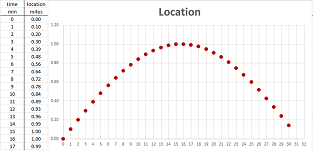
Recall how we estimated the derivative of a node function:

The increment was chosen $h=1$.

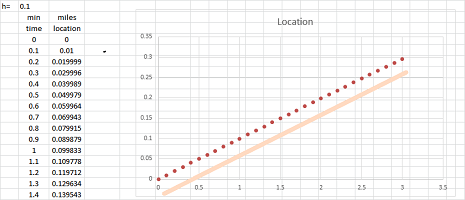
We would like understand the derivative of the sine function that produced this node function in the vicinity of $0$. We choose a smaller step $h=.1$:

We can see an almost straight line!

If we desire an infinite accuracy, we need to consider the limit of these lines as $h\to 0$:

Riemann integrals

This is an abbreviated notation to write these limits: $$\lim_{x \to \infty} \int_a^x f(t) \; dt =\int_a^\infty f(t) \; dt,$$ $$\lim_{x \to -\infty} \int_x^b f(t) \; dt =\int_{-\infty}^b f(t) \; dt.$$

Series

This is an abbreviated notation to write the limit: $$\lim_{n \to \infty} \sum_{i=s}^n f(i) =\sum_{i=s}^\infty f(i).$$