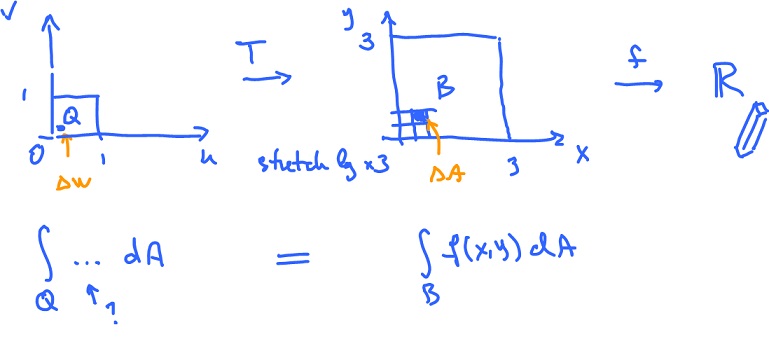This site is being phased out.
Change of variables in integral
Contents
Indefinite integral
techniques of integration...
Definite integral
Consider how we compute this integral in two ways:
$$\displaystyle\int_0^1 2x e^{x^2} dx.$$
In either case we use change of variables.
(1) We use the substitution:
$$u = x^2, du = 2xdx.$$
to compute the antiderivative (with respect to $x$):
$$\displaystyle\int 2x e^{x^2} dx= \displaystyle\int e^u du = e^u + c = e^{x^2} + C,$$
and then apply the Fundamental Theorem of Calculus with respect to $x$:
$$\displaystyle\int_0^1 2x e^{x^2} dx = e^{x^2} |_0^1 = e - 1.$$
(2) Alternatively, we use the same substitution to get
$$\displaystyle\int_{x=0}^{x=1} 2x e^{x^2} dx = \displaystyle\int_{u=0}^{u=1} e^u du $$
but don't do "the back-substitution" and then apply the Fundamental Theorem of Calculus with respect to $u$:
$$= \displaystyle\int_0^1 e^u du $$ $$= e^u |_0^1 $$ $$= e^1 - e^0.$$
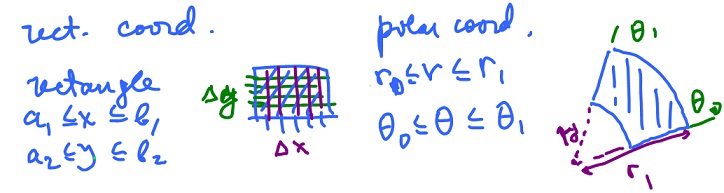
Definite integral in polar coordinates
We want to utilize the geometry of polar coordinate system to make integration over some (curved) regions simpler.
Let' start with 2D Cartesian coordinates. We integrate over a rectangle:
$$a_1 {\leq} x {\leq} b_1, a_2 {\leq} y {\leq} b_2.$$
Now, we follow the same procedure with polar coordinates:
$$r_0 {\leq} r {\leq} r_1, {\theta}_0 {\leq} {\theta} {\leq} {\theta}_1$$
The geometry of this "rectangle" is different of course. In fact, we have
To compute
$$\displaystyle\int\displaystyle\int_G f( x, y ) dA $$
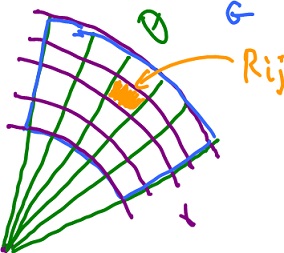
in polar coordinates (volume under the graph) we need some kind of Riemann sum. What we do exactly mimics the rectangular case, but only algebraically:
- divide $[ {\theta}_0, {\theta}_1 ]$ into $k$ intervals,
- length ${\Delta}{\theta}$,
- divide $[ r_0, r_1 ]$ into $k$ intervals,
- length ${\Delta}r$,
- evaluate $f( r_i, {\theta}_j )$ with each $( r_i, {\theta}_j )$ in $R_{ij}$.
Then the Riemann sum is
$$\displaystyle\sum_{i=1}^k \displaystyle\sum_{j=1}^k f( r_i, {\theta}_j ) {\Delta}A,$$
where ${\Delta}A$ is the area of the rectangle $R_{ij}$.
Approximate the volume by the sum of these volumes,
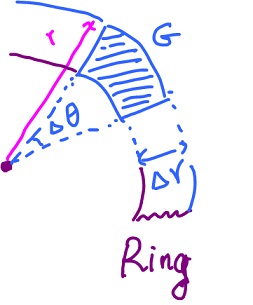
We compute the area of the curved rectangle with sides ${\Delta}r, {\Delta}{\theta}$, which varies with the location (unlike rectangular). How? Consider a circle with radius $r$ and area ${\pi}r^2$, and another circle with radius $r - {\Delta}r$ and area ${\pi}( r - {\Delta}r )^2$. Then we obtain a ring with area
$$\begin{array}{} {\pi}r^2 - {\pi}( r - {\Delta}r )^2 &= {\pi}( r^2 - ( r - {\Delta}r )^2 ) \\ &= {\pi}( 2r - {\Delta}r ) {\Delta}r \\ &= ( r - \frac{{\Delta}r}{2} ) {\Delta}r {\Delta}{\theta}. \end{array}$$
"Rectangle", $R$, the area is equal the the area of a ring multiplied by $\frac{{\Delta}{\theta}}{2{\pi}}$, hence
The total volume is approximated by the Riemann sum
$$\begin{array}{} \displaystyle\sum_{i,j}^k f( r_i, {\theta}_j ) ( r - \frac{{\Delta}r}{2} ) {\Delta}r {\Delta}{\theta} &= ... \\ &= \lim_{k \rightarrow \infty} \displaystyle\sum_{i,j}^k f( r_i, {\theta}_j ) ( r - \frac{{\Delta}r}{2} ) {\Delta}r {\Delta}{\theta} \\ &= \displaystyle\int_{\theta_0}^{\theta_1} \displaystyle\int_{r_0}^{r_1} f( r, {\theta} ) r dr d{\theta}. \end{array}$$
Example. Compute the volume of the half-sphere
$$\displaystyle\int\displaystyle\int_D ( 1 - x^2 - y^2 )^{\frac{1}{2}} dA$$
with $D: 0 {\leq} {\theta} {\leq} 2{\pi}, 0 {\leq} r {\leq} 1$. Further
$$g( x, y ) {\rightarrow} f( r, {\theta} ),$$
$$z = ( 1 - x^2 - y^2 )^{\frac{1}{2}} {\rightarrow} ( 1 - ( r \cos {\theta} )^2 - ( \sin {\theta} )^2 )^{\frac{1}{2}} = ( 1 - r^2 )^{\frac{1}{2}}.$$
Then
$$\begin{array}{} V &= \displaystyle\int_{\theta=0}^{\theta = 2 \pi} \displaystyle\int_{r=0}^{r=1} ( 1 - r^2 )^{\frac{1}{2}} r d{\theta} dr &= 2{\pi} \displaystyle\int_0^1 ( 1 - r^2 )^{\frac{1}{2}} r dr. \end{array}$$
Finally, with
$$u = 1 - r^2 , du = -2 r dr$$\
we have
$$\begin{array}{} 2{\pi} \displaystyle\int_0^1 u^{\frac{1}{2}} ( -1 / 2 ) du &= \frac{2{\pi}}{2} \cdot \frac{2}{3} \cdot u^{\frac{3}{2}} |_0^1 \\ &= \frac{2}{3} \cdot {\pi}. \end{array}$$
Example. Compute the area of a circle:
$A =$ the volume under the graph of $f( x, y ) = 1$.
$$\begin{array}{} A = V &= \displaystyle\int\displaystyle\int_D 1 dA \\ &= \displaystyle\int_0^{2 \pi} \displaystyle\int_0^1 r dr d{\theta} \\ &= \displaystyle\int_0^{2 \pi} \left. \frac{r^2}{2} \right|_0^1 d{\theta} \\ &= \displaystyle\int_0^{2 \pi} \frac{1}{2} d{\theta} \\ &= 2{\pi} \cdot \frac{1}{2} \\ &= {\pi}. \end{array}$$
Note that in
$$\displaystyle\int_Q g( x, y ) dA = \displaystyle\int_R g( r \cos {\theta}, r \sin {\theta} ) r dr d{\theta},$$
$g( r \cos {\theta}, r \sin {\theta} ) r$ is a composition.
Definite integral in dimension $n$
We start with a simple example of alternative Cartesian system.
Let ${\rm \hspace{3pt} dim \hspace{3pt}} = 2$. Compute the integral
$$\displaystyle\int_B f( x, y ) dA$$
with respect to another coordinate system $( u, v )$. This system comes from a transformation
$$( x, y ) = T( u, v )$$
with $T: {\bf R}^2 {\rightarrow} {\bf R}^2$.
The question is: what is the function (of $u,v$) we should integrate over $Q$ to get the same result as integration of $f(x,y)$ over $B = T(Q)$:
$$\displaystyle\int_Q ... dA = \displaystyle\int_B f( x, y ) dA?$$
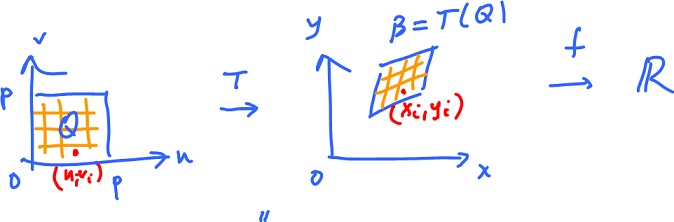
Compare the Riemann sums:
$$\displaystyle\sum_i f( T( u_i, v_i ) ) {\Delta}W =^{!!} \displaystyle\sum_i f( x_i, y_i ) {\Delta}A,$$
where the $u_i$ are the heights, ${\Delta}W$ the areas, the $x_i$ the heights and ${\Delta}A$ the area of the base. Then what is the correspondence:
$$T( u_i, v_i ) {\longleftrightarrow}^? ( x_i, y_i )$$
This is what we do know:
$$9 {\Delta}W {\longleftrightarrow} {\Delta}A$$
Then
$$\displaystyle\sum_i f( T( u_i, v_i ) ) 9 {\Delta}W = \displaystyle\sum_i f( x_i, y_i ) {\Delta}A,$$
where $( 9 {\Delta}W )$ equals ${\Delta}A$. Substitution and the limit and the Riemann sum of $f$, respectively, yield
$$\displaystyle\int_Q f( T( u, v )) 9 dW = \displaystyle\int_B f( x, y ) dA.$$
Where does this 9 come from?
$$T( u, v ) = \left| \begin{array}{} 3 & 0 \\ 0 & 3 \end{array} \right| \left| \begin{array}{} 4 \\ v \end{array} \right|$$
and
$$T' = \left| \begin{array}{} 3 & 0 \\ 0 & 3 \end{array} \right|$$
Then $9 = | {\rm det \hspace{3pt}} T' |$. This is the "stretching coefficient".
Let's consider $| {\rm det \hspace{3pt}} T' |$ in a couple of examples.
Example. Polar coordinates:
$$\displaystyle\int_B f( x, y ) dA = \displaystyle\int\displaystyle\int f( r \cos {\theta}, r \sin {\theta} ) r dr d{\theta},$$
$$T( r, {\theta} ) = ( r \cos {\theta}, r \sin {\theta} )$$
$$T'( r, {\theta} ) = \left| \begin{array}{} \cos \theta & -\sin \theta \\ \sin \theta & r \cos \theta \end{array} \right|$$
and
$$\begin{array}{} | {\rm det \hspace{3pt}} T'( r, {\theta} ) | &= | \cos {\theta} r \cos {\theta} - \sin {\theta} ( -r \sin {\theta} ) | \\ &= | r \cos^2 {\theta} + r \sin^2 {\theta} | \\ &= r | \cos^2 {\theta} + \sin^2 {\theta} | \\ &= r. \end{array}$$
Example. Rotation, rotated through ${\alpha}$
$$T' = \left| \begin{array}{} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array} \right|$$
$${\rm det \hspace{3pt}} T' = \cos^2 {\alpha} + \sin^2 {\alpha} = 1,$$
no stretching.
Review exercise. Consider
$$\displaystyle\int\displaystyle\int_{B(0,1)} x^2 y^2 dA,$$
convert to iterated integral:
$$\displaystyle\int_{-1}^1 \displaystyle\int_{\sqrt{1-x^2}}^{\sqrt{1-x^2}} x^2 y^2 dy dx$$
Consider a more general situation. Suppose
Then
0 \end{array} \right|, v_2 = \left| \begin{array}{} * \\ * \\ 0 \end{array} \right|$
Further
$$v_1 = T( e_1 ), v_2 T( e_2 ).$$
Now
$$T(u,v) = \left| \begin{array}{} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right| \left| \begin{array}{} u \\ v \end{array} \right|$$
then
$$v_1 = T(e_1) = \left| \begin{array}{} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right| \left| \begin{array}{} 1 \\ 0 \end{array} \right| = \left| \begin{array}{} a_{11} \\ a_{21} \end{array} \right|$$
and
$$v_1 = T(e_2) = \left| \begin{array}{} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right| \left| \begin{array}{} 0 \\ 1 \end{array} \right| = \left| \begin{array}{} a_{12} \\ a_{22} \end{array} \right|$$
Substitute:
$$\begin{array}{} {\rm area \hspace{3pt}} B = ||v_1 \times v_2|| &= \left\lVert \begin{array}{ccc} |a_{11}| &\times &|a_{12}| \\ |a_{21}| &\times &|a_{22}| \\ |0| &\times &|0| \end{array} \right\rVert \\ &= \left\lVert {\rm det} \left| \begin{array}{} a_{11} & a_{12} & i \\ a_{21} & a_{22} & j \\ 0 & 0 & k \end{array} \right| \right\rVert \\ &=\lVert 0i + 0j + {\rm det \hspace{3pt}} M_t k \rVert \\ &=| \det M_t|, \end{array}$$
where $M_t$ is the matrix of $T$.
Theorem.
where $T$ is affine, $M_t$ is its matrix, $Q$ the unit square.
Riemann sum of $f$ equals
$$\displaystyle\sum_i f( x_i, y_i ) {\Delta}A,$$
where ${\Delta}A$ are the areas of the parallelograms.
Transform it to the Riemann sum over $( u, v )$
$$\displaystyle\sum_i f( T( u, v_i ) ) | \det T' | {\Delta}W,$$
where ${\Delta}W$ is the area of the squares.
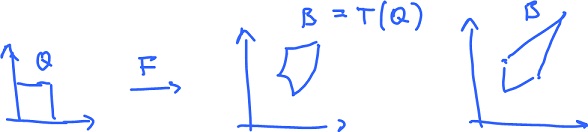
Theorem. If $T$ is an affine function $T: {\bf R}^2 {\rightarrow} {\bf R}^2$, and $Q$ a square, $B = T(Q)$, then
$$\displaystyle\int\displaystyle\int_{B=T(Q)} f( x, y ) dA = \displaystyle\int\displaystyle\int_Q f( T( u, v ) ) | \det T' | dW.$$
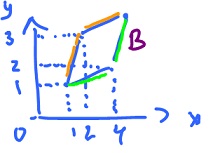
Problem. Suppose $B$ is the parallelogram on the right. Evaluate $\displaystyle\int\displaystyle\int_B x^2 y dA$.
We could solve the problem by applying iterated integral with these bounds as graphs bounding $B$ from below and above. But instead we will simplify $B$, then integrate over $Q$.
How do we transform $B$ into the unit square? We need to find $S: {\bf R}^2 {\rightarrow} {\bf R}^2$ such that
$$S(B) = Q.$$
Turns out $T = S^{-1}$ if
$$T(u,v) = \left| \begin{array}{} 1 & 3 \\ 2 & 1 \end{array} \right| \left| \begin{array}{} u \\ v \end{array} \right| + \left| \begin{array}{} 1 \\ 1 \end{array} \right|.$$
To verify that $T$ is an invertible function, check:
$$\det T \neq 0,$$
Indeed:
$$| \det T | = \left| \begin{array} 1 & 3 \\ 2 & 1 \end{array} \right| = | 1 - 6| = 5.$$
We have $f( x, y ) = x^2 y$ and
$$\displaystyle\int\displaystyle\int_B x^2 y dA = \displaystyle\int\displaystyle\int_Q f T( u, v ) 5 dW {\rm \hspace{3pt} (iterated)}$$
Then $$\begin{array}{} f T(u,v) &= f \left( \left| \begin{array}{} 1 & 3 \\ 2 & 1 \end{array} \right| \left| \begin{array}{} u \\ v \end{array} \right| + \left| \begin{array}{} 1 \\ 1 \end{array} \right| \right) \\ &= f(u + 3v + 1, 2u+v+1 ) \\ &= (u + 3v + 1)^2 (2u+v+1), \end{array}$$
hence
$$\displaystyle\int\displaystyle\int_B x^2 y dA = \displaystyle\int_0^1 \displaystyle\int_0^1 ( u + 3v + 1 )^2 ( 2u + v + 1 ) du dv.$$
The rest of the calculation is routine.
Exercise. A similar example for integration over a disk:
$$\displaystyle\int\displaystyle\int_{B(0,1)} x^2 y^2 dA,$$
with
$$x = r \cos {\theta}$$
$$y = r \sin {\theta}$$
and $| det T' | = r$. Further
$$\begin{array}{} \displaystyle\int_0^{2 \pi} \displaystyle\int_0^1 (r \cos {\theta} )^2 (r \sin {\theta} )^2 r dr d{\theta} &= \displaystyle\int_0^{2 \pi} \displaystyle\int_0^1 r^5 \cos {\theta} \sin {\theta} dr d{\theta} \\ &= \displaystyle\int_0^{2 \pi} \cos^2 {\theta} \sin^2 {\theta} d{\theta} \displaystyle\int_0^1 r^5 dr \\ &= ... \end{array}$$
substitute $u = \sin {\theta}$ and complete the computation.
What if $F$ is not affine?
Then find the best affine approximation $T$ of $F$, at each point $( a, b )$. Which means that
$$F'( a, b ) = T'( a, b ).$$
This approximation applies to every element of the Riemann sum, i.e., on each of the rectangles $R_{ij}$, in total
And the result is:
$$\displaystyle\int\displaystyle\int_{B=T(Q)} f( x, y ) dA = \displaystyle\int\displaystyle\int_Q f( T( u, v )) | \det' T( u, v )| dW.$$