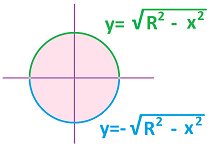This site is being phased out.
Integrals of functions of several variables
Contents
- 1 Volumes and the Riemann sums
- 2 Properties of the Riemann sums
- 3 The Riemann integral over rectangles
- 4 The weight as the 3d Riemann sum
- 5 The weight as the 3d Riemann integral
- 6 Lengths, areas, volumes, and beyond
- 7 Outside the sandbox
- 8 Triple integrals
- 9 The $n$-dimensional case
- 10 The center of mass
- 11 The expected value
- 12 Gravity
Volumes and the Riemann sums
All functions in this chapter are real-valued.
Our understanding of volumes is limited to that of Chapter 13. If $D$ is a region on the plane and it is lifted off the plane to the height $h$ then the cylinder-like solid (a “shell”) between these two plane regions is assumed to have the volume of: $$V=A\cdot h.$$
We furthermore represented more complex solid in terms of these shells.
We will have to start over though.
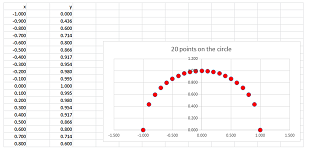
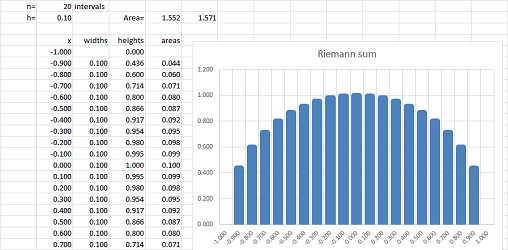
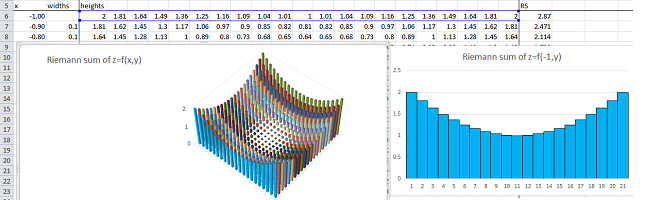
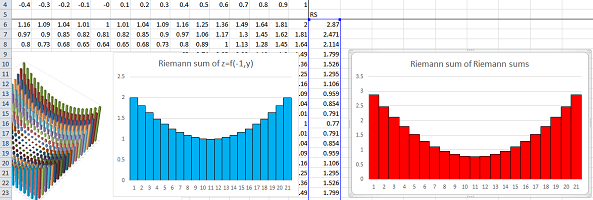
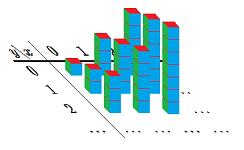
Example. Let's review the Area Problem: we confirm that the area of a circle of radius $1$ is \( A = \pi \). First we plot the graph of $$y=f(x)=\sqrt{1-x^2},\ -1\le x\le 1,$$ with $21$ points ($20$ intervals). We let the values of $x$ run from $-1$ to $1$ every $.1$ and apply the formula: $$\texttt{=SQRT(1-RC3^2)},$$ to get the values of $y$.
We next cover this half-circle with vertical bars based on the interval $[-1,1]$: the bases of the bars are our intervals in the $x$-axis and the heights are values of $y=f(x)$. To see the bars, we simply change the type of the chart plotted by the spreadsheet:
Then the area of the circle is approximated by the sum of the areas of the bars: we multiply the widths of the bars by the heights, place the result in the last column, and finally add all entries in this column. The result $1.552$ is close to $\pi/2\approx 1.571$.
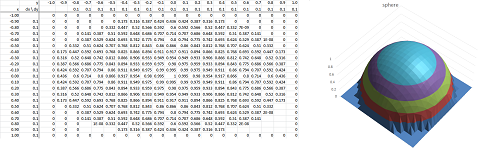
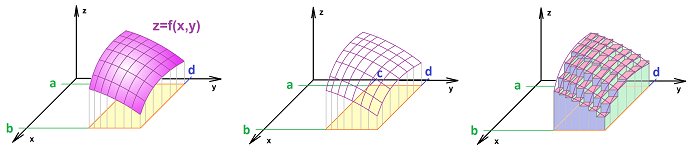
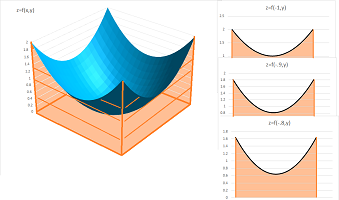
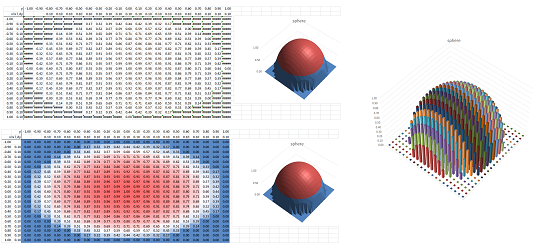
We proceed to the Volume Problem. We will confirm that the volume of a sphere of radius $1$ is \( V = \frac{4}{3}\pi \). First we plot the graph of $$z=f(x,y)=\sqrt{1-x^2-y^2},\ -1\le x\le 1,\ -1\le y\le 1.$$ We recycle our spreadsheet for the sphere. We already have $20$ intervals for $x$ in the first column. Now, just as before, we construct $20$ intervals for $y$ in the first row. We let the values of $x$ and $y$ run from $-1$ to $1$ every $.1$ and apply the formula: $$\texttt{=SQRT(1-RC3^2-R4C^2)}.$$ to get the values of $z$.
We next fill this half-sphere with vertical bars based on the square $[-1,1]\times [-1,1]$: the bases of the bars (pillars) are our little squares in the $xy$-plane and the heights are values of $z$. To see the bars, we simply change the type of the chart plotted by the spreadsheet:
We can see each row of bars as an approximation of the area of a slice of the sphere, which is another circle...
The volume of the sphere is now approximated by the sum of the volumes of the bars. Each of these volumes is the product of
- the height of the bar in this rectangle equal to the value of the function and with the ones outside the domain replaced with $0$s, and
- the area of the base is equal to $.01$.
Their sum is simply the sum of these heights multiplied by $.01$. The result produced by the spreadsheet is the following: $$\text{Approximate volume of the hemisphere}= 2.081.$$ It is close to the theoretical result: $$\text{Exact volume of the hemisphere}= 2\pi/3\approx 2.094.$$ $\square$
Exercise. Approximate the volume of the sphere radius $1$ within $.0001$.
We have showed that indeed the area of a sphere of radius $1$ is close to $A = \frac{4}{3}\pi$. But the real question is: What is the volume? One thing we do know. The volume of a box $a \times b \times c$ is $abc$. With that we can compute volume of various geometric figures with straight edges but what are the volumes of curved objects?
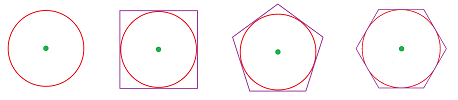
The idea, once again, comes from the ancient Greek's approach to understanding and computing the areas and volumes. They approximated the circle with regular polygons and the sphere with regular polyhedra:
The setup for the Riemann sums for functions of two variables is very similar to the one for numerical functions but by far more cumbersome.
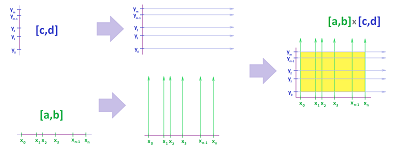
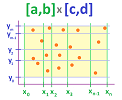
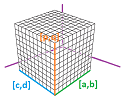
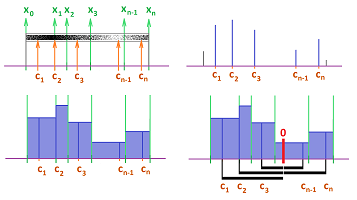
Let's consider a rectangle $R=[a,b]\times [c,d],\ a < b,\ c<d$. Suppose also that we have two integers $n,m \ge 1$. First, we have a partition of $[a,b]$ into $n$ intervals of possibly different lengths: $$ [x_{0},x_{1}],\ [x_{1},x_{2}],\ ... ,\ [x_{n-1},x_{n}],$$ with $x_0=a,\ x_n=b$. The increments of $x$ are: $$\Delta x_i = x_i-x_{i-1},\ i=1,2,...,n.$$ Second, we have a partition of $[c,d]$ into $m$ intervals of possibly different lengths: $$ [y_{0},y_{1}],\ [y_{1},y_{2}],\ ... ,\ [y_{m-1},y_{m}],$$ with $y_0=c,\ y_m=d$. The increments of $y$ are: $$\Delta y_j =y_j-y_{j-1},\ j=1,2,...,m.$$ Altogether, we have a partition $P$ of the rectangle $[a,b]\times [c,d]$ into smaller rectangles $$R_{ij}= [x_{i-1},x_{i}]\times [y_{j-1},y_{j}].$$ These are $2$-cells! The points $$(x_i,y_{j}),\ i=1,2,...,n,\ j=1,2,...,m,$$ will be called the (primary) nodes of the partition.
We are also given the tertiary nodes of $P$ for each pair $i=0,1,2,...,n-1$ and $i,j=0,1,2,...,m-1$:
- a point $U_{ij}$ in the rectangle $R_{ij}=[x_{i-1},x_{i}]\times [y_{j-1},y_{j}]$.
Such a combination of rectangles and tertiary nodes in its intervals will be called an augmented partition $P$ of $R$. We won't need secondary nodes in this chapter.
In the example above, the right upper corners were chosen.
Before we address how to compute volumes, let's consider a simpler problem.
Suppose a function $y = f(X)=f(x,y)$ defined at the tertiary nodes of the partition of the rectangle $R$ and gives us the amount of some material contained in the corresponding cell. Then the total amount of the material in the whole rectangle is simply the sum of the values of $f$.
Definition. The sum of a function $z=f(x,y)$ defined at the tertiary nodes of an augmented partition $P$ of a rectangle $R=[a,b]\times [c,d]$ is defined to be: $$\sum_R f =\sum_{i=1}^n\sum_{j=1}^m f(U_{ij}).$$
Note that when tertiary nodes aren't provided, we can think of the $2$-cells themselves as the inputs of the function: $U_{ij}=R_{ij}= [x_{i-1},x_{i}]\times [y_{j-1},y_{j}]$. This makes $f$ a $2$-form.
The area of each $2$-cell is: $$\Delta A_{ij} = \Delta x_i \cdot \Delta y_j.$$ In other words, the product of the increments of $x$ and $y$ is the increment of the area.
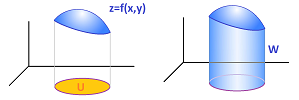
Suppose next we have a function $y = f(X)=f(x,y)$ defined at the tertiary nodes of the partition of the rectangle $R$ and gives us the height of a bar on top of the corresponding cell: $$\text{the volume of }ij\text{ bar} = \underbrace{f(U_{ij})}_{\text{height of bar}} \cdot \overbrace{\Delta x_i}^{\text{depth of base}}\cdot \overbrace{\Delta y_j}^{\text{width of base}}.$$ We then add all of these together in order to compute the volume of the solid under the graph of $z=f(x,y)$ over rectangle $R$.
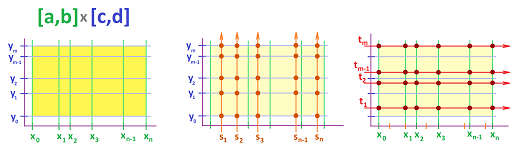
Example. We consider the particular case when the tertiary nodes of $P$ come from the secondary nodes of the augmented partitions of the intervals $[a,b]$ and $[c,d]$: $$U_{ij}=(s_i,t_j).$$
The computation is illustrated below: $$\begin{array}{r|lcccccccr|} &y_0&\Delta y_1&y_1&\Delta y_2&y_3&...&y_{m-1}&\Delta y_m&y_m\\ \hline x_0&\bullet&--&\bullet&--&\bullet&...&\bullet&--&\bullet\\ \Delta x_1&|&f(s_1,t_1)\Delta x_1\Delta y_1&|&f(s_1,t_2)\Delta x_1\Delta y_2&|&...&|&f(s_1,t_m)\Delta x_1\Delta y_m&|\\ x_1&\bullet&--&\bullet&--&\bullet&...&\bullet&--&\bullet\\ \Delta x_2&|&f(s_2,t_1)\Delta x_2\Delta y_1&|&f(s_2,t_2)\Delta x_2\Delta y_2&|&...&|&f(s_2,t_m)\Delta x_2\Delta y_m&|\\ x_2&\bullet&--&\bullet&--&\bullet&...&\bullet&--&\bullet\\ ..&.&..&.&..&.&...&.&..&.\\ x_{n-1}&\bullet&--&\bullet&--&\bullet&...&\bullet&--&\bullet\\ \Delta x_n&|&f(s_n,t_1)\Delta x_n\Delta y_1&|&f(s_n,t_2)\Delta x_n\Delta y_2&|&...&|&f(s_n,t_m)\Delta x_n\Delta y_m&|\\ x_n&\bullet&--&\bullet&--&\bullet&...&\bullet&--&\bullet\\ \hline \end{array}$$ $\square$
Definition. The Riemann sum of a function $z=f(x,y)$ defined at the tertiary nodes of an augmented partition $P$ of a rectangle $R=[a,b]\times [c,d]$ is defined and denoted to be: $$\sum_R f(U_{ij}) \, \Delta x_i\Delta y_j =\sum_{i=1}^n\sum_{j=1}^m f(U_{ij})\Delta x_i\Delta y_j. $$
The Riemann sum of a sampled function of two variables is shown below:
The abbreviated notation for the Riemann sum is: $$\sum_R f \, \Delta x\Delta y . $$
Example. Let's consider a very simple example: $$f(x,y)=x+y, \ R=[0,1]\times [0,1].$$ We choose $$n=2,\ m=2.$$ Then the end-points of the intervals are: $$x_0=0,\ x_1=.5,\ x_2=1 \text{ and }y_0=0,\ y_1=.5,\ y_2=1 .$$ The nodes are $$\begin{array}{ccccccc} (0,1)&-&(.5,1)&-&(1,1)\\ |&&|&&|\\ (0,.5)&-&(.5,.5)&-&(1,.5)\\ |&&|&&|\\ (0,0)&-&(.5,0)&-&(1,0)\\ \end{array}$$ They are the corners of the rectangles of the partition: $$\begin{array}{ccccccc} [0,.5]\times [.5,1]& [.5,1]\times [.5,1]\\ [0,.5]\times [0,.5]& [.5,1]\times [0,.5] \end{array}$$ Now we choose the tertiary nodes. Specifically, let's choose the bottom left corners: $$\begin{array}{|l|l|} \hline (0,.5)& (.5,.5)\\ \hline (0,0)& (.5,0)\\ \hline \end{array} \leadsto \begin{array}{|l|l|} \hline f(0,.5)=.5& f(.5,.5)=1\\ \hline f(0,0)=0& f(.5,0)=.5\\ \hline \end{array}\leadsto \begin{array}{|l|l|} \hline .5\cdot .5^2=.125& 1\cdot .5^2=.25\\ \hline 0\cdot .5^2=0& .5\cdot .5^2=.125\\ \hline \end{array}$$ The values of the function and then the volumes of the bars are shown on right. Then the sum of those is: $$\sum_R f \, \Delta x\Delta y =.5.$$
$\square$
Example. Riemann sums of the paraboloid of revolution:
$\square$
Just as in the one-dimensional case, we are allowed to have negative values of $f$, with possibly negative volumes of the bars. These are the signed distance and the signed volume respectively. We speak then of the volume of the solid between the graph of $z=f(x,y)$ and the rectangle $R$ in the $xy$-plane.
Furthermore, we can have negative lengths for the independent variables too. Suppose $a<b$ and $c<d$, then
- the rectangles $[a,b]\times [c,d]$ and $[b,a]\times [d,c]$ are positively oriented and have positive areas, while
- the rectangles $[a,b]\times [d,c]$ and $[b,a]\times [c,d]$ are negatively oriented and have negative areas.
Once again, the Riemann sum over an oriented rectangle is referred to as the signed volume.
The algebraic properties of sum and Riemann sums are similar to the one in Chapter 11...
Theorem (Constant Function Rule). Suppose $f$ is constant on a rectangle $R$, i.e., $f(x,y) = m$ for all $(x,y)$ in $R$ and some real number $c$. Then $$\sum_R f \, \Delta x\Delta y = m ( b-a )(d-c). $$
Indeed, the Riemann sum represents the area of the rectangle with width $b-a$, the depth $d-c$, and the height $m$.
Properties of the Riemann sums
In spite of their somewhat complex definition, the Riemann sums are finite! There are no issues of infinity or divergence to worry about. They are, therefore, subject to the usual rules of algebra: their terms can be multiplied, factored, re-arranged and added in a different order, etc.
If we proceed to the adjacent rectangle, we can just continue to add terms of the Riemann sum:
Theorem (Additivity Rule). Suppose $z=f(x,y)$ is a function. Suppose $a,b,c,d,q$ are any numbers and suppose we have partitions of the intervals $[a,q]$, $[q,b]$, $[c,d]$ and augmented partitions of the rectangles $[a,q]\times [c,d]$ and $[q,b]\times [c,d]$. Then we have: $$\sum_{[a,q]\times [c,d]} f \, \Delta x\Delta y +\sum_{[q,b]\times [c,d]} f \, \Delta x\Delta y = \sum_{[a,b]\times [c,d]} f \, \Delta x\Delta y,$$ with summations over these partitions.
If two functions are comparable then so are the terms of their Riemann sums:
Theorem (Comparison Rule). Suppose $f$ and $g$ are functions defined on a rectangle $R$. Then we have: $$(1)\ f(x,y)\geq g(x,y) \text{ on } R \ \Longrightarrow\ \sum_R f\, \Delta x\Delta y \geq \sum_R g\, \Delta x\Delta y;$$ $$(2)\ f(x,y)< g(x,y) \text{ on } R \ \Longrightarrow\ \sum_R f\, \Delta x\Delta y < \sum_R g\, \Delta x\Delta y.$$
Theorem (Estimate Rule). Suppose $z=f(x,y)$ is a function. For any $a,b$ with $a<b$ and any $c,d$ with $c<d$, if $$m \leq f(x,y)\leq M,$$ for all $x$ with $a\le x \le b$ and all $y$ with $c\le y\le d$, then $$m(b-a)(d-c)\leq \sum_{[a,b]\times [c,d]} f\, \Delta x\Delta y \leq M(b-a)(d-c).$$
The picture below illustrates the idea of multiplication of the function viz. multiplication of the volume under its graph:
Theorem (Constant Multiple Rule). Suppose $f$ is a function. For any rectangle $R$ and any real $c$, we have: $$ \sum_R (c\cdot f) \, \Delta x\Delta y = c \cdot \sum_R f\, \Delta x\Delta y.$$
The picture below illustrates the idea of adding functions viz. adding the volumes under their graphs:
Theorem (Sum Rule). Suppose $f$ and $g$ are functions. For any rectangle $R$, we have: $$\sum_R \left( f + g \right) \, \Delta x\Delta y = \sum_R f\, \Delta x\Delta y + \sum_R g\, \Delta x\Delta y. $$
Proof. This is a simple algebraic manipulation of the corresponding Riemann sums: $$\begin{array}{lll} \sum_R(f+g) \, \Delta x\Delta y &=\sum_{ij} \left(f(s_i,t_j)+g(s_i,t_j)\right)\Delta A_{ij}\\ &=\sum_{ij} \left(f(s_i,t_j)\Delta A_{ij}+g(s_i,t_j)\Delta A_{ij}\right)\\ &=\sum_{ij}f(s_i,t_j)\Delta A_{ij}+\sum_{ij}g(s_i,t_j)\Delta A_{ij}\\ &=\sum_Rf\, \Delta x\Delta y +\sum_Rg\, \Delta x\Delta y. \end{array}$$ $\blacksquare$
Exercise. Prove the rest of these theorems.
The summation of the Riemann sum can be carried out in two main ways. We can add the rows first and then the resulting column or vice versa. A more profound way is to recognize the presence of functions of single variable in this function of two variables as well as the Riemann sums of these functions in its Riemann sum.
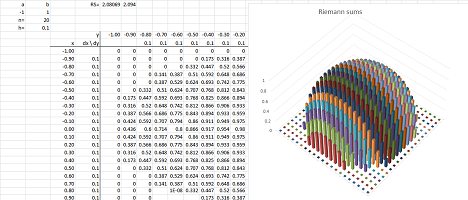
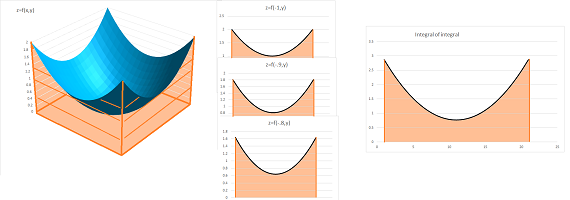
Fixing any value of $x$ creates a new single variable function of $y$ from $z=f(x,y)$: $$f_x(y)=f(x,y).$$ We pick one of the end-points $x=x_i$ of the partition of $[a,b]$ and form the Riemann sum of this function (with respect to $y$ over $[c,d]$): $$\sum_c^d f_{x_i}\, \Delta y =\sum_{j=1}^m f(s_i,t_j)\Delta y_j.$$ For the spreadsheet, the Riemann sum is computed and placed at the cell at its end of each row. As a result the highlighted row of bars in the Riemann sum of the function of two variables, $a$ and $y$, reappears as the Riemann sum of a function of single variable, $y$:
When this is done for each $x_i$, the result is a new function $g$ defined on the end-points of the partition of $[c,d]$: $$g(x_i)=\sum_c^d f_{x_i}\, \Delta y.$$ We now compute its Riemann sum (with respect to $x$ over $[a,b]$): $$\sum_R f\, \Delta x\Delta y =\sum_{i=1}^ng(x_i)\Delta x_i,$$ producing the Riemann sum of the original function $f$. We show this computation for a spreadsheet below:
For the spreadsheet, the Riemann sums placed at the cell at the end of each row, together, produce a column of values, i.e., a function of single variable, $x$. Its Riemann sum is now computed and placed at its bottom. The result is the same (of course!) number as the original, “double” Riemann sum.
Alternatively, for each column, the Riemann sum is computed and placed at the cell at its bottom. Together, the numbers give us a row of values. Its Riemann sum is now computed and placed at its end. The results are the same.
Exercise. Carry out the missing part of the above analysis starting with: “Fixing any value of $y$ creates a new single variable function of $x$ from $z=f(x,y)$...”.
Our analysis amounts to the following formula.
Theorem (Riemann sum of Riemann sums). $$\begin{array}{lll} \sum_R f \, \Delta x\Delta y &=\sum_{i=1}^n\left(\sum_{j=1}^m f(s_i,t_j)\Delta y_j\right)\Delta x_i\\ &=\sum_{j=1}^m\left(\sum_{i=1}^n f(s_i,t_j)\Delta x_i\right)\Delta y_j. \end{array}$$
In other words, the order of summation doesn't matter.
The Riemann integral over rectangles
The familiar integral of a numerical function is the (algebraic) area under the graph and now this is the volume under the graph of a function of two variables. It is as if we used to look at a certain sandbox from aside and tried to find the area of the visible sand as a way to determine the amount of sand in it and now we stand up and see that this was just a cross-section and we need to start to think three-dimensional...
Recall that the function is defined on the rectangle partitioned into smaller rectangles and then it is sampled -- in a possibly non-uniform manner -- in each. The locations are called the secondary nodes. The result is a two-dimensional array of numbers: $$\text{heights: }\begin{array}{|cccccc} \hline \ f(s_1,t_1)&f(s_1,t_2)&...\\ \ f(s_2,t_1)&f(s_2,t_2)&...\\ ...&...&... \end{array}\quad\leadsto\quad \text{volumes: } \begin{array}{|cccccc} \hline \ f(s_1,t_1)\Delta A_{11}&f(s_1,t_2)\Delta A_{12}&...\\ \ f(s_2,t_1)\Delta A_{21}&f(s_2,t_2)\Delta A_{22}&...\\ ...&...&... \end{array}$$ The sum of all the members of this array is the Riemann sum of the function.
Now, the Riemann sums are just approximations of the volume and in order to improve them, we have to refine the partition. And we keep refining, so that we have simultaneously: $$n,m \to \infty \text{ and } \Delta x_i, \Delta y_j\to 0.$$
To make this idea specific, we define the mesh of a partition $P$ as: $$|P|=\max_{i,j} \, \{ \Delta x_i,\ \Delta y_j\}.$$ It is a measure of “refinement” of $P$.
Definition. The Riemann integral of a function $z=f(x,y)$ over rectangle $R=[a,b]\times [c,d]$ is defined to be the limit of a sequence of its Riemann sums with the mesh of their augmented partitions $P_k$ approaching $0$ as $k\to \infty$. When all these limits exist and are all equal to each other, $f$ is called an integrable function over $R$ and the result is denoted by: $$ \iint_R f(x,y)\, dxdy =\lim_{k \to \infty} \sum_R f_k \, \Delta x\Delta y,$$ where $f_k$ is $f$ sampled at the secondary nodes of the partition. It is also called the definite integral, the double integral, or simply integral, of $f$ over $R$ called the domain of integration. When all these limits are equal to $+\infty$ (or $-\infty$), we say that the integral is infinite and write: $$ \iint_R f(x,y)\, dxdy =+\infty\ (\text{or }-\infty).$$
An abbreviated notation is: $$\iint_R f\, dA ,$$ where “$A$” stands for “area”.
We will also refer to the integral as well as the (signed) volume under the graph of $f$ or the (signed) volume between the graph and the $xy$-plane.
The custom of placing the domain of integration under the integral sign is also applied to the numerical functions, as follows: $$\int_a^bf\, dx=\int_{[a,b]}f\, dx.$$ Instead of “from $a$ to $b$” we have now an integral “over $[a,b]$”. The advantage of the old notation is that it specifies the orientation of the segment $[a,b]$. From now on, all orientations are positive by default.
In general, we follow the rule: $$\text{orientation of }[a,b] = \operatorname{sign}(b-a),$$ and $$\text{orientation of }[a,b]\times [c,d]\ = \operatorname{sign}((b-a)(d-c)).$$
Let's verify the definition for a simple function.
Theorem (Constant Integral Rule). Suppose $z=f(x,y)$ is constant on rectangle $R=[a,b]\times [c,d]$, i.e., $f(x,y) = m$ for all $(x,y)$ in $R$ and some real number $m$. Then $f$ is integrable on $R$ and $$\iint_R f\, dA = m (b-a)(d-c).$$
The following result proves that our definition makes sense for a large class of functions.
Theorem. All continuous functions on rectangle $R$ are integrable on $R$.
Proof. $\blacksquare$
The converse isn't true because the sign function $\operatorname{sign}(xy)$ is integrable over any rectangle.
We once again utilize the idea of signed distance, signed area, and signed volume.
Theorem (Orientation). The Riemann integral of a function $z=f(x,y)$ over rectangle $[b,a]\times [c,d]$ is equal to the negative of the integral over $[a,b]\times [c,d]$: $$\iint_{[b,a]\times [c,d]} f\, dA =-\iint_{[a,b]\times [c,d]} f\, dA ;$$ and, similarly, $$\iint_{[a,b]\times [d,c]} f\, dA =-\iint_{[a,b]\times [c,d]} f\, dA ;$$ but $$\iint_{[b,a]\times [d,c]} f\, dA =\iint_{[a,b]\times [c,d]} f\, dA .$$
It all depends on whether the rectangle is positively or negatively oriented!
Now the properties of the Riemann integral. The mimic the ones for numerical functions but they follow from the corresponding properties of the Riemann sums (and the analogous rules of limits).
The additivity property for integrals -- combining the domains of integration -- of numerical functions, $$\int_a^b f(x)\, dx +\int_a^b f(x)\, dx = \int_a^b f(x)\, dx,$$ has a match. The interpretation is the same: the amount of a quantity contained in a region formed by two regions with a negligible overlap is equal to the sum of the quantities in the two. We just look at the region from above which reveals the third dimension. So, we switch from areas to volumes:
It's as if we put a divider in our sandbox... The result follows from the Additivity for Riemann sums.
Theorem (Additivity). Suppose a function $z=f(x,y)$ is integrable over the rectangles $$R=[a,q]\times [c,d] \text{ and }S=[q,b]\times [c,d].$$ Then $f$ is integrable over the rectangle $R\cup S=[a,b]\times [c,d]$ and we have: $$\iint_R f\, dA +\iint_S f\, dA = \iint_{R\cup S} f\, dA .$$
Thus, adding the domains of integration adds the integrals too.
Theorem. If $z=f(x,y)$ is integrable over $R$ then it is also integrable over any rectangle $R'$ in $R$.
The following is another important corollary.
Theorem. All piece-wise continuous functions are integrable.
Proof. It follows from the integrability of continuous functions and the Additivity Rule. $\blacksquare$
In particular, all step-functions are integrable...
Just as before, the larger function contains a larger volume under its graph:
Theorem (Comparison Rule). If $$f(x,y)\geq g(x,y) \text{ for all }(x,y)\text{ in rectangle } R,$$ then $$\iint_R f\, dA \geq \iint_R g\, dA ,$$ provided $z=f(x,y)$ and $z=g(x,y)$ are integrable functions over $R$. Otherwise we have: $$\begin{array}{lll} \iint_R f\, dA =-\infty&\Longrightarrow& \iint_R g\, dA =-\infty;\\ \iint_R f\, dA =+\infty&\Longleftarrow& \iint_R g\, dA =+\infty. \end{array}$$
If we know only estimates of the function, we have an estimate -- below and above -- for the volume under its graph.
For the general case, we have the following.
Theorem (Estimate Rule). Suppose $z=f(x,y)$ is an integrable function over $R=[a,b]\times [c,d]$. Then, if $a<b$ and $c<d$ and $$m \leq f(x,y)\leq M,$$ for all $(x,y)$ in $R$, we have $$m (b-a)(d-c)\leq \iint_R f\, dA \leq M (b-a)(d-c).$$
Exercise. What if the orientation of the rectangle is negative?
Finally, these are the algebraic properties. First, the picture below illustrates the idea that tripling the height of a surface will need tripling the amount of soil under it:
Theorem (Constant Multiple Rule). Suppose $z=f(x,y)$ is an integrable function over a rectangle $R$. Then so is $c\cdot f$ for any real $c$ and we have: $$ \iint_R(c\cdot f)\, dA = c \cdot \iint_R f\, dA.$$
Finally, the picture below illustrates what happens when the bottom drops from a bucket of sand and it falls on a curved surface:
Theorem (Sum Rule). Suppose $z=f(x,y)$ and $z=g(x,y)$ are integrable functions over a rectangle $R$. Then so is $f+g$ and we have: $$\iint_R \left( f + g \right)\, dA = \iint_R f\, dA + \iint_R g\, dA.$$
Proof. We take the limit, as $|P|\to 0$, of the Sum Rule for Riemann sums: $$\begin{array}{cccc} \sum_R(f+g) \, \Delta x\Delta y &=&\sum_Rf\, \Delta x\Delta y &+&\sum_Rg\, \Delta x\Delta y \\ \downarrow&&\downarrow&&\downarrow\\ \iint_R (f + g)\, dA&&\iint_R f\, dA&&\iint_R g\, dA. \end{array}$$ The transition is justified by the Sum Rule for Limits. $\blacksquare$
Exercise. Prove the rest of these theorems.
The actual computations of integrals require single integrals. The method is derived from the Riemann sum of Riemann sums formula in the last section.
We recognize the presence of functions of single variable in this function of two variables as well as the Riemann sums and the integrals of these functions in its Riemann sum and the integral.
Fixing any value of $x$ creates a new single variable function of $y$ from $z=f(x,y)$: $$f_x(y)=f(x,y).$$ We pick one and form the Riemann integral of this function: $$\int_c^df_{x}\, dy=\int_{y=c}^{y=d} f(x,y)\, dy.$$ This integral is with respect to $y$ with the domain of integration $[c,d]$. It represents the area of the cross section of our solid!
When this is done for each $x$, the result is a new function $g$ defined on the interval $[a,b]$: $$g(x)=\int_c^d f_{x}\, dy.$$ We now compute its Riemann integral: $$\int_R f\, dxdy=\int_{a}^b g\, dx,$$ This integral is with respect to $x$ with the domain of integration $[a,b]$. It produces the Riemann integral of the original function $z=f(x,y)$.
Alternatively, for each $y$, the Riemann integral is computed and, together, these numbers form a function of $y$. Its Riemann integral is now computed. The results are the same.
Exercise. Carry out the missing part of the above analysis starting with: “Fixing any value of $y$ creates a new single variable function of $x$ from $z=f(x,y)$...”.
Our analysis amounts to the following formula similar to the formula for the second, mixed partial derivative.
Theorem (Fubini's Theorem: integral of integral). If a function $z=f(x,y)$ is integrable over a rectangle $R=[a,b]\times [c,d]$, then it is also integrable with respect to $x$ over the interval $[a,b]$ and with respect to $y$ over the interval $[c,d]$; moreover, we have: $$\begin{array}{lll} \iint_R f\, dA&=\int_{x=a}^{x=b}\left(\int_{y=c}^{y=d} f(x,y)\, dy \right)\, dx\\ &=\int_{y=c}^{c=d}\left(\int_{x=a}^{x=b} f(x,y)\, dx \right)\, dy. \end{array}$$
Proof. $\blacksquare$
The right-hand sides are called iterated integrals. They supply as, for the first time, with a method for computing area integrals!
The method relies on an approach similar to partial differentiation in that we initially treat $y$ as the only variable and, then, $x$ has to be treated as a constant. This coordinate-by-coordinate integration may be called “partial integration”.
Example. Fubini's Theorem allows us to use the Fundamental Theorem of Calculus: $$\begin{array}{lll} \iint_{[0,1]\times [0,2]} xy\, dxdy&=\int_{x=0}^{x=1}\left(\int_{y=0}^{y=2} xy\, dy \right)\, dx&\text{use the CMR...}\\ &=\int_{x=0}^{x=1}x\left(\int_{y=0}^{y=2} y\, dy \right)\, dx&\text{use the FTC...}\\ &=\int_{x=0}^{x=1}x\left(\frac{y^2}{2}\bigg|_{y=0}^{y=2} \right)\, dx\\ &=\int_{x=0}^{x=1}x\left(2 \right)\, dx&y\text{ is gone!}\\ &=2\int_{x=0}^{x=1}x\, dx&\text{use the FTC...}\\ &=2\frac{x^2}{2}\bigg|_{x=0}^{x=1}\\ &=1. \end{array}$$ $\square$
Using “$x=,\ y=$” is optional and so are the parentheses: $$\iint_{[0,1]\times [0,2]} xy\, dxdy=\int_{0}^{1}\int_{0}^{2} xy\, dydx.$$
Non-rectangular domains of integration, such as the disk, are still to come.
The weight as the 3d Riemann sum
We can find volumes of various objects and, therefore, their weights -- as long as the density is constant! What if the density is variable? We don't have a solution. Even simpler, what is the mass of a rectangular contained (box) filled with a gas of variables density?
Recall the two main metaphors (in addition to that of motion) we have used for integrals: $$\begin{array}{lllll} \text{variables}&\text{domain}&\text{metaphor #1}&\text{metaphor #2}\\ \hline 1&\text{interval }[a,b]&\text{area under the graph in }{\bf R}^2&\text{linear density}\\ 2&\text{rectangle }[a,b]\times [c,d]&\text{volume under the graph in }{\bf R}^3&\text{planar density}\\ 3&\text{box }[a,b]\times [c,d]\times [p,q]&\text{volume? under? the graph in }{\bf R}^4?&\text{density} \end{array}$$ It is hard to provide a similar interpretation for the $3$ variables. As we have run out of dimensions to visualize these functions, we choose the second metaphor: a function of three variables $u=f(x,y,z)$ is understood as the density of the medium at location $(x,y,z)$. The level surfaces below show where the density is the same.
In addition to the common meaning of density, i.e., the distribution of weight, we can speak of the density of a particular material within the medium, the density of population, the temperature (the density of heat), etc.
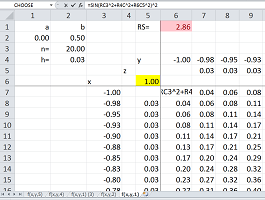
Example. Spreadsheets are tables of numbers and may only be good for representing functions of up to two variables, $x$ and $y$. To add the third, $z$, we use “sheets”, one for each value of $z$:
We enter the value of $z$ at the corner of our table of values of $f$. The formula in each cell of this table refers -- just as before -- to the values of $x$ (the first column) and $y$ (the top row) as well as this single entry for $z$: $$\texttt{=SIN(RC3^2+R4C^2+R6C5^2)^2}.$$ A few more sheets, or layers, are created with different entries for $z=1,2,3,4,5$. The result is a box, or a three-dimensional array, of numbers.
The graphs shown are those of the functions of two variables: $u=f(x,y,1),u=f(x,y,2)$, etc.
The graph of each of these functions can again be seen to represent a terrain. Now, what if we think of $z$ as time? Then we face a terrain changing in time! Such a process could be a wave (the sea, a drum, etc.). $\square$
The function is represented by a list of rectangular arrays. Alternatively, we see it as a rectangular array of lists...
The setup for the Riemann sums for functions of three variables is very similar to the one for two.
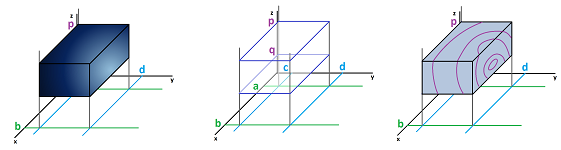
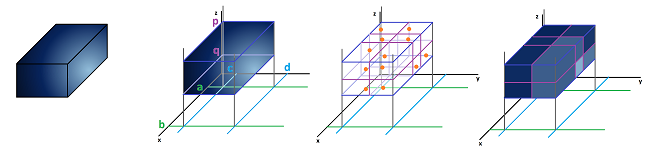
Suppose we have a function $u = f(x,y,z)$ defined on a box $$B=[a,b]\times [c,d]\times [p,q],\ a < b,\ c<d,\ p<q.$$ Suppose also that we have two integers $n,m,r \ge 1$. We have three partitions of these intervals: $$\begin{array}{lllll} \text{axis}&\text{segment}&\text{end-points}&\text{lengths}\\ \hline x&[a,b]& a=x_{0}<x_{1}<x_{2}< ... < x_{n-1}<x_n=b&\Delta x_i =x_i-x_{i-1}\\ y&[c,d]& c=y_{0}<y_{1}<y_{2}< ... < y_{m-1}<y_m=d&\Delta y_j =y_j-y_{j-1}\\ z&[p,q]& p=z_{0}<z_{1}<z_{2}< ... < z_{n-1}<z_r=q&\Delta z_k =z_k-z_{k-1} \end{array}$$ Altogether, we have a partition $P$ of the box $B$ into smaller boxes or compartments: $$B_{ijk}= [x_{i},x_{i+1}]\times [y_{j},y_{j+1}]\times [z_{k},z_{k+1}].$$ We know these boxes as $3$-cells. The whole partition may look like this wire-frame (it is non-uniform in general):
The volume of each $3$-cell is: $$\Delta V_{ijk} = \Delta x_i \cdot \Delta y_j\cdot \Delta z_k.$$ In other words, the product of the increments of $x$, $y$, and $z$ is the increment of the volume.
The points $$X_{ijk}=(x_i,y_{j},z_k),\ i=1,2,...,n,\ j=1,2,...,m,\ k=1,2,...,r,$$ are the primary nodes, or the nodes of degree $0$. What about the secondary, etc. nodes? We have a more uniform look at the nodes consistent with our view on cells. These are the $3$-cells of our partition as well as the lower-dimensional cells that make up the boundaries of these cells: $$\begin{array}{lll} \text{ cells }&\text{ terms }&\text{ product representation }&\text{ nodes }&\text{ }\\ \hline 3\text{-cells}&\text{ boxes }&[x_{i},x_{i+1}]\times [y_{j},y_{j+1}]\times [z_{k},z_{k+1}]&\\ 2\text{-cells}&\text{ faces }&[x_{i},x_{i+1}]\times [y_{j},y_{j+1}]\times \{z_{k}\}&\text{ tertiary nodes}\\ &&[x_{i},x_{i+1}]\times \{y_{j}\}\times [z_{k},z_{k+1}]\\ &&\{x_{i}\}\times [y_{j},y_{j+1}]\times [z_{k},z_{k+1}]\\ 1\text{-cells}&\text{ edges }&[x_{i},x_{i+1}]\times \{y_{j}\}\times \{z_{k}\}&\text{ secondary nodes}\\ &&\{x_{i}\}\times [y_{j},y_{j+1}]\times \{z_{k}\}\\ &&\{x_{i}\}\times \{y_{j}\}\times [z_{k},z_{k+1}]\\ 0\text{-cells}&\text{ vertices }&\{x_{i}\}\times \{y_{j}\}\times \{z_{k}\}&\text{ primary nodes}\\ \end{array}$$
For the weight we will only need the nodes at the $3$-cells; for each triple $i=0,1,2,...,n-1$, $j=0,1,2,...,m-1$, and $k=0,1,2,...,r-1$, we have:
- a point $S_{ijk}$ in the box $B_{ijk}$.
Such a combination of boxes and nodes will be called an augmented partition of $B$.
Before we address how to compute the weight, let's consider a simpler problem.
Suppose a function $y = f(X)=f(x,y,z)$ defined at $S_{ijk}$ and gives us the amount of some material contained in the corresponding compartment. Then the total amount of the material in the whole box is simply the sum of the values of $f$.
Definition. The sum of a function $z=f(x,y)$ defined at the nodes at the $3$-cells of an augmented partition $P$ of a box $R=[a,b]\times [c,d]\times [p,q]$ is defined to be: $$\sum_B f=\sum_{i=1}^n\sum_{j=1}^m \sum_{k=1}^r f(S_{ijk}).$$
Note that when these nodes aren't provided, we can think of the $3$-cells themselves as the inputs of the function: $S_{ijk}=B_{ijk}$. This makes $f$ a $3$-form.
Each degree $3$ node gives us the density (as if constant) of the medium in the corresponding box: $$\text{the weight of box }B_{ijk} = \underbrace{f(S_{ijk})}_{\text{density}} \cdot \overbrace{\Delta x}^{\text{depth of box}}\cdot \overbrace{\Delta y}^{\text{width of box}}\cdot \overbrace{\Delta y}^{\text{height of box}}. $$ We then add all of these together in order to approximate the weight of the solid in the box of $u=f(x,y,z)$ inside box $B$. For each $k$, the values in the $k$th layer look like this: $$\begin{array}{r|lcccccc} z_k&y_0&\Delta y_1&y_1&\Delta y_2&y_2&...\\ \hline x_0&\bullet&--&\bullet&--&\bullet&...\\ \Delta x_1&|&f(S_{1,1,k})\Delta x_1\Delta y_1\Delta z_k&|&f(S_{1,2,k})\Delta x_1\Delta y_2\Delta z_k&|&...\\ x_1&\bullet&--&\bullet&--&\bullet&...\\ \Delta x_2&|&f(S_{2,1,k})\Delta x_2\Delta y_1\Delta z_k&|&f(S_{2,2,k})\Delta x_2\Delta y_2\Delta z_k&|&...\\ x_2&\bullet&--&\bullet&--&\bullet&...\\ ..&.&..&.&..&.&...&.&..&.\\ \end{array}$$
Definition. The Riemann sum of a function $u=f(x,y,z)$ defined at the nodes at the $3$-cells of an augmented partition $P$ of a box $B=[a,b]\times [c,d]\times [p,q]$ is defined to be $$\sum_B f\, \Delta x\Delta y\Delta z =\sum_{i=1}^n\sum_{j=1}^m\sum_{k=1}^r f(S_{ijk})\Delta x_i\Delta y_j\Delta z_k. $$
The abbreviated formula is: $$\sum_B f\, \Delta x\Delta y \Delta z=\sum_{i,j,k} f(S_{ijk})\Delta V_{ijk} $$
Just as before, we are allowed to have negative values of $f$. Furthermore, we can have negative lengths of the intervals for the independent variables. The box $[a,b]\times [c,d]\times [p,q]$ has a positive orientation whenever $a<b,\ c<d,\ p<q$; in other words, when all three segments have positive orientations within their respective axes. A reversal of the orientation of a single segment reverses the orientation of the box.
Exercise. What if the orientations of two segments are reversed?
The weight as the 3d Riemann integral
Now, if the density function varies continuously, the Riemann sums are just approximations of the actual weight and, in order to improve them, we have to refine the partition: $$n,m,r \to \infty \text{ and } \Delta x_i, \Delta y_j, \Delta z_k\to 0.$$ Just as before, we define the mesh of a partition $P$ as: $$|P|=\max_{i,j,k} \, \{ \Delta x_i,\ \Delta y_j, \Delta z_k\}.$$ It is a measure of “refinement” of $P$.
Definition. The Riemann integral of a function $u=f(x,y,z)$ over box $B=[a,b]\times [c,d]\times [p,q]$ is defined to be the limit of a sequence of its Riemann sums with the mesh of their augmented partitions $P_s$ approaching $0$ as $s\to \infty$. When all these limits exist and are all equal to each other, $f$ is called an integrable function over $B$ and the result is denoted by: $$ \iiint_B f(x,y,z)\, dxdydz =\lim_{s \to \infty} \sum_B f_s\, \Delta x\Delta y\Delta z,$$ where $f_s$ is $f$ sampled over the partition $P_s$. It is also called the definite integral, the triple integral, or simply integral, of $f$ over $B$. When all these limits are equal to $+\infty$ (or $-\infty$), we say that the integral is infinite and write: $$ \iiint_R f(x,y,z)\, dxdydz =+\infty\ (\text{or }-\infty).$$
An abbreviated notation is: $$\iiint_B f\, dV .$$
Theorem (Constant Integral Rule). Suppose $z=f(x,y,z)$ is constant on box $B=[a,b]\times [c,d]\times [p,q]$, i.e., $f(x,y,z) = m$ for all $(x,y,z)$ in $B$ for some real number $m$. Then $f$ is integrable over $B$ and $$\iiint_B f\, dV = m (b-a)(d-c)(q-p).$$
Theorem. All continuous functions on box $B$ are integrable on $B$.
Proof. $\blacksquare$
The converse isn't true...
The properties of the Riemann integral mimic the ones for numerical functions (and functions of two variables).
The interpretation of additivity is the same: the quantity in a region formed from two regions with a negligible overlap is equal to the sum of the quantities in the two.
It's as if we put a divider in our container...
Theorem (Additivity). Suppose a function $u=f(x,y,z)$ is integrable over the boxes $$R=[a,q]\times [c,d]\times [p,q] \text{ and }S=[q,b]\times [c,d]\times [p,q].$$ Then $f$ is integrable over the box $R\cup S=[a,b]\times [c,d]\times [p,q]$ and we have: $$\iiint_R f\, dV +\iiint_S f\, dV = \iiint_{R\cup S} f\, dV .$$
Thus, adding the domains of integration adds the integrals too.
Theorem. If $u=f(x,y,z)$ is integrable over box $B$ then it is also integrable over any box $B'$ in $B$.
Theorem. All piece-wise continuous functions are integrable.
Just as before, the box with a larger density weighs more:
Theorem (Comparison Rule). If $$f(x,y,z)\geq f(x,y,z) \text{ for all }(x,y,z)\text{ in box } B,$$ then $$\iiint_B f\, dV \geq \iiint_B f\, dV ,$$ provided $z=f(x,y,z)$ and $z=g(x,y,z)$ are integrable functions over $B$. Otherwise we have: $$\begin{array}{lll} \iiint_B f\, dV =-\infty&\Longrightarrow& \iiint_B g\, dV =-\infty;\\ \iiint_B f\, dV =+\infty&\Longleftarrow& \iiint_B g\, dV =+\infty. \end{array}$$
If we know only estimates of the density, we have an estimate -- below and above -- for the weight of the box.
Theorem (Estimate Rule). Suppose $u=f(x,y,z)$ is an integrable function over box $B=[a,b]\times [c,d]\times [p,q]$. Then, if $a<b$, $c<d$, $p<q$, and $$m \leq f(x,y,z)\leq M,$$ for all $(x,y,z)$ in $B$, we have $$m (b-a)(d-c)(q-p)\leq \iiint_R f\, dV \leq M (b-a)(d-c)(q-p).$$
Exercise. What if the orientation of the box is negative?
Finally, these are the algebraic properties. First, the picture below illustrates the idea that tripling the density of a solid will triple its weight:
Theorem (Constant Multiple Rule). Suppose $u=f(x,y,z)$ is an integrable function over a box $B$. Then so is $c\cdot f$ for any real $c$ and we have: $$ \iiint_B(c\cdot f)\, dV = c \cdot \iiint_B f\, dV.$$
Second, the picture below illustrates that when gas is pumped from one container to another that already contains gas, the resulting density is the sum of the two:
Theorem (Sum Rule). Suppose $u=f(x,y,z)$ and $u=g(x,y,z)$ are integrable functions over a box $B$. Then so is $f+g$ and we have: $$\iiint_B \left( f + g \right)\, dV = \iiint_B f\, dV + \iiint_B g\, dV.$$
Exercise. Prove these theorems.
The actual computations of integrals require single integrals. We recognize the presence of functions of single variable in this function of three variables as well as the Riemann sums and the integrals of these functions in its Riemann sum and the integral.
Theorem (Fubini's Theorem: integral of integral of integral). If a function $u=f(x,y,z)$ is integrable over a box $B=[a,b]\times [c,d]\times [p,q]$, then it is also integrable with respect to $x$ over the interval $[a,b]$, with respect to $y$ over the interval $[c,d]$, and with respect to $z$ over the interval $[p,q]$; moreover, we have (in any order of variables): $$\iiint_B f\, dV=\int_{x=a}^{x=b}\left(\int_{y=c}^{y=d} \left(\int_{z=p}^{z=q} f(x,y,z)\, dz \right)\, dy \right)\, dx.$$
Example. We gradually progress from inside out: $$\begin{array}{lll} \iiint_{[0,1]\times [0,2]\times [0,3]} x^3y^2z\, dV &=\int_{x=0}^{x=1}\left(\int_{y=0}^{y=2} \left(\int_{z=0}^{z=3} x^3y^2z\, dz \right)\, dy \right)\, dx\\ &=\int_{x=0}^{x=1}\left(\int_{y=0}^{y=2} x^3y^2\left(\int_{z=0}^{z=3} z\, dz \right)\, dy \right)\, dx\\ &=\int_{x=0}^{x=1}\left(\int_{y=0}^{y=2} x^3y^2\left( \frac{z^2}{2}\bigg|_{z=0}^{z=3} \right)\, dy \right)\, dx\\ &=\int_{x=0}^{x=1}\left(\int_{y=0}^{y=2} x^3y^2\left( \frac{9}{2} \right)\, dy \right)\, dx&z\text{ is gone!}\\ &=\int_{x=0}^{x=1}\frac{9}{2}x^3\left(\int_{y=0}^{y=2} y^2\, dy \right)\, dx\\ &=\int_{x=0}^{x=1}\frac{9}{2}x^3\left( \frac{y^3}{3}\bigg|_{y=0}^{y=2} \right)\, dx\\ &=\int_{x=0}^{x=1}\frac{9}{2}x^3\left( \frac{8}{3} \right)\, dx&y\text{ is gone!}\\ &= 12\int_{x=0}^{x=1}x^3\, dx\\ &= 12\frac{x^4}{4}\bigg|_{x=0}^{x=1}\\ &=12\frac{1}{4}&x\text{ is gone too!}\\ &=3. \end{array}$$ $\square$
Specifying the variables of the bounds of integration as well as using the parentheses is optional.
Example. Alternative notation: $$\begin{array}{lll} \iiint_{[0,1]\times [0,2]\times [0,3]} x^3y^2z\, dV &=\int_{ 0}^{ 1}&\int_{ 0}^{ 2} &\int_{ 0}^{ 3} x^3y^2z\, dz & \, dy & \, dx\\ &=\int_{ 0}^{ 1}&\int_{ 0}^{ 2} x^3y^2&\int_{ 0}^{ 3} z\, dz & \, dy & \, dx\\ &=\int_{ 0}^{ 1}&\int_{ 0}^{ 2} x^3y^2& \frac{z^2}{2}\bigg|_{ 0}^{ 3} & \, dy & \, dx\\ &=\int_{ 0}^{ 1}&\int_{ 0}^{ 2} x^3y^2& \frac{9}{2} & \, dy & \, dx\\ &=\int_{ 0}^{ 1}\frac{9}{2}x^3&\int_{ 0}^{ 2} &y^2&\, dy & \, dx\\ &=\int_{ 0}^{ 1}\frac{9}{2}x^3&& \frac{y^3}{3}\bigg|_{ 0}^{ 2} && \, dx\\ &=\int_{ 0}^{ 1}\frac{9}{2}x^3&& \frac{8}{3} && \, dx\\ &= 12\int_{ 0}^{ 1}x^3\, dx\\ &= 12\frac{x^4}{4}\bigg|_{ 0}^{ 1}\\ &=12\frac{1}{4}\\ &=3. \end{array}$$ $\square$
Non-rectangular domains, such as the ball, are still to come.
Lengths, areas, volumes, and beyond
What do the types of Riemann sums and integrals that we have considered have in common?
Example. Suppose we would like to find the average height of a building in a city. For simplicity, we assume that there is one building in each block. The city might look like this:
For our computations we collect the heights of these building and put them in a table, which makes a function of two variables $f$. These may be its inputs and outputs: $$\begin{array}{l|cccc} y\backslash x&0&1&2&...&10\\ \hline 0&(0,0)&(0,1)&(0,2)&...&(0,10)\\ 1&(1,0)&(1,1)&(2,2)&...&(1,10)\\ 2&(2,0)&(1,1)&(2,2)&...&(2,10)\\ ...&...&...&...&...\\ 10&(10,0)&(10,1)&(10,2)&...&(10,10)\\ \end{array}\quad\leadsto\quad \begin{array}{l|cccc} y\backslash x&0&1&2&...&10\\ \hline 0&1&3&5&...&0\\ 1&2&4&6&...&0\\ 2&3&5&7&...&1\\ ...&...&...&...&...\\ 10&0&1&7&...&0\\ \end{array}$$ This may look like a generic function of two variables $z=f(x,y)$, but let's take a closer look at how the data. It's not a single number for each location but for each block, i.e., a rectangle. The data then is represented by a table: $$\begin{array}{l|cccc} y\backslash x&0&&1&&2&&3&...&9&&10\\ \hline 0&\bullet&--&\bullet&--&\bullet&--&\bullet&...&\bullet&--&\bullet\\ &|&1&|&3&|&5&|&...&|&0&|\\ 1&\bullet&--&\bullet&--&\bullet&--&\bullet&...&\bullet&--&\bullet\\ &|&2&|&4&|&6&|&...&|&0&|\\ 2&\bullet&--&\bullet&--&\bullet&--&\bullet&...&\bullet&--&\bullet\\ &|&3&|&5&|&7&|&...&|&1&|\\ 3&\bullet&--&\bullet&--&\bullet&--&\bullet&...&\bullet&--&\bullet\\ ...&&...&&...&&...&&...&&...\\ 9&\bullet&--&\bullet&--&\bullet&--&\bullet&...&\bullet&--&\bullet\\ &|&0&|&1&|&7&|&...&|&0&|\\ 10&\bullet&--&\bullet&--&\bullet&--&\bullet&...&\bullet&--&\bullet\\ \end{array}$$ We realize that this isn't just a function of two variables; it's a discrete $2$-form! Then to find the average height, we find the total of the heights of the buildings, which is the sum of $f$ over the rectangle $R=[0,10]\times [0,10]$: $$\text{total height }= \sum_{R}f,$$ and then divide by the number of buildings: $$\text{average height }= \frac{1}{10\cdot 10}\sum_{R}f.$$ However, a more complex situation is that of a city with blocks of various dimensions. In that case, the average height is the total of the volumes of the buildings, which is the Riemann sum of the heights over $R$: $$\text{total volume }= \sum_{ij}f(X_{ij})\, \Delta A_{ij}=\sum_{R}f \, \Delta x\Delta y,$$ divided by the area of the city, $100$: $$\text{average height }= \frac{1}{\text{area of }R}\sum_{R}f\, \Delta x\Delta y.$$ $\square$
The analysis applies to the idea of the average amount of any material spread over a region.
Some are familiar for the three cases of dimensions $1,2,3$: $$\begin{array}{llll} \text{average density of segment }I&=\frac{1}{\text{length of }I}\sum_I f\, \Delta x,\\ \text{average density of rectangle }R&=\frac{1}{\text{area of }R}\sum_R f\, \Delta x\Delta y,\\ \text{average density of box }B&=\frac{1}{\text{volume of }B}\sum_B f\, \Delta x\Delta y\, \Delta z.\\ \end{array}$$ Here, the meaning varies: $$\begin{array}{lllll} \dim&\text{domain}&\text{space}&\text{measure}&f \text{ is...}&\sum_Uf \, \Delta x... \text{ is...}\\ \hline 1&\text{interval }&\text{ in }{\bf R}^1&\text{length}&\text{linear density}&\text{total amount}\\ 2&\text{rectangle }&\text{ in }{\bf R}^2&\text{area}&\text{planar density}&\text{total amount}\\ 3&\text{box }&\text{ in }{\bf R}^3&\text{volume}&\text{density}&\text{total amount}\\ ...\\ \end{array}$$
Do we continue?
To proceed to the $n$-dimensional case, we first need to understand how to measure the size of this $n$-dimensional “box”. Recall that an $n$-cell in ${\bf R}^n$ is the set of all points each coordinate of which lies within a predetermined interval of values. In other words, for any list of $n$ pairs of real numbers, $$a_1<b_1,\ a_2<b_2,\ ...,\ a_n<b_n,$$ we define the box to be $$B=\{X=(x_1,x_2,...,x_n):\ a_i \le x_i \le b_i,\ i=1,2,...,n\}.$$ The notation we have used is: $$B=[a_1,b_1]\times[a_2,b_2]\times...\times [a_n,b_n].$$ The $n$-volume of the box $B$ is simply the product of the lengths of the intervals that make it up: $$v(B)=(b_1-a_1)(b_2-a_2)...(b_n-a_n).$$ Now, the faces of this $n$-box are $(n-1)$-cells.
Together they form the boundary of the $n$-cell.
It is important that the $n$-volume of an $(n-1)$-cell is zero! That is why we can create a partition of an $n$-cell into smaller $n$-cell as long as they only intersect by their faces.
This is the $n$th row in the table above: $$\begin{array}{lllll} \dim&\text{domain}&\text{space}&\text{measure}&f \text{ is...}&\sum_Bf\, \Delta V \text{ is...}\\ \hline n&\text{cell }&\text{ in }{\bf R}^n&n\text{-volume}&\text{density}&\text{total amount} \end{array}$$
Now, what is the meaning of the Riemann sum $\sum_Bf\, \Delta V $?
The $n$-cell $B$ is the product of the intervals located in the axes of ${\bf R}^n$. We provide a partition for each. These partitions cut $B$ into smaller $n$-cells creating a partition $P$. A discrete $n$-form $f$ is then a function that assigns a number to each of these cells.
Definition. The Riemann sum of a discrete $n$-form $f$ over a partition of an $n$-cell $B$ is defined to be: $$\sum_B f\, \Delta V=\sum_C f(C)v(C),$$ where summation is over all $n$-cells $C$ of the partition.
Definition. The average value of an $n$-form $f$ defined over a partition of an $n$-cell $B$ is defined to be: $$\text{average value of }f\ =\frac{1}{v(B)}\sum_{B}f\, \Delta V.$$
The limit of the Riemann sums, as the mesh of the partition is approaching $0$, is the Riemann integral. For all three dimensions, the integral of $f$ is the total weight: $$\begin{array}{llll} \text{weight }&=\int_{[a,b]}f(x)\, dx,\\ \text{weight }&=\iint_{[a,b]\times [c,d]}f(x,y)\, dxdy,\\ \text{weight }&=\iiint_{[a,b]\times [c,d]\times [p,q]}f(x,y,z)\, dxdydz.\\ \end{array}$$ Furthermore, the average density is the total amount (weight) divided by the measure of the “container”: $$\begin{array}{llll} \text{average density}&=\frac{1}{b-a}\int_{[a,b]}f(x)\, dx,\\ \text{average density}&=\frac{1}{(b-a)(d-c)}\iint_{[a,b]\times [c,d]}f(x,y)\, dxdy,\\ \text{average density}&=\frac{1}{(b-a)(d-c)(q-p)}\iiint_{[a,b]\times [c,d]\times [p,q]}f(x,y,z)\, dxdydz.\\ \end{array}$$ This is a launching pad into higher dimensions! We can now understand these three as one.
Definition. The average value of a function $z=f(X)$ of $n$ variables over an $n$-cell $B$ is defined to be: $$\text{average value of }f\ =\frac{1}{n\text{-volume of }B}\int_{B}f(X)\, dV.$$
Outside the sandbox
So far, the footprints of our solids are just rectangles. The example of the sphere in the beginning of the chapter shows that yet another generalization of the concept is needed: we need to be able to handle non-rectangular regions too.
The example also suggest the way to deal with this: we fill the missing values with $0$s.
Definition. Suppose a function $z=f(x,y)$ is defined over an arbitrary region $U$ in ${\bf R}^2$. Then the Riemann integral of $f$ over $U$ is defined to be the integral over any rectangle $R$ that contains $U$, $$\iint_Uf(x,y)\, dxdy=\iint_Rg(x,y)\, dxdy,$$ with the function $g$ defined by: $$g(x,y)=\begin{cases}f(x,y)&\text {inside }B,\\0&\text{outside }U;\end{cases}$$ when such integral exists, the function $f$ is called integrable over $U$.
Of course, this integral, and the area, might be infinite or not exist as all...
Furthermore, the ability to compute the volumes of complex solids presupposes the ability to compute the areas of complex plane regions!
But what is area anyway? The answer has been “the area under the graph of a function of one variable”. The answer leaves out a lot of regions such a disk. Fortunately, with the above definition we can have a double integral over any region $U$. In the simplest case we pick $f$ to be constant at $1$ over $U$. Then $$\text{the volume of }U\ =\ \text{ the area of }U\ \cdot \text{ the thickness}.$$
Definition. Suppose $U$ is a region in the plane. Then the area $A(U)$ of $U$ is defined to be the Riemann integral of the function equal to $1$ over $U$: $$A(U) =\iint_U 1\, dxdy.$$
Every integral is a limit and a limit might not exist; therefore, some regions have no areas!
Warning: it's not the same as to say that some regions have zero areas.
Note that the definition settles the debt from Chapter 13 about the meaning of the volume of a “shell”.
Thus we can finally put to rest the early idea we have relied on for so long that the area is a single integral; the area is a double integral! It's only when the region has a special shape, this double integral turns into a single one.
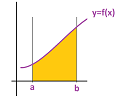
Indeed, let's match the new and the old definitions. Suppose $y=f(x)$ is a function. Then the area $U$ located under its graph between the lines $x=a$ and $x=b$ is: $$\int_a^b f\, dx\text{ but also } \iint_{U}1\, dxdy.$$
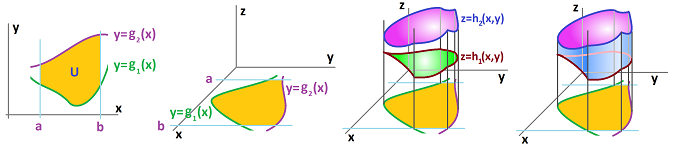
How do we represent this region $U$ algebraically? We know that $x$ runs between its bounds $a$ and $b$, what about $y$? Does it run between some $c$ and $d$? No, that would make $U$ a rectangle! The answer is: bounds on $y$, in the pair $(x,y)$, depends on $x$. In other words, we fix $x$ and look at all possible values of $y$: they lie between $0$ and $f(x)$. So, we have $$U=\{(x,y):a\le x\le b,\ 0\le y\le f(x)\}.$$ These four will serve as the bounds in our double integral in the new version of Fubini's Theorem. Let's carry out the computation to confirm the match: $$\begin{array}{lll} \iint_{U}1\, dxdy &= \int_{x=a}^{x=b}\left(\int_{y=0}^{y=f(x)}1\, dy\right)\, dx\\ &= \int_{x=a}^{x=b}\left( y \bigg|_{y=0}^{y=f(x)}\right)\, dx\\ &= \int_{x=a}^{x=b}\left( f(x)-0 \right)\, dx\\ &= \int_{a}^{b} f(x)\, dx,\ \text{ indeed!}\\ \end{array}$$
The case we will address is only slightly more complex.
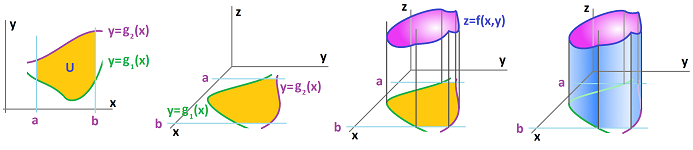
Theorem (Fubini's Theorem for two variables). Suppose $z=f(x,y)$ is a function integrable of the plane region given by $$\begin{array}{lll} U&=\{(x,y):&a\le x\le b,\\ &&g_1(x)\le y\le g_2(x)\}. \end{array}$$ Then $$\iint_{U}f\, dxdy = \int_{x=a}^{x=b}\left(\int_{y=g_1(x)}^{y=g_2(x)}f(x,y)\, dy\right)\, dx.$$
Proof.
$\blacksquare$
Just as before, the integral in the parentheses is the area $A(x)$ of the cross-section of the solid that lies above the region: $$\iint_{U}f\, dxdy = \int_{x=a}^{x=b}A(x)\, dx.$$ Therefore, the theorem is just a special case of the Cavalieri Principle.
So, to set up such an integral we should choose which of the two variables: $x$ is the independent variable and $y$ is the dependent. As an independent variable, $x$ can vary freely between two fixed numbers while the bounds for $y$ might depend on $x$.
Example. Let's go back to the beginning of the chapter and compute, exactly this time, the volume of the sphere of radius $R$. It is given by the implicit relation $x^2+y^2+z^2=R^2$. We represent the upper half of the sphere as the region bounded by the $xy$-plane from below and by the graph of the function from above: $$f(x,y)=\sqrt{R^2-x^2-y^2}.$$
Its domain is the “footprint”, or the shadow, of the surface: $$U=\{(x,y):x^2+y^2\le R^2\}.$$ It will also serve as the domain of integration!
But in order to apply Fubini's Theorem we need to represent it in the appropriate way, with explicit bounds for $x$ and $y$. First we include all possible values of $x$ and then, for a fixed $x$, we find the interval for $y$ (visible on the picture): $$\begin{array}{lll} U&=\{(x,y):&-R\le x \le R,\\ && -\sqrt{R^2-x^2}\le y \le \sqrt{R^2-x^2} \}. \end{array}$$ Now the volume is this integral: $$\begin{array}{lll} \text{volume }&=\iint_U\sqrt{R^2-x^2-y^2} dA&\text{ ... Fubini}\\ &= \int_{x=-R}^{x=R}\left(\int_{y=-\sqrt{R^2-x^2}}^{y=\sqrt{R^2-x^2}}\sqrt{R^2-x^2-y^2}\, dy\right)\, dx &\text{ ...a familiar integral}\\ &= \int_{x=-R}^{x=R}\left( \frac{y}{2}\sqrt{R^2-x^2-y^2} +\frac{R^2-x^2}{2}\sin^{-1}\frac{y}{R^2-x^2} \bigg|_{y=-\sqrt{R^2-x^2}}^{y=\sqrt{R^2-x^2}}\right)\, dx &\text{ }\\ &= \int_{x=-R}^{x=R}\frac{R^2-x^2}{2}(\pi/2-(-\pi/2))\, dx &\text{ }\\ &= \pi/2\int_{x=-R}^{x=R}(R^2-x^2)\, dx &\text{ }\\ &= \pi/2(R^2x-x^3/3)\bigg|_{x=-R}^{x=R} &\text{ }\\ &= \pi(R^2R-R^3/3) &\text{ }\\ &=\frac{2}{3}\pi R^3. \end{array}$$ The integral of $y$ in parentheses is for a fixed $x=c$ and represents the area of the corresponding cross-section of the half-sphere with this vertical plane. $\square$
Thus the complexity of solving such a problem lies more with finding the bounds of integration than the function to integrate. However, the task is familiar from Chapter 13.
Exercise. How much water is in a bucket that is tilted so the degree that makes the water to spill out? Solve (a) without integration, and (b) with integration.
Exercise. What geometric properties of the bucket allow one to solve the problem without integration?
Triple integrals
Definition. Suppose a function $z=f(X)$ is defined over an arbitrary region $U$ in ${\bf R}^n$. Then the Riemann integral of $f$ over $U$ is defined to be the integral over any box $B$ that contains $U$, $$\int_Uf(X)\, dV=\int_Bg(X)\, dV,$$ with the function $g$ defined by: $$g(X)=\begin{cases}f(X)&\text {inside }B,\\0&\text{outside }U;\end{cases}$$ when such integral exists, the function $f$ is called integrable over $U$.
Definition. Suppose $U$ is a region in ${\bf R}^n$. Then the $n$-volume $V(U)$ of $U$ is defined to be the Riemann integral of the function equal to $1$ over $U$: $$V(U) =\int_U 1\, dV.$$
Thus we can put to rest the recent idea that the volume is a double integral; the volume is a triple integral! It's only when the region has a special shape, this triple integral turns into a double one.
Indeed, let's match the new and the old definitions. Suppose $z=f(x,y)$ is a function. Then the 3d region $W$ located under its graph above a plane region $U$ is: $$\iint_U f\, dxdy\text{ but also } \iiint_{W}1\, dxdydz.$$
How do we represent this region $W$ algebraically? We know that $(x,y)$ runs within $W$, what about $z$? Does it run between some $p$ and $q$? No, that would make $W$ a cylinder! The answer is: the bound on $z$, in the triple $(x,y,z)$, depends on $(x,y)$. In other words, we fix $(x,y)$ in $U$ and look at all possible values of $z$: they lie between $0$ and $f(x,y)$. So, we have $$W=\{(x,y,z):(x,y)\text{ in }U,\ 0\le z\le f(x,y)\}.$$ Let's carry out the computation to confirm the match: $$\begin{array}{lll} \iiint_{W}1\, dxdydz &= \int_U\left(\int_{z=0}^{y=f(x,y)}1\, dz\right)\, dxdy\\ &= \int_U\left( z \bigg|_{z=0}^{z=f(x,y)}\right)\, dxdy\\ &= \int_U\left( f(x,y)-0 \right)\, dxdy\\ &= \int_U f(x,y)\, dxdy,\ \text{ indeed!}\\ \end{array}$$
The case we will address is only slightly more complex: instead of one surface bounding from above we have two bounding from above and below.
We accept the following without proof.
Theorem (Incremental Fubini's Theorem). Suppose $u=f(x,y,z)$ is a function integrable of the 3d region given by $$W=\{(x,y,z):(x,y) \text{ in } U,\ h_1(x,y)\le z\le h_2(x,y)\},$$ where $U$ is some plane region. Then $$\iiint_{W}f\, dxdydz = \int_U\left(\int_{z=h_1(x,y)}^{z=h_2(x,y)}f(x,y,z)\, dz\right)\, dxdy.$$
Let's make the region $U$ in the $xy$-plane specific. It is in fact identical to the one we considered above: bounded between two graphs: $$U=\{(x,y):a\le x\le b,\ g_1(x)\le y\le g_2(x)\}.$$ In other words, we take the $2$-dimensional Fubini's Theorem and add another integral in both left- and right-hand sides. The new integral -- with respect to $z$ -- will need its own bounds...
Theorem (Fubini's Theorem for three variables). Suppose $u=f(x,y,z)$ is a function integrable of the 3d region given by $$\begin{array}{lll} W&=\{(x,y,z):&a\le x\le b,\\ && g_1(x)\le y\le g_2(x),\\ && h_1(x,y)\le z\le h_2(x,y)\}. \end{array}$$ Then $$\iiint_{W}f\, dxdy = \int_{x=a}^{x=b}\left(\int_{y=g_1(x)}^{y=g_2(x)}\left(\int_{z=h_1(x,y)}^{z=h_2(x,y)}f(x,y)\, dz\right)\, dy\right)\, dx.$$
So, to set up such an integral we should choose the order of the three variables: $x$ is the independent variable, $y$ is dependent on $x$, and $z$ is dependent on $x$ and $y$. As an independent variable, $x$ can vary freely between two fixed numbers while the bounds for $y$ might depend on $x$ and the bounds for $z$ on both $x$ and $y$. The order of variables may change though...
Example. Let's take another look at the sphere. The computation of its volume in the last section -- as a double integral -- transforms into a new one -- as a triple integral. We consider the whole sphere this time (we don't have to rely on symmetry anymore!). We know that we represent the lower half and the upper half of the surface of the sphere as follows: $$h_1(x,y)=-\sqrt{R^2-x^2-y^2} \text{ and } h_2(x,y)=\sqrt{R^2-x^2-y^2}.$$
These will serve as the bounds for $z$! The other two come from the previous analysis of the circle:
Taken together they give us the region: $$\begin{array}{lll} U&=\{(x,y):&-R\le x \le R,\\ && -\sqrt{R^2-x^2}\le y \le \sqrt{R^2-x^2} ,\\ &&-\sqrt{R^2-x^2-y^2}\le z\le \sqrt{R^2-x^2-y^2}\}. \end{array}$$ Now the volume is this triple integral: $$\begin{array}{lll} \text{volume }&=\iiint_W 1\, dV\\ &= \int_{x=-R}^{x=R} \left( \int_{y=-\sqrt{R^2-x^2}}^{y=\sqrt{R^2-x^2}} \left( \int_{z=-\sqrt{R^2-x^2-y^2}}^{z=\sqrt{R^2-x^2-y^2}} 1\, dz \right) \, dy \right)\, dx \\ &= \int_{x=-R}^{x=R} \left( \int_{y=-\sqrt{R^2-x^2}}^{y=\sqrt{R^2-x^2}} \left( z\bigg|_{z=-\sqrt{R^2-x^2-y^2}}^{z=\sqrt{R^2-x^2-y^2}} \right) \, dy \right)\, dx \\ &= \int_{x=-R}^{x=R} \left( \int_{y=-\sqrt{R^2-x^2}}^{y=\sqrt{R^2-x^2}}2\sqrt{R^2-x^2-y^2}\, dy \right) \, dx . \end{array}$$ Except for $2$, this integral is identical to the integral in the last section. $\square$
The $n$-dimensional case
Theorem (Constant Integral Rule). Suppose $z=f(X)$ is constant on region $U$ in ${\bf R}^n$, i.e., $f(X) = m$ for all $X$ in $U$ and some real number $m$. Then $f$ is integrable over $U$ and $$\int_U f\, dV = m \cdot V(U).$$
The interpretation of additivity can be seen as the same as the one for numerical functions: the quantity in a region formed from two regions with a negligible overlap is equal to the sum of the quantities in the two.
- The two intervals overlap by a point, with zero length.
- The two rectangles overlap by an interval, with zero area.
- The two boxes overlap by a rectangle, with zero volume.
There is no double-counting in spite of overlapping!
Theorem (Additivity). Suppose $u=f(X)$ is integrable over regions $R$ and over $S$ in ${\bf R}^n$ and the two regions overlap only by their boundary points. Then $f$ is integrable $R\cup S$ and we have: $$\int_R f\, dV +\int_S f\, dV = \int_{R\cup S} f\, dV .$$
Theorem (Comparison Rule). If $$f(X)\geq g(X) \text{ on } U,$$ for some region $U$ in ${\bf R}^n$, then $$\int_U f\, dV \geq \int_U g\, dV ,$$ provided $u=f(X)$ and $u=g(X)$ are integrable functions over $U$. Otherwise we have: $$\begin{array}{lll} \int_U f\, dV =-\infty&\Longrightarrow& \int_U g\, dV =-\infty;\\ \int_U f\, dV =+\infty&\Longleftarrow& \int_U g\, dV =+\infty. \end{array}$$
Theorem (Estimate Rule) Suppose $u=f(X)$ is an integrable function over a region $U$ in ${\bf R}^n$. Then, if $$m \leq f(X)\leq M,$$ for all $X$ in $U$, we have $$m\cdot v(U)\leq \int_U f\, dV \leq M\cdot v(U).$$
Theorem (Constant Multiple Rule). Suppose $u=f(X)$ is an integrable function over a region $U$ in ${\bf R}^n$. Then so is $c\cdot f$ for any real $c$ and we have: $$ \int_U(c\cdot f)\, dV = c \cdot \int_U f\, dV.$$
Theorem (Sum Rule). Suppose $u=f(X)$ and $u=g(X)$ are integrable functions over region $U$ in ${\bf R}^n$. Then so is $f+g$ and we have: $$\int_U \left( f + g \right)\, dV = \int_U f\, dV + \int_U g\, dV . $$
The center of mass
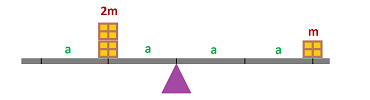
From Par II, we know how to balance this non-uniform rod on a single point of support:
The question is important because this point, called the center of mass, is the center of rotation of the object when subjected to a force.
The analysis follows one for the $1$-dimensional case; just all the numbers turn into vectors!
There are two (or more) axes this time.
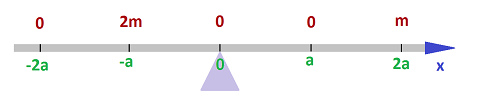
This is the $1$-dimensional balance equation: $$(a)(2m)=(2a)(m).$$
In other words, this expression: $$\text{ distance }\cdot \text{ weight },$$ called the moment, is the same to the left and to the right of the support. This distance, also called the lever, is now a vector! We simply re-write the balance equation: $$(-a)(2m)+(2a)(m)=0.$$
Then, $$\text{ moment }= \text{ vector of location }\cdot \text{ weight }.$$ Furthermore, we can assume there is an object at every location but the rest of them have $0$ mass. The balance equation becomes: $$...+(-2a)(0)+(-a)(2m)+(0)(0)+(a)(0)+(2a)(m)+...=0.$$
This analysis bring us to the idea of combining the weights and the distances in a proportional manner in order to evaluate the contribution of a particular weight to the overall balance. The balance equation simply says that the sum of all moments is $0$: $$\text{total moment } =\sum_i m_i A_i=0,$$ where $m_i$ is the weight of the object located at $A_i$.
We now go back to the original problem. Suppose different weights are located on a beam, where do we put the support in order to balance it?
It was entirely our decision to place the origin of our coordinate system at the center of mass. The result we have established should be independent from that choice and we can move the origin anywhere. We just need to execute a change of variables. Suppose the center of mass (and the origin of the old coordinate system) is located at the point with coordinate $Q$ of the new coordinate system. Then, the new coordinate of the object is $$C=A+Q.$$ Therefore, the balance equation has this form: $$\sum_C m_C (C-Q)=0.$$
Alternatively, we have: $$\sum_C m_C C=Q\sum_C m_C.$$ It's as if the whole weight is concentrated at $Q$. Hence the name.
Definition. We can call a system of weights a collection of non-negative numbers $m_C$ called weights assigned to each point $C$ in a collection of locations in ${\bf R}^n$. For a given point $Q$ and for each location $C$, the scalar product $$m_C(C-Q)$$ is called the corresponding object's moment with respect to $Q$. The sum of the moments $$\sum_C m_C (C-Q)$$ is called the total moment with respect to $Q$. The center of mass of this system of weights is such a location $Q$ that the total moment with respect to $Q$ is zero; i.e., $$c=\frac{\sum_C m_C C}{\sum_C m_C}.$$
Exercise. What if we allow the values of $m_C$ to be negative? What is the meaning of the system and of $Q$?
Suppose an augmented partition $P$ of a $n$-cell in ${\bf R}^n$ is given. Then the density $l$ is known and the terms $l(C)\Delta V_C$ are formed.
Each of these terms is a weight shown as a column. The lever of each is also shown as if the weight of the cell is concentrated at point $C$. Then the total moment of this system of weights with respect to some $Q$ is the Riemann sum, $$\sum_C m_C (C-Q)=\sum_C l(C)\Delta V (C-Q)=\sum_R G\, \Delta V,$$ of the vector-valued function of $n$ variables: $$G(X)=l(X)(X-Q).$$ Just as above, the system of weights that makes up the object is balanced when the total moment is zero. We arrive to a similar conclusion.
Theorem. Suppose $z=l(X)$ is a function of $n$ variables defined at points located at the $n$-cells of a partition of an $n$-cell $R$. Then the system of weights $l(X)\Delta X$ has its center of mass at the following point: $$Q=\frac{\sum_R l(X)X\, \Delta V }{\sum_R l(X) \, \Delta V }.$$
Example. Let's test this formula on some regions... $\square$
The next step is to think of the weights assigned to every location within $R$. It's a function!
What we have learned is that the total moment of the region with respect to some $Q$ is approximated by that of this system of weights, which is the Riemann sum, $$\sum_C m_C (C-Q)=\sum_C l(C_i)\Delta V (C-Q)=\sum_R G\, \Delta V,$$ of the vector valued function $$G(x)=l(X)(X-Q).$$ The system doesn't have to be balanced and the total moment doesn't have to be zero for each partition, but it does have to diminish to zero as we refine the partition. This means that the Riemann integral of this function is zero.
Definition. Suppose we have a non-negative function $z=l(X)$ integrable on region $R$ called the density function. For a given point $C$ and for each $X$, the vector-valued function $$Z=l(X)(X-Q)$$ is called the moment function with respect to $Q$. The integral of the moment function $$\int_R l(X)(X-Q)\, dV$$ is called the total moment of the segment with respect to $Q$. The center of mass of the segment is such a point $Q$ that the total moment with respect to $Q$ is zero.
Theorem. Suppose we have a non-negative function $z=l(X)$ integrable on region $R$. If the mass of $R$ is not zero, then the center of mass is located at: $$Q=\frac{\int_R l(X)X\, dV}{\int_R l(X)\, dV}.$$
Proof. First, we note that $Z=l(X)(X-C)$ is integrable by PR. Then we use SR and CMR to compute the following: $$0=\text{ total moment }=\int_R l(X)(X-C)\, dV=\int_R l(X)X\, dV+Q\int_R l(X)\, dV.$$ Now solve for $C$. $\blacksquare$
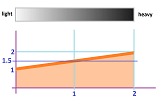
Example. Suppose the density of a $2\times 2$ plate $R$ is changing linearly: from $1$ to $2$, similar to this:
Then, $l(x)=x/2+y/2+1$ and the mass is: $$\begin{array}{ll} m=\int_R l(X)\, dV&=\int_{[0,1]\times[0,2]} (x/2+y/2+1)\, dV\\ &=\int_0^2 \int_0^2 (x/2+y/2+1)\, dxdy\\ &=\int_0^2 (x^2+xy/2+x)\big|_0^2\, dy\\ &= \end{array}$$ That's the denominator of the fraction. Now, we compute the numerator, the moment: $$\begin{array}{ll} M=\int_R l(X)X\, dV&=\int_R (x/2+y/2+1)<x,y>\, dV\\ &=\int_R <(x/2+y/2+1)x,(x/2+y/2+1)y>\, dV\\ &=<\int_R (x/2+y/2+1)x\, dV,\int_R (x/2+y/2+1)y\, dV>\\ &= \end{array}$$ Therefore, the center of mass is $$Q=\frac{M}{m}=.$$ $\square$
The expected value
Example. Let's recall the example of a baker the bread of whose is priced based on the prices of wheat and sugar that change every day. Every day for a month he recorded two numbers -- $x$ and $y$ -- that represent how much the two prices deviated from some minimum. And now he wants to understand what was the average combination of prices. For each combination of prices he records how many times is has occurred. He puts these numbers in a table, which makes a function of two variables. These may be its inputs and outputs: $$\begin{array}{l|cccc} y\backslash x&0&1&2&...&10\\ \hline 0&(0,0)&(0,1)&(0,2)&...&(0,10)\\ 1&(1,0)&(1,1)&(2,2)&...&(1,10)\\ 2&(2,0)&(1,1)&(2,2)&...&(2,10)\\ ...&...&...&...&...\\ 10&(10,0)&(10,1)&(10,2)&...&(10,10)\\ \end{array}\quad\leadsto\quad \begin{array}{l|cccc} y\backslash x&0&1&2&...&10\\ \hline 0&1&3&5&...&0\\ 1&2&4&6&...&0\\ 2&3&5&7&...&1\\ ...&...&...&...&...\\ 10&0&1&7&...&0\\ \end{array}$$ This may look like a generic function of two variables but let's take a closer look at how the data is collected. It's not the exact value of either price that matters but rather its range, say $2\le x<3$. This range is an interval of values and together the range of pairs of prices is a rectangle, say $[2,3]\times [1,2]$. The data then is represented by a table that looks a bit different: $$\begin{array}{l|cccc} y\backslash x&0&&1&&2&&3&...&9&&10\\ \hline 0&\bullet&--&\bullet&--&\bullet&--&\bullet&...&\bullet&--&\bullet\\ &|&1&|&3&|&5&|&...&|&0&|\\ 1&\bullet&--&\bullet&--&\bullet&--&\bullet&...&\bullet&--&\bullet\\ &|&2&|&4&|&6&|&...&|&0&|\\ 2&\bullet&--&\bullet&--&\bullet&--&\bullet&...&\bullet&--&\bullet\\ &|&3&|&5&|&7&|&...&|&1&|\\ 3&\bullet&--&\bullet&--&\bullet&--&\bullet&...&\bullet&--&\bullet\\ ...&&...&&...&&...&&...&&...\\ 9&\bullet&--&\bullet&--&\bullet&--&\bullet&...&\bullet&--&\bullet\\ &|&0&|&1&|&7&|&...&|&0&|\\ 10&\bullet&--&\bullet&--&\bullet&--&\bullet&...&\bullet&--&\bullet\\ \end{array}$$ We are justified to visualize this information as columns over these rectangles:
We realize that this isn't just a function of two variables; it's a discrete $2$-form! Furthermore, the average price combination is equivalent -- in the dimensions $1,2,3$ -- to finding the center of mass of this collection of bars.
$\square$
Gravity
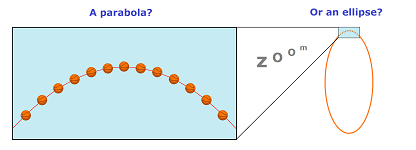
A familiar problem about a ball thrown in the air has a solution: its trajectory is a parabola. However, we also know that if we throw really-really hard (like a rocket) the ball will start to orbit the Earth following an ellipse.
The motion of two planets (or a star and a planet, or a planet and a satellite, etc.) is governed by a single force: the gravity. Recall how this force operates.
Newton's Law of Gravity: The force of gravity between two objects is given by the formula: $$F = G \frac{mM}{r^2},$$ where:
- $F$ is the force between the objects;
- $G$ is the gravitational constant;
- $m$ is the mass of the first object;
- $M$ is the mass of the second object;
- $r$ is the distance between the centers of the masses;
or, in the vector form (with the first object is located at the origin): $$F=-G mM\frac{X}{||X||^3}.$$
This is what we know.
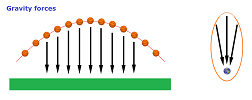
- When the Earth is seen as “large” in comparison to the size of the trajectory, the gravity forces are assumed to be parallel in all locations (the orbit is a parabola).
- When the Earth is seen as “small” in comparison to the size of the trajectory, the gravity forces are assumed to point radially toward that point (the orbit) may be an ellipse, or a hyperbola, or a parabola.
When the size and, therefore, the shape of the Earth matter, things get complicated...
Example.
This substitution for the simplest case of a perfectly spherical Earth is justified below.