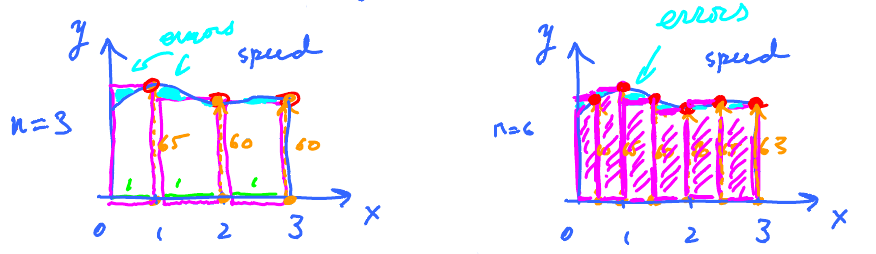Integral: introduction

This is what we have learned about the derivative:

• Geometrically, the derivative is about slopes.
• Algebraically, the derivative is about subtraction.

Indeed: $$\text{slope} = \frac{\text{rise}}{\text{run}} $$ and the numerator is the difference of the values of the function $f(b) - f(a)$.

Compare to differentiation and antidifferentiation: $$\left. \begin{aligned} \text{derivative: } \frac{df}{dx} \to \text{ difference } \to & \text{ subtraction } \\ & \downarrow \\ \text{anti-derivative: } \int f(x)dx \gets \text{ summation } \gets & \text{ addition } \end{aligned} \right. \text{opposite!}$$ The last one is called the integral.

Observations:

• It's the same "d" in "difference" and in $\frac{df}{dx}$.
• It's the same "s" in "summation" and in the integral sign $\int$.

Now where is the summation in antidifferentiation?

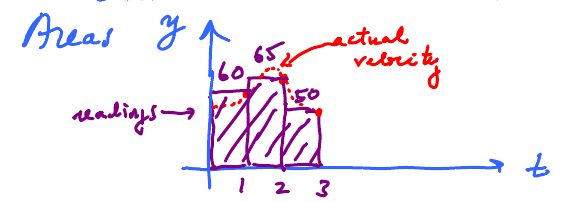
Consider again the example of the broken odometer. To know where you are, you have to use a watch and the speedometer. Suppose this is the record of your trip so far:

Speed	Time frame	Time length
60 m/h	1st hour	1
65 m/h	2nd hour	1
50 m/h	3rd hour	1

How far am I? $$\text{Distance covered } = 60 + 65 + 50 \qquad \text{(addition!)}. $$ But where's antidifferentiation?

We were given the velocity function, in the table, then we found the position function:

Velocity: $$ f(t) = \begin{cases} 60 & 0 \leq t < 1 \\ 65 & 1 \leq t < \\ 50 & 2 \leq t \leq 3 \end{cases} $$

Position: $$ F(t) = \begin{cases} 60t & 0 \leq t < 1 \\ 60 + 65(t-1) & 1 \leq t < 2 \\ & \text{etc}\ldots \end{cases} $$

Then $ F^{\prime} = f$ except for the special points. In other words, the position is an antiderivative of the velocity.

This is what we just learned about the antiderivative:

• Algebraically, the antiderivative is about addition.
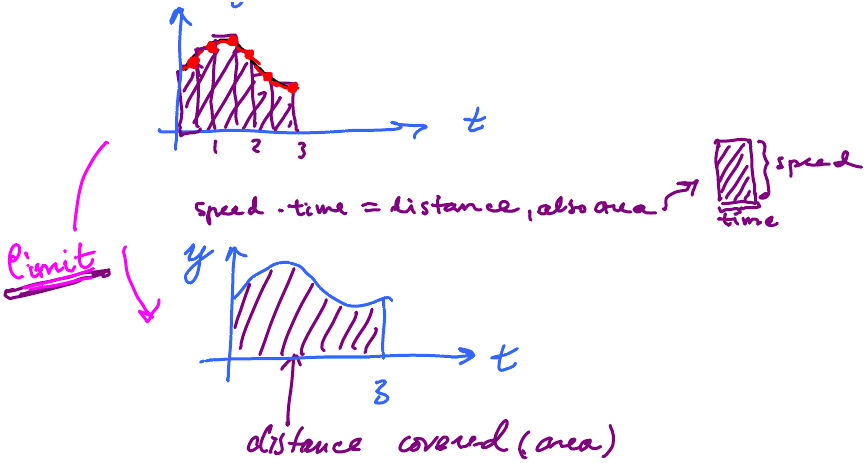
• Geometrically, the antiderivative is about areas.

Indeed:

Then, $$ \text{Distance } = 60 + 65 + 60 = \text{ Total of the three rectangles}. $$

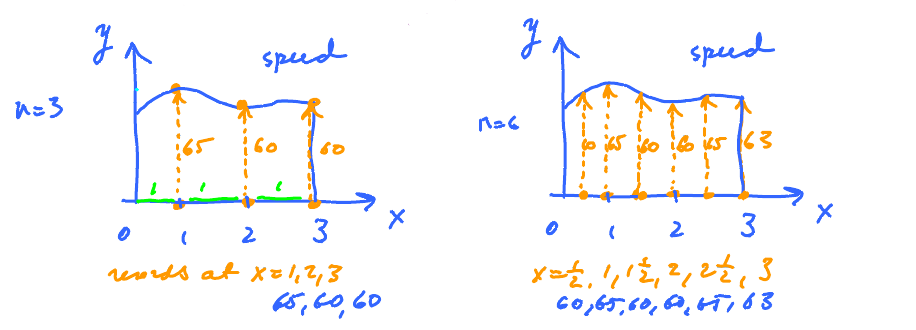
Let's take a reading of the speedometer every $\frac{1}{2}$ hour. Then estimate the distance. $$ D = 60\cdot \frac{1}{2} + 65\cdot \frac{1}{2} + 55\cdot \frac{1}{2} = \text{ Total area of these rectangles} $$

Let $n$ be the number of times we record speed.

The true, continuously changing velocity is found from this under the limit $\Delta x \to 0$ or $n \to \infty$.

As $n$ goes to $\infty$, the more rectangles we have and the thinner they are.

$$\begin{alignedat}{2} \text{distance } &\approx \underbrace{65 \cdot 1 + 60 \cdot 1 + 60 \cdot 1}_{\text{areas of rectangles}} & \qquad \text{distance } &\approx \underbrace{65 \cdot \frac{1}{2} + 65 \cdot \frac{1}{2} + 60 \cdot \frac{1}{2} + 65 \cdot \frac{1}{2} + 65 \cdot \frac{1}{2} }_{\text{areas of rectangles}} \end{alignedat} $$

How is the new data better?

The area under the graph is better approximated. In other words, the errors are smaller.

Idea: As $n \to \infty$, $\text{errors } \to 0$.

Now we realize:

 finding the position is equivalent to computing the area under the graph of the velocity.

See Integral: definition.