Integrability

Integrability*

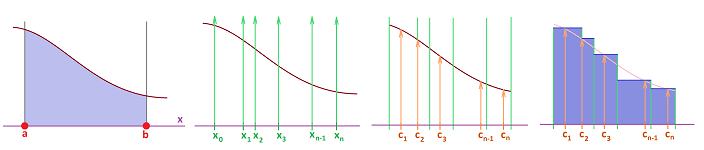
Recall that a augmented partition $P$ over interval $[a,b]$ consists of the nodes: $$a=x_0\le x_1\le x_2\le ...<x_{n-1}\le x_n=b,$$ and the secondary nodes: $$a=x_0\le c_1\le x_1\le c_2\le x_2\le ...<x_{n-1}\le c_1\le x_n=b.$$ Then the Riemann sum of a function $f$ over the augmented partition $P$ of an interval $[a,b]$ is defined to be $$\sum_a^b f_k \, \Delta x =\sum_{i=1}^{n} f(c_{i})\, \Delta x _i, $$ where $$\, \Delta x _i=x_i-x_{i-1}.$$

The mesh of a partition $P$ is: $$|P|=\max_i \, \, \Delta x _i.$$ It is a measure of “refinement” of $P$. We refine the partitions by requiring: $$|P| \to 0.$$

Then the Riemann integral of a function $f$ over interval $[a,b]$ is defined to be the number, denoted by $$ \int_{a}^{b} f\, dx =\lim_{k \to \infty} \sum_a^b f_k \, \Delta x ,$$ which is the limit of any sequence of its Riemann sums, whenever they all exist and are all equal to each other, with the mesh of their augmented partitions $P_k$ approaching $0$ as $k\to \infty$.

Theorem. A function $f$ is integrable on $[a,b]$ if and only if there is such a number $A$ that for any $\varepsilon >0$ there is a $\delta >0$ such that for any augmented partition $P$ with $|P|<\delta$ we have $$\left| \sum_a^b f\, \Delta x -A \right|<\varepsilon.$$ In that case, $$A=\int_{a}^{b} f\, dx.$$

Proof. $\blacksquare$

The left-end, right-end, and mid-point Riemann sums are simply the Riemann sums with secondary nodes specified ahead of time. Another way to do so is to choose these points to be maximum and minimum points of the function $$c_i=\arg\min_{[x_{i-1},x_i]} f \text{ and } C_i=\arg\max_{[x_{i-1},x_i]} f.$$ This is always possible whenever $f$ is continuous. Then we have two Riemann sums that satisfy: $$\sum_{i=1}^{n} f(c_{i})\, \Delta x _i \le \sum_a^b f\, \Delta x \le \sum_{i=1}^{n} f(c_{i})\, \Delta x _i, $$ for any other choice of secondary nodes for the same partition. If $f$ is bounded but not necessarily continuous, we still have: $$\sum_{i=1}^{n} m_{i}\, \Delta x _i \le \sum_a^b f\, \Delta x \le \sum_{i=1}^{n} M_{i}\, \Delta x _i, $$ where $$m_i=\inf_{[x_{i-1},x_i]} f \text{ and } M_i=\sup_{[x_{i-1},x_i]} f.$$

Definition. Given a bounded function $f$, the lower Darboux sum of $f$ over a partition $P$ of $[a,b]$ is defined to be $$\underline{S}_a^b(f,P) =\sum_{i=1}^{n} m_{i}\, \Delta x _i;$$ and the upper Darboux sum of $f$ is defined to be $$\bar{S}_a^b(f,P) =\sum_{i=1}^{n} M_{i}\, \Delta x _i.$$