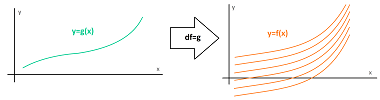Freshman's introduction to discrete calculus

Discrete functions

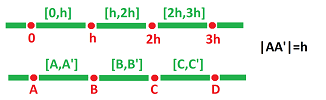
We divide the reals ${\bf R}$ into discrete pieces. To begin with, we divide it into intervals of equal length $h>0$:

The result is two types of pieces:

• nodes $A=...-2h,-h,0,h,2h,3h, ...$; and
• edges $[A,B]=...[-2h,-h],[-h,0],[0,h],[h,2h],...$.

They will not be intermixed in computations.

For the sake of simplicity, below we illustrate mostly the case of $$h=1.$$ In that case, we have

• nodes $A=...,-2,-1,0,1,2,3, ...$; and
• edges $[A,B]=...,[-2,-1],[-1,0],[0,1],[1,2],...$.

Furthermore, there are two types of discrete functions:

• node functions with nodes as inputs; and
• edge functions with edges as inputs.

The outputs are real numbers.

We use arrows to picture these functions as correspondences:

Here we have two:

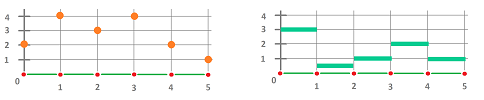
• a node function $f: 0\mapsto 2,\ 1\mapsto 4,\ 2\mapsto 3, ...$; and
• an edge function $s: [0,1]\mapsto 3,\ [1,2]\mapsto .5,\ [2,3]\mapsto 1, ...$.

A more compact way to visualize is this:

We can also list the values of the two discrete functions:

• a node function $f$ with $f(0)=2,\ f(1)=4,\ f(2)=3,\ ...$; and
• a edge function $s$ with $s\Big([0,1] \Big)=3,\ s\Big([1,2] \Big)=.5,\ s\Big([2,3] \Big)=1,\ ...$.

We also use letters to label the pieces. Each is then assigned two symbols: one is its name (a latter) and the other is the value of the discrete function at that location (a number):

Here we list the values again:

• $f(A)=2,\ f(B)=4,\ f(C)=3,\ ...$;
• $s([A,B])=3,\ s([B,C])=.5,\ s([C,D])=1,\ ...$.

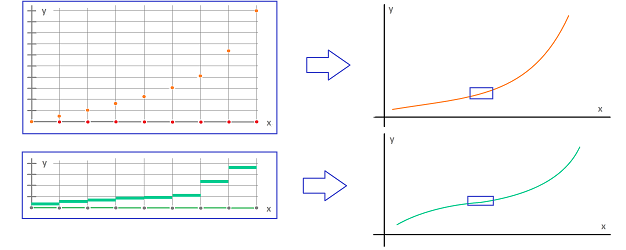
Even though these functions are made of unrelated pieces, it is possible that we can see continuous curves if we zoom out:

If we zoom in, we can fill in the gaps...

Theorem (Intermediate Value Theorem). Given a node function $f$, if a real number $c$ satisfies $$f(a)<c<f(b)$$ for some nodes $a,b$, then there is a edge $[A,A']$ located between the nodes $a,b$ and there is a real number $t$ with $0\le t\le 1$ such that $$c=(1-t)f(A)+tf(A').$$

Discrete functions can be represented by tables, see Spreadsheets.

The integral

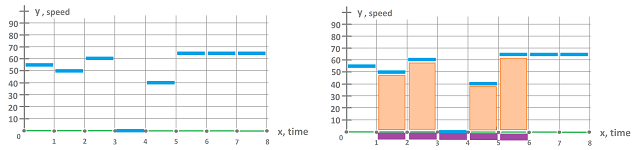
Let's consider a simple situation. A person drove for $8$ hours. What happened during each hour is known; he covered the following distance: $$\begin{array}{l|c|c|c|c|c|c|c|c} \text{hour} &1 &2 &3 &4 &5 &6 &7 &8\\ \hline \text{distance} &55&50&60&0 &40&65&65&65 \end{array}$$

We represent the distances as an edge function $s$:

The values of this function $s$ is known for the single edges: $$s\Big( [0,1]\Big)=55,\ s\Big([1,2]\Big)=50,\ s\Big([2,3]\Big)=60,\ ...$$

Now, what is the distance covered by the driver during $2-6$ hours?

We represent this time interval as a “chain” of edges, $$a=[1,5]=[1,2]\cup [2,3]\cup [3,4]\cup [4,5].$$ Then the distance is simply the sum: $$\begin{array}{lllll} s(a)&=s\Big( [1,2] \cup [2,3] \cup [3,4] \cup [4,5] \Big)\\ &=s\Big( [1,2] \Big)+s\Big( [2,3] \Big)+s\Big( [3,4] \Big)+s\Big( [4,5] \Big)\\ &=50+60+0+40\\ &=150. \end{array}$$ We think of the answer as the displacement of an object that moves with speed given by $s$ over a period of time represented by $a$.

Definition. Given two nodes $A,B$ with $A<B$, the integral of an edge function $s$ over the interval $[A,B]$ is defined to be the sum of its values over the interval: $$\displaystyle\int_{[A,B]} s:= s\Big( [A,A_1] \Big)+...+s\Big( [A_n,B] \Big),$$ where $A_1,...,A_n$ are the consecutive nodes between $A$ and $B$.

Alternative notation is: $$\displaystyle\int_A^B s.$$

As we can see, the integral of $s$ is the area of the graph of $s$ that lies over $a$.

If we zoom put, it might appear that we can compute the areas of more complex, curved regions, even if they are still made of nothing but rectangles:

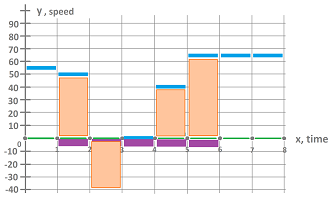
Furthermore, if the person drove for an hour in the opposite direction and covered $40$ miles, the data becomes: $$\begin{array}{l|c|c|c|c|c|c|c|c} \text{hour} &1 &2 &3 &4 &5 &6 &7 &8\\ \hline \text{distance} &55&-40&60&0 &40&65&65&65 \end{array}$$

Then, we still find the displacement by adding these values: $$\begin{array}{lllll} s(a)&=s\Big( [1,2] \cup [2,3] \cup [3,4] \cup [4,5] \Big)\\ &=s\Big( [1,2] \Big)+s\Big( [2,3] \Big)+s\Big( [3,4] \Big)+s\Big( [4,5] \Big)\\ &=50+(-40)+0+40\\ &=50. \end{array}$$

To capitalize on this idea even further, we extend the meaning of the integral to include “reversed” intervals.

Definition. Given two nodes $A,B$ with $A<B$, the integral of an edge function $s$ over the interval $[B,A]$ is defined to be the negative sum of its values over the interval: $$\displaystyle\int_{[B,A]} s:= -\Big( s\big( [A,A_1] \big)+...+s\big( [A_n,B] \big) \Big),$$ where $A_1,...,A_n$ are the consecutive nodes between $A$ and $B$.

File:Integral on reversed interval.png

In other words, we have: $$\int\limits_{[B,A]} s := -\int\limits_{[A,B]} s.$$ It is as if time goes backward and all gains are reversed...

The integrals are evaluated with Spreadsheets.

There are no integrals of node functions.

Properties of the integral

The main property of the integral follows from the definition.

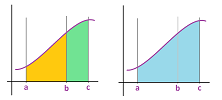
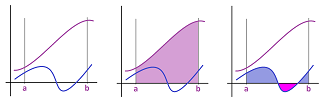
Theorem (Additivity). Suppose $s$ is an edge function. For any nodes $a,b,c$ with $a<c$, we have: $$\int\limits_{[a,b]} s +\int\limits_{[b,c]} s = \int\limits_{[a,c]} s.$$

The area interpretation of additivity is illustrated below:

Here we have simply, $$\begin{array}{lll} \int_{a}^{b} s &+& \int_{b}^{c} s &=& \int_{a}^{c} s,\\ orange&+&green&=&blue. \end{array}$$

With the motion interpretation of integral, we have: $$\begin{array}{lll} &\text{distance covered during the 1st hour }\\ +&\text{distance covered during the 2nd hour }\\ =&\text{distance during the two hours}. \end{array}$$

Theorem (Comparison). (1) Suppose $s$ is an edge function. For any nodes $a,b$ with $a<b$, if $s(x) \geq 0$ on $[a,b]$ then $$ \int_{a}^{b} s \geq 0. $$ (2) Suppose $s$ and $t$ are edges functions. For any nodes $a,b$ with $a<b$, if $s(x) \geq t(x)$ on $[a,b]$ then $$\int_{a}^{b} s \geq \int_{a}^{b} t.$$

Motion interpretation: faster covers longer distance.

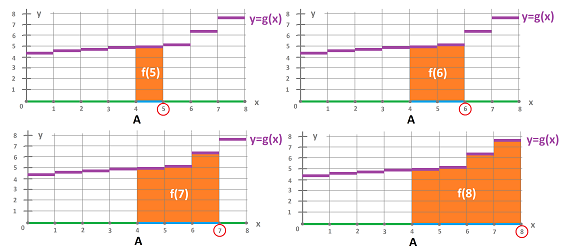
What if we know only estimates of $f$? Like this: $$m \leq s(x) \leq M,$$ for all $x$ in $[a,b]$. Then what? We want to find an estimate for the area of the orange region in terms of $a$, $b$, $m$, $M$. Below, the yellow region on the left is less then the orange area. On the right, the green area is larger. But these regions are rectangles and their areas are easy to compute.

$$\text{the area of the smaller rectangle}\leq \text{the area under the graph} \leq \text{the area of the larger rectangle}.$$ Hence, we have the following.

Theorem (Estimate). Suppose $s$ is an edge function. For any nodes $a,b$ with $a<b$, if $$m \leq s(x) \leq M,$$ for all $x$ in $[a,b]$, then $$m(b-a)\leq \int_{a}^{b} s \leq M(b-a).$$

Finally, these are the algebraic properties.

Theorem (Constant function rule). For any nodes $a,b$ and any real $c$, we have: $$\int\limits_{a}^{b} c = c \left( b-a \right). $$

Theorem (Constant multiple rule). Suppose $s$ is an edge function. For any nodes $a,b$ and any real $c$, we have: $$ \int_{a}^{b} c\, s = c \, \int_{a}^{b} s.$$

Theorem (Sum Rule). Suppose $s$ and $t$ are edge functions. For any nodes $a,b$, we have: $$\int_{a}^{b} \left( s + t \right) = \int_{a}^{b} s + \int_{a}^{b} t. $$

The differential

We next study the change of node functions.

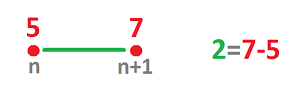
Let's consider an example of motion. Suppose a node function $p$ gives the position of a person and suppose

• at time $n$ hours we are at the $5$ mile mark: $p(n)=5$, and then
• at time $n+1$ hours we are at the $7$ mile mark: $p(n+1)=7$. $\\$

We don't know what exactly has happened during this hour but the simplest assumption would be that we have been walking at a constant speed of $2$ miles per hour. Now, instead of our velocity function $v$ assigning this value to each instant of time during this period, it is assigned to the whole interval: $$v\Big( [n,n+1] \Big)=2.$$ This way, the elements of the domain of the velocity function are the edges and the resulting function is an edge function.

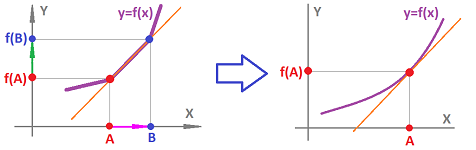
Node functions are defined on the nodes, such as: $$A=...-1,0,2,3,4, ....$$ They change abruptly and, consequently, the change over every edge $[A,B]$ is simply the difference of values: $$f(B)-f(A).$$

The output of this simple computation is assigned to the edge $[A,B]$: $$[A,B] \mapsto f(B)-f(A).$$

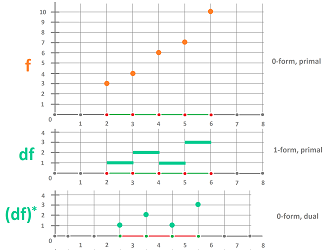
The relation between a node function and its change is illustrated below:

Definition. The differential of a node function $f$ at edge $[A,B]$ is defined to be the number $$(df) \big([A,B] \big):=f(B)-f(A).$$

Thus, we have:

• $f$ is defined on the nodes, and
• $df$ is defined on the edges.

The latter is a new edge function!

Definition. The differential of a node function $f$ is an edge function denoted by $df$ given by its values on each edge: $$(df) \big([x,x+h] \big):=f(x+h)-f(x).$$

The differentials can be computed for node functions given by tables, see Spreadsheets.

Example. When the node functions are represented by formulas, the computations are straightforward ($h=1$): $$\begin{array}{lll} f(n)=3n^2+1\ \Longrightarrow\ &(df)\big( [n,n+1] \big)=(3(n+1)^2+1)-(3n^2+1)=6n+3;\\ g(n)=\frac{1}{n}\ \Longrightarrow\ &(dg)\big( [n,n+1] \big)= \frac{1}{n+1}-\frac{1}{n}=-\frac{1}{n(n+1)};\\ p(n)=2^n\ \Longrightarrow\ &(dp)\big( [n,n+1] \big)= 2^{n+1}-2^{n}=2^n. \end{array}$$ $\square$

There are a few simple facts about the differential.

Theorem (Monotonicity). A node function is increasing (decreasing) on an interval if and only if its differential is positive (negative) on each edge in this interval; i.e., $$f\nearrow \text{ on } [a,b]\ \Longleftrightarrow\ (df) \big([x,x+h]\big) >0\text{ whenever } a \le x < x+h \le b;$$ and $$f\searrow \text{ on } [a,b]\ \Longleftrightarrow\ (df) \big([x,x+h]\big) <0\text{ whenever } a \le x < x+h \le b.$$

The proof is elementary: $$f(x+h)>f(x)\ \Longleftrightarrow\ f(x-h)-f(x)>0.$$ However, zooming out shows the meaningfulness of the theorem:

Example. We can also use algebra to find out how the function behaves: $$\begin{array}{lll} f(n)=3n^2+1\ \Longrightarrow\ &(df)\big( [n,n+1] \big)=6n+3\ \Longrightarrow\ &f\searrow \text{ on } (-\infty,2],\ f\nearrow \text{ on } [2,\infty);\\ g(n)=\frac{1}{n}\ \Longrightarrow\ &(dg)\big( [n,n+1] \big)=-\frac{1}{n(n+1)}\ \Longrightarrow\ &g\searrow \text{ on } (-\infty,-1],\ g\searrow \text{ on } [1,\infty);\\ p(n)=2^n\ \Longrightarrow\ &(dp)\big( [n,n+1] \big)=2^n\ \Longrightarrow &p\nearrow \text{ on } (-\infty,\infty). \end{array}$$ With just this data we can sketch very rough graphs of these three functions:

$\square$

Corollary (Extreme Values). A node function has a local maximum (minimum) at a point if and only if its differential is positive (negative) to the point's left and negative (positive) to its right; i.e., $$c \text{ is a local maximum of }f\ \Longleftrightarrow (df) \big([c-h,c]\big) >0 \text{ and } (df) \big([c,c+h]\big) <0;$$ and $$c \text{ is a local minimum of }f\ \Longleftrightarrow (df) \big([c-h,c]\big) <0 \text{ and } (df) \big([c,c+h]\big) >0.$$

Theorem (Constant Function). A node function is constant on an interval if and only if its differential on each edge in this interval is zero; i.e., $$f=const \text{ on } [a,b]\ \Longleftrightarrow (df) \big([x,x+h]\big) =0 \text{ whenever } a\le x < x+h\le b.$$

Corollary. Two node functions have the same differential on an interval if and only if their differ by a constant on that interval; i.e., $$df =dg \text{ on } [a,b]\ \Longleftrightarrow f=g+c \text{ for some real } c \text{ on } [a,b].$$

There are no differentials of edge functions.

Algebraic properties of the differential

Theorem (Sum Rule). For any two node functions $f,g$, we have: $$d(f + g)= df + dg.$$

Theorem (Constant Multiple Rule). For any node function $f$ and any real $c$, we have: $$d(cf) = c\, df.$$

Theorem (Power Formula). For any positive integer $k$ and any edge $[n,n+1]$, we have: $$d (n^{\underline {k}})\big([n,n+1]\big)=kn^{\underline {k-1}},$$ where $$p^{\underline {q}} := p(p-1)(p-2)(p-3)...(p-q+1). $$

Proof. From the definition, we have: $$\begin{array}{lll} d (x^{\underline {k}})\big([n,n+1]\big)&=d\big( n(n-1)(n-2)...(n-k+1) \big)\\ &=(n+1)n(n−1)...(n−k+2)−n(n−1)(n−2)...(n−k+2)(n−k+1) \\ &= n(n−1)...(n−k + 2)(n + 1 − (n − k + 1)) \\ &= kn^{\underline {k-1}} . \end{array}$$ $\square$

Theorem (Exponent Formula). For any positive real $b$ and any edge $[n,n+1]$, we have: $$d(b^n)\big([n,n+1]\big)=(b-1)b^n.$$

Exercise. Prove these theorems.

Theorem (Trig Formulas). For any real $t$ and any edge $[n,n+1]$, we have: $$\begin{array}{lllll} d(\sin (tA))\big([n,n+1]\big)=2\sin \big(\tfrac{t}{2}\big) \cos \big(t(n+\tfrac{1}{2})\big),\\ d(\cos (tA))\big([n,n+1]\big)=-2\sin \big(\tfrac{t}{2}\big) \sin \big(t(n+\tfrac{1}{2}\big)). \end{array}$$

Proof. We use the formulas: $$\begin{array}{lllll} \sin u - \sin v = 2 \sin\big(\tfrac{1}{2}(u-v)\big) \cos\big(\tfrac{1}{2}(u+v)\big);\\ \cos u + \cos v = -2 \sin\big(\tfrac{1}{2}(u-v)\big) \sin\big(\tfrac{1}{2}(u+v)\big). \end{array}$$ Then $$d(\sin tn)\big([n,n+1]\big)=\sin \big(t(n+1)\big) - \sin (tn) = 2 \sin\big(\tfrac{1}{2}t\big) \cos\big(\tfrac{1}{2}t(2n+1)\big).$$ $\square$

Exercise. Finish the proof.

Theorem (Product Rule). Given two node functions $f,g$, for any edge $[n,n+1]$, we have: $$d(f \cdot g)\big([n,n+1]\big) = f(n+1)dg\big([n,n+1]\big) + df\big([n,n+1] \big)g(n).$$

Proof. $$\begin{array}{lll} d(f \cdot g)\big([n,n+1]\big)&=(f \cdot g)(n+1)- (f \cdot g)(n)\\ &=f(n+1) \cdot g(n+1)- f(n) \cdot g(n)\\ &=f(n+1) \cdot g(n+1)- f(n+1) \cdot g(n) +f(n+1) \cdot g(n)- f(n) \cdot g(n)\\ &=f(n+1) \cdot (g(n+1)- g(n)) +(f(n+1) - f(n)) \cdot g(n)\\ &=f(n+1)dg\big([n,n+1]\big) + df\big([n,n+1] \big)g(n). \end{array}$$ $\square$

Theorem (Quotient Rule). Given two node functions $f,g$ and any edge $[n,n+1]$, we have: $$d(f/g)([n,n+1]) = \frac{df\big([n,n+1] \big)g(n) - f(n+1)dg\big([n,n+1] \big)}{g(n)g(n+1)},$$ provided $g(n),g(n+1) \ne 0$.

There are no, in general, compositions of node functions and, therefore, no chain rule.

Exercise. Prove this theorem by following the proof for the Product Rule.

Exercise. Derive the “Power Formula” for $k<0$.

Exercise. Derive the “Log Formula”: $d(\log_b (tn)) \big([n,n+1] \big)=$?

The Fundamental Theorem of Calculus

We now consider the relation between the integral and the differential.

Given a node function $f$, let's take our definition of the differential $df$, $$df\big([A,B] \big) :=f(B) - f(A),$$ and integrate this edge function over the same edge. Since there is only one interval here, the result is trivial: $$\displaystyle\int_{[A,B]} df = f(B) - f(A).$$

Now, what about integration over “longer” intervals? Let $A_0,A_1,...,A_k$ is a sequence of consecutive nodes. Let's consider the interval as a “chain” of edges: $$[A_0,A_k] := [A_0,A_1] \cup [A_1,A_2] \cup ... \cup [A_{k-1},A_k].$$ Then we have: $$\begin{array}{llll} \int_{[A_0,A_k]} df &= df\big([A_0,A_1]& \cup [A_1,A_2]& \cup ...& \cup [A_{k-1},A_k] \big) \\ &= df\big([A_0,A_1] \big)&+df\big([A_1,A_2] \big)&+...&+df\big([A_{k-1},A_k] \big) \\ &= f(A_1)-f(A_0) &+ f(A_2) - f(A_1) &+ ... &+ f(A_k) - f(A_{k-1}) \\ &= f(A_k) -f(A_0) . \end{array}$$ We simply applied the definition repeatedly.

Theorem (Fundamental Theorem of Calculus). Given a node function $f$, we have for every pair of nodes $A,]$, $$\begin{array}{|c|} \hline \\ \quad \displaystyle\int_{[A,B]} df =f(B) -f(A). \quad \\ \\ \hline \end{array}$$

This is the theorem's “net change” form.

Here is another form of the Fundamental Theorem.

Theorem. Let $g$ be an edge function. Suppose a node $A$ is fixed. Define a node function $f$ by giving it a value for every node $B$, $$f(B):=\int_{[A,B]} g.$$ Then $$df=g.$$

Theorem. Given an edge function $g$, any node function with $df=g$ is found by the formula given in the theorem, for some node $A$.

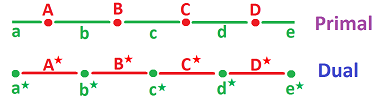
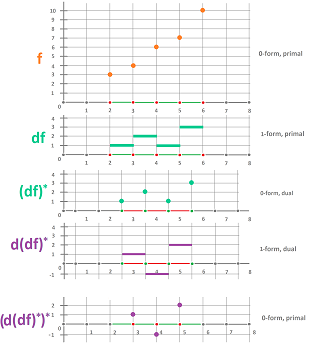
Primal and dual domains

Further, we are to study the change of functions in a more quantitative way.

We notice that our discrete version of the reals doesn't faithfully represent ${\bf R}$. The good news is, the edges are attached to each other at the nodes to form a continuous curve. However, it is a straight line?

Let's look at the domain as a combination of hinges and rods. Together they constitute one object but it is not rigid!

To make the contraption rigid -- and straight -- we add an identical copy and attach each new hinge in the middle of an old rod:

Thus there are a new node for each edge in the domain and a new edge for each node. Together, these new nodes and edges form a new copy of the domain.

This is how the cells of the two are matched:

• an edge $a$ in the domain corresponds to a new node $a^\star$; and
• a node $A$ in the domain corresponds to a new edge $A^\star$. $\\$

We have a correspondence between the pieces of the original, called primal, domain and those of the new, called dual, domain:

• each primal node corresponds to a dual edge, and
• each primal edge corresponds to a dual node.

Furthermore, the correspondence (primal to dual):

• the dual of a primal node is a dual edge, and
• the dual of a primal edge is a dual node;

can be reversed (dual to primal):

• the dual of a dual node is a primal edge, and
• the dual of a dual edge is a primal node.

This two-directional correspondence, $a\mapsto a^\star$, is called duality. An important fact to remember is the following.

Proposition. For a primal (or dual) node (or edge) $a$, we have $$a^{\star\star}=a.$$

Next, just as we specified the locations of the primal nodes: $$...,x-2h,x-h,x,x+h,x+2h,...;$$ we can also specify the dual nodes: $$...,x-3h/2,x-h/2,x+h/2,x+3h/2,x+5h/2,....$$

Proposition. (1) For every primal node $x$, its dual is the dual edge centered at $x$, i.e., $$x^\star = [x-h/2,x+h/2].$$ (2) For every primal edge $[x,x+h]$, its dual is the dual node at its center, i.e., $$[x,x+h]^\star = x+h/2.$$

Let's reverse the correspondence in the proposition. Then, for every dual node $z$, we have $$z^\star = [z-h/2,z+h/2];$$ and for every dual edge $[z,z+h]$, we have $$[z,z+h]^\star = z+h/2.$$ This fact is restated as follows.

Proposition. (1) For every dual node $x+h/2$, its dual is the primal edge centered at $x$, i.e., $$(x+h/2)^\star = [x,x+h].$$ (2) For every dual edge $[x-h/2,x+h/2]$, its dual is the primal node at its center, i.e., $$[x-h/2,x+h/2]^\star = x.$$

The new domain is a full copy of the old domain. The new domain has the full set of node and edge functions. They are called dual while the original ones are called primal functions. The differential is also known, $d$.

There is a direct relation between these functions. The new function is given by the same formula and only the input variable is replaced, e.g., a primal node function $y=f(x)=x^2$ is replaced with a dual edge function $g\big( [x-h/2,x+h/2] \big)=f(x)=x^2$.

Proposition. Given a primal node/edge function $s$, the following is a dual edge/node function: $$s^\star (a):=s(a^\star).$$

Then, $s^\star$ is called the dual function of $s$.

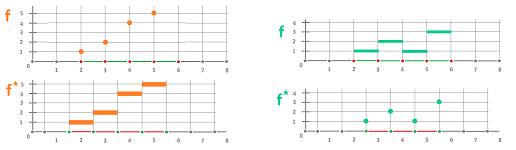
Two dual pairs are illustrated below:

If we zoom out, the dual functions will look identical!

The relation between these two calculi is seen in the following duality diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{rccc} \text{Primal domain: }& \text{ node function }& \ra{\quad d\quad }& \text{ edge function } &\\ &\ua{\star} & \ne & \da{\star} & \\ \text{Dual domain: } & \text{ edge function }& \la{\quad d\quad } & \text{ node function }& \\ \end{array} $$ Note that we do not claim that making the full circle will give us the function we started with.

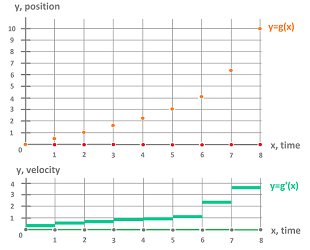
The derivative

The ability to measure distances in the domain allows us to study “the rate of change” of a node function instead of just “change”, which is the differential.

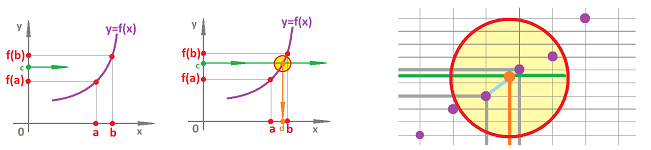
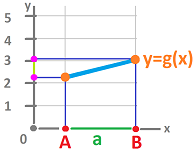
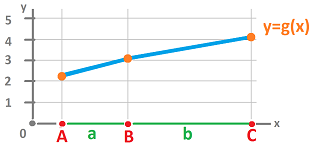
For a node function $y=g(x)$, as if it is linear on interval $[A,B]$, its rate of change is defined to be $$\frac{\text{change of } y}{ \text{change of } x}=\frac{g(B)-g(A)}{B-A}.$$ The ration is also known as the slope of the line.

We can re-write the fraction as $$\frac{g(B)-g(A)}{B-A} = \frac{g(B)-g(A)}{|[A,B]|}= \frac{g(B)-g(A)}{h}.$$ The numerator is easily recognized as $dg(a)$, the differential $dg$ of the node function $g$ evaluated at the edge $a=[A,B]$.

Now, to create a new function, we need assign this new number, the output, to an input? Is it an edge or a node, primal or dual? We assign the value of the above ratio to the node dual to $a$, as follows.

Definition. The derivative of a primal node function $g$ is the dual node function given by its values at each dual node, $P$: $$g'(P):=\frac{1}{h}dg(P^\star).$$

Alternatively, we have $$g'( x+h/2 ):=\frac{1}{h}dg\big([x,x+h]\big).$$ Also useful is the explicit form: $$g'( x+h/2 ):=\frac{g(x+h)-g(x)}{h}.$$ We can also switch from the primal to the dual domain as a reference, with the substitution: $$z=x+h/2,\quad x=z-h/2.$$ Then we have: $$g'( z ):=\frac{g(z+h/2)-g(z-h/2)}{h}.$$

As a node function, the derivative can be further differentiated, as discussed in the next subsection.

This is how the definition works:

When the node function is represented by a formula, the computation is often straightforward.

Example. (1) $$\begin{array}{lll} f(x)=3x^2+1\ &\Longrightarrow\ \\ f'(x+h/2)&=\frac{1}{h}\big(3(x+h)^2+1)-(3x^2+1)\big)\\ &=\frac{1}{h}\big((3x^2+6xh+3h^2+1)-(3x^2+1) \big)\\ &=\frac{1}{h}(6xh+3h^2)\\ &=6x+3h \ \Longrightarrow \\ f'( z )&=6(z-h/2)+3h\\ &=6z. \end{array}$$ (2) $$\begin{array}{lll}g(x)=\frac{1}{x}\ &\Longrightarrow\ \\ g'(x+h/2)&= \frac{1}{h}\left( \frac{1}{x+h}-\frac{1}{x} \right)\\ &= \frac{1}{h}\left( \frac{x}{x(x+h)}-\frac{x+h}{x(x+h)} \right)\\ &=\frac{1}{h}\frac{-h}{x(x+h)}\\ &=-\frac{1}{x(x+h)}\ \Longrightarrow\\ g'( z )&=-\frac{1}{(z-h/2)(z-h/2+h)}\\ &=-\frac{1}{(z-h/2)(z+h/2)}. \end{array}$$ (3) $$\begin{array}{lll} p(x)=2^x\ &\Longrightarrow\ \\ p'(x+h/2)&= \frac{1}{h}(2^{x+h}-2^{x})\\ &=\frac{1}{h}2^{x}(2^h-1)\\ &=\frac{2^h-1}{h}2^x \ \Longrightarrow\\ p'( z )&=\frac{2^h-1}{h}2^{z-h/2}. \end{array}$$ $\square$

Further, for node functions $f$ and $g$, we have $$f'=g' \Longleftrightarrow df=dg.$$ Secondly, the sign of the differential and that of the derivative coincide. These two facts allow us to restate the simple calculus theorems about the differential.

Theorem (Monotonicity). A node function is increasing (decreasing) on an interval if and only if its derivative is positive (negative) on each edge in this interval; i.e., $$f\nearrow \text{ on } [a,b]\ \Longleftrightarrow\ f' ( x+h/2 ) >0\text{ whenever } a \le x < x+h \le b;$$ and $$f\searrow \text{ on } [a,b]\ \Longleftrightarrow\ f' ( x+h/2 ) <0\text{ whenever } a \le x < x+h \le b.$$

Zooming out shows the meaning of the theorem:

Corollary (Extreme Values). A node function has a local maximum (minimum) at a point if and only if its derivative is positive (negative) to the point's left and negative (positive) to its right; i.e., $$c \text{ is a local maximum of }f\ \Longleftrightarrow f' ( c-h/2 ) >0 \text{ and } f' ( c+h/2 ) <0;$$ and $$c \text{ is a local minimum of }f\ \Longleftrightarrow f' ( c-h/2 ) <0 \text{ and } f' ( c+h/2 ) >0.$$

Theorem (Constant Function). A node function is constant on an interval if and only if its derivative on the dual of each edge in this interval is zero; i.e., $$f=const \text{ on } [a,b]\ \Longleftrightarrow f'( x+h/2 ) =0 \text{ whenever } a\le x < x+h\le b.$$

Corollary. Two node functions have the same derivative on an interval if and only if their differ by a constant on that interval; i.e., $$f' =g' \text{ on } [a,b]\ \Longleftrightarrow f=g+c \text{ for some real } c \text{ on } [a,b].$$

The derivative is computed with a spreadsheet:

Link to file: Spreadsheets.

The derivative also gives us the slope of the line that -- when zoomed out -- appear to touch the graph at the point. That is why the line is called a tangent line.

There are no derivatives of edge functions.

Algebraic properties of the derivative

The formula is simple. Then, the Sum Rule, the Constant Multiple Rule, the Product Rule, and the Quotient Rule all hold without change. Furthermore, the denominator is the only thing we need to add to state the algebraic properties of the derivative.

Theorem (Sum Rule). For any two node functions $f,g$, we have: $$(f + g)'= f' + g'.$$

Theorem (Constant Multiple Rule). For any node function $f$ and any real $c$, we have: $$(cf)' = c\, f'.$$

Theorem (Power Formula). For any positive integer $k$, we have: $$(x^{\underline {k}})'( x+h/2 )=kx^{\underline {k-1}},$$ where $$p^{\underline {q}} := p(p-h)(p-2h)(p-3h)...(p-(q-1)h). $$

Proof. From the definition, we have: $$\begin{array}{lll} (x^{\underline {k}})'( x+h/2 )&=\big( x(x-1)(x-2)...(x-k+1) \big)'\\ &=\frac{1}{h}\Big( (x+h)x(x−h)...(x−(k+2)h)−x(x−h)(x−2h)...(x−(k-2)h)(n−(k-1)h) \Big)\\ &=\frac{1}{h} x(x−h)...(x−(k-2)h)\big(x + h − (x − (k - 1)h)\big) \\ &=\frac{1}{h} khx^{\underline {k-1}}\\ &=kx^{\underline {k-1}} . \end{array}$$ $\square$

Theorem (Exponent Formula). For any positive real $b$, we have: $$(b^x)'( x+h/2 )=\frac{b^h-1}{h}b^x.$$

Exercise. Prove these theorems.

Theorem (Trig Formulas). For any real $t$, we have: $$\begin{array}{lllll} (\sin (tx))'( x+h/2 )= \frac{\sin (t\,h/2)}{h/2} \cos (t(x+h/2),\\ (\cos (tx))'( x+h/2 )=-\frac{\sin (t\,h/2)}{h/2} \sin (t(x+h/2)). \end{array}$$

Proof. We use the formulas: $$\begin{array}{lllll} \sin u - \sin v = 2 \sin\big(\tfrac{1}{2}(u-v)\big) \cos\big(\tfrac{1}{2}(u+v)\big);\\ \cos u + \cos v = -2 \sin\big(\tfrac{1}{2}(u-v)\big) \sin\big(\tfrac{1}{2}(u+v)\big). \end{array}$$ Then $$\begin{array}{lllll} (\sin tn)'( x+h/2 )&=\frac{1}{h}\Big(\sin \big(t(x+h)\big) - \sin (tx)\Big)\\ &= \frac{1}{h} 2 \sin\big(\tfrac{1}{2}t\,h\big) \cos\big(t(x+h/2)\big). \end{array}$$ $\square$

Exercise. Finish the proof.

Theorem (Product Rule). Given two node functions $f,g$, we have: $$(f \cdot g)'( x+h/2 ) = f(x+h)g'( x+h/2 ) + f'( x+h/2 )g(x).$$

Proof. $$\begin{array}{lll} (f \cdot g)'( x+h/2 )&=\frac{1}{h}\Big((f \cdot g)(x+h)- (f \cdot g)(x)\Big)\\ &=\frac{1}{h}\Big( f(x+h) \cdot g(x+h)- f(x) \cdot g(x) \Big)\\ &=\frac{1}{h}\Big( f(x+h) \cdot g(x+h)- f(x+h) \cdot g(x) +f(x+h) \cdot g(x)- f(x) \cdot g(x) \Big)\\ &=\frac{1}{h}\Big( f(x+h) \cdot g(x+h)- f(x+h) \cdot g(x) \Big)+\frac{1}{h}\Big( f(x+h) \cdot g(x)- f(x) \cdot g(x) \Big)\\ &=f(x+h) \frac{g(x+h)- g(x)}{h} +\frac{f(x+h) - f(x)}{h} g(x)\\ &=f(x+h)g'( x+h/2 ) + f'( x+h/2 )g(x). \end{array}$$ $\square$

Theorem (Quotient Rule). Given two node functions $f,g$ and any edge $[x,x+h]$, we have: $$(f/g)'( x+h/2 ) = \frac{f'( x+h/2 )g(x) - f(x+h)g'( x+h/2 )}{g(x)g(x+h)},$$ provided $g(x),g(x+h) \ne 0$.

Proof. $$\begin{array}{lll} (f / g)'( x+h/2 )&=\frac{1}{h}\Big((f / g)(x+h)- (f / g)(x)\Big)\\ &=\frac{1}{h}\Big( f(x+h) / g(x+h)- f(x) / g(x) \Big)\\ &=\frac{1}{h}\Big( f(x+h) / g(x+h)- f(x+h) / g(x) +f(x+h) / g(x)- f(x) / g(x) \Big)\\ &=\frac{1}{h}\Big( f(x+h) / g(x+h)- f(x+h) / g(x) \Big) +\frac{1}{h}\Big( f(x+h) / g(x)- f(x) / g(x) \Big)\\ &=f(x+h)\frac{1}{h}\frac{g(x)- g(x+h)}{g(x+h)g(x)} +\frac{1}{h}( f(x+h) - f(x) )\frac{1}{g(x)}\\ &=-f(x+h) \frac{g(x+h)- g(x)}{h}\frac{1}{g(x+h)g(x)} +\frac{f(x+h) - f(x)}{h} \frac{g(x+h)}{g(x)g(x+h)}\\ &=\frac{ -f(x+h)g'( x+h/2 ) + f'( x+h/2 )g(x)}{g(x)g(x+h)}. \end{array}$$ $\square$

There are no, in general, compositions of node functions and, therefore, no such rule.

Exercise. Derive the “Power Formula” for $k<0$.

Exercise. Derive the “Log Formula”: $(\log_b (tx))' ( x+h/2 )=$?

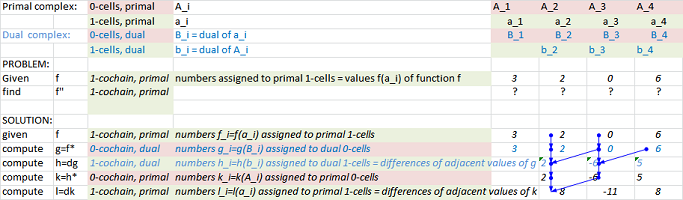
Algebraic properties of the integral

Definition. Given a primal (or dual) node function $g$. A dual (or primal) node function $g$ is called an antiderivative, or an indefinite integral, of $g$ if $f'=g$, denoted by $$f=\int g\, dx.$$

By the corollary in the last subsection, any two antiderivatives of $g$ differ by a constant.

That's why is suffices to indicate only one of them, say $$\int g(x)\, dx =f(x).$$ However, how do we present the whole, infinite collection of antiderivatives? Every antiderivative is given by the formula: $$f(x)+C,$$ where $C$ is any real number. The whole collection may look like this: $$\begin{array}{ll} ...\\ f(x)-1\\ f(x)\\ f(x)+1\\ f(x)+2\\ ... \end{array}$$ And more... The common, abbreviated way to present the collection is: $$\int g(x)\, dx =f(x)+C.$$

Example. Suppose $c$ is a real number. Let's find all the antiderivatives of the node function $f(x):=c$. From the previous experience with differentiation we recall that $$(cx)'=c.$$ Therefore, the dual node function $$g(z)=cz$$ is an antiderivative of $f$. However, to present the whole collection of antiderivatives we need to give more: $$\int c\, dx =cx+C.$$ $\square$

Below we reverse some of the computations in the last subsection.

Example. (1) $$\begin{array}{lll} F(x)=3x^2+1 & \Longrightarrow\ F'( x+h/2 )=6x+3h ;\\ f(x+h/2)=6x+3h &\Longrightarrow\ \left(\int f\, dx \right)(x)=3x^2+1. \end{array}$$ The whole collection of antiderivatives is given by $$\int (6x+3h)\, dx =3x^2 +1+C,$$ where $C$ is any real number. Since $1$ is a constant, it can be “absorbed” into $C$, as follows: $$\int (6x+3h)\, dx =3x^2 +C.$$ Also, considering the fact that $3h$ is a constant, we can modify the formula as follows: $$\int 6x\, dx =3x^2+3hx+C.$$

(2) $$\begin{array}{lll} G(x)=\frac{1}{x} &\Longrightarrow\ G'( x+h/2 )=-\frac{1}{x(x+h)};\\ g(x+h/2)=-\frac{1}{x(x+h)}&\Longrightarrow\ \left(\int g\, dx \right)(x)=\frac{1}{x}. \end{array}$$ The whole collection of antiderivatives is given by $$\int \frac{1}{x(x+h)} \, dx=-\frac{1}{x} +C.$$

(3) $$\begin{array}{lll} P(x)=2^x\ \Longrightarrow\ P'( z )=\frac{2^h-1}{h}2^{z-h/2};\\ p(x+h/2)=\frac{2^h-1}{h}2^{x} \Longrightarrow\ \left(\int p\, dx \right)(x)=2^x. \end{array}$$ The whole collection of antiderivatives is given by $$\int 2^x \, dx=\frac{h}{2^h-1}2^x +C.$$ $\square$

Some of the formulas of the derivatives in the last subsection can be easily reversed.

Theorem (Sum Rule). For any two node functions $f,g$, we have: $$\int (f + g)\, dx= \int f\, dx + \int g\, dx.$$

Theorem (Constant Multiple Rule). For any node function $f$ and any real $c$, we have: $$\int cf\, dx = c \int f\, dx.$$

We don't need the $+C$ term here because it is implicitly present in both left- and right-hand sides of the identity.

Theorem (Power Formula). For any positive integer $k$, we have: $$ \int x^{\underline {k}} \, dx = \frac{1}{k+1} x^{\underline {k+1}} +C.$$

Theorem (Exponent Formula). For any positive real $b$, we have: $$\int b^x\, dx =\frac{h}{b^h-1} b^x+C.$$

Keep in mind that in the above formulas, the left-hand sides are dual node functions. Those are functions of $z=x+h/2$. The formulas are then understood as these: $$\left( \int x^{\underline {k}} \, dx\right)(x+h/2) = \frac{1}{k+1} x^{\underline {k+1}} +C$$ and $$\left( \int b^x\, dx \right)(x+h/2)=\frac{h}{b^h-1} b^x+C.$$

Theorem (Trig Formulas). For any real $t$, we have: $$\begin{array}{lllll} \left( \int \sin (tx)\, dx \right)(z)= \frac{h/2}{\sin (t\,h/2)} \cos (tz)+C,\\ \left( \int \cos (tx)\, dx \right)(z)=-\frac{h/2}{\sin (t\,h/2)} \sin (tz)+C. \end{array}$$

Concavity and the second derivative

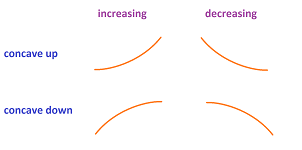
The picture below informally suggests what upward and downward concavity mean:

We can think of these as graphs of node functions zoomed out.

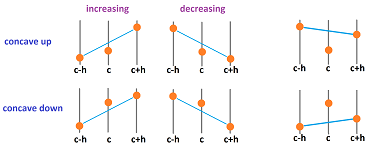
Now, let's zoom in.

The pattern is clear: it is concave up when the middle point lies below the line connecting the other two and concave down when it is above.

Definition. A node function $f$ is called concave up on interval $[a,b]$ if $$f(c)<\frac{f(c-h)+f(c+h)}{2},$$ for all adjacent edges $[c-h,c],[c,c+h]$ within the interval $[a,b]$. A node function $f$ is called concave down on interval $[a,b]$ if $$f(c)>\frac{f(c-h)+f(c+h)}{2}.$$

The sign of the differential will tell us the difference between increasing and decreasing behavior. We need a similar tool to evaluate the concavity which is a concept that captures the shape of the graph of a function in calculus as well as the acceleration in physics. The concavity is determined by the sign of the following expression: $$2f(c)-\big(f(c-h)+f(c+h)\big).$$ Let's rearrange the terms: $$=\big(f(c)-f(c-h)\big)-\big(f(c+h)-f(c)\big).$$ This is the difference of two differentials of $f$ evaluated at the two adjacent edges $[c-h,c],[c,c+h]$. To see the derivatives, let's divide this by $h^2$: $$\frac{1}{h^2}\Big(2f(c)-\big(f(c-h)+f(c+h\big)\Big) = \frac{\frac{f(c)-f(c-h)}{h}-\frac{f(c+h)-f(c)}{h}}{h}.$$

Let's take a closer look at this formula. The two fractions are recognized as the derivatives of the node function $f$ evaluated at the two adjacent edges $[c-h,c],[c,c+h]$. Then the whole expression is the rate of change of the derivative. It is the derivative of the derivative!

Definition. Given a node function its second derivative is the derivative of its derivative: $$f' '=(f')'.$$

Theorem (Concavity). (1) A node function $f$ is concave up on interval $[a,b]$ if and only if $f' '>0$ on $[a,b]$. (2) A node function $f$ is concave down on interval $[a,b]$ if and only if $f' '<0$ on $[a,b]$.

Proposition. The second derivative of a node function $g$ is a node function given by its values at each node: $$g' '(B)=\frac{1}{h^2}( dg(b) - dg(a)),$$ where $a,b$ are the edges adjacent to $B$ on the left and right respectively.

Alternatively, we have $$g' '(x)=\frac{1}{h^2}\Big( dg\big([x,x+h]) - dg\big([x,x-h]\big) \Big),$$

The duality diagram below shows the whole computation: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{lllll} \text{Primal domain: }&g' '\ ..\ g\ & \ra{d}& dg &\\ &\ua{\star} & \ne & \da{\star} & \\ \text{Dual domain: } &d(g')& \la{d} & g'& \\ \end{array} $$ Note that making the full circle won't give us the same function.

This is how the formula works:

In the pursuit of closed solutions, we will use the first derivatives computed preciosly via this formula: $$f' '(x)=\frac{f'(x+h/2)-f'(x-h/2)}{h}.$$

Example. $$\begin{array}{lll} f(x)&=3x^2+1\ \Longrightarrow\ \\ f'( x+h/2 )&=6x+3h\ \Longrightarrow\\ f' '(x)&=\frac{1}{h}\Big( (6(x+h/2)+3h)-(6(x-h/2)+3h) \Big)\\ &=6.\\ f' '(x)>0\ &\Longrightarrow\ f \text{ is concave up}. \end{array}$$

$$\begin{array}{lll}g(x)&=\frac{1}{x}\ \Longrightarrow\ \\ g'( x+h/2 )&= -\frac{1}{x(x+h)}\ \Longrightarrow\\ g' '(x)&=\frac{1}{h}\left( -\frac{1}{(x+h/2)(x+3h/2)}+\frac{1}{(x-h/2)(x+h/2)} \right)\\ &=\frac{1}{h}\frac{1}{x+h/2}\left( -\frac{1}{x+3h/2}+\frac{1}{x-h/2} \right)\\ &=\frac{1}{h}\frac{1}{x+h/2} \frac{-(x-h/2)+(x+3h/2)}{(x+3h/2)(x-h/2)}\\ &=\frac{2}{(x-h/2)(x+h/2)(x+3h/2)}.\\ g' '(x)<0 \text{ for } x\le -1 &\Longrightarrow\ g \text{ is concave down on } (-\infty,-1];\\ g' '(x)>0 \text{ for } x\ge 1 &\Longrightarrow\ g \text{ is concave upon } [1,\infty]. \end{array}$$

$$\begin{array}{lll} h(x)&=2^x\ \Longrightarrow\ \\ h'( x+h/2 )&= \frac{2^h-1}{h}2^x \ \Longrightarrow\ \\ h' '(x)&=\frac{1}{h}\Big( \frac{2^h-1}{h}2^{x+h/2} - \frac{2^h-1}{h}2^{x-h/2} \Big)\\ &=\frac{1}{h} \frac{2^h-1}{h} 2^{x} ( 2^{h/2} - 2^{-h/2})\\ &=\left( \frac{2^h-1}{h} \right)^2 2^{-h} 2^{x}. \\ h' '(x)>0\ &\Longrightarrow\ h \text{ is concave up}. \end{array}$$

With just this data (and the increasing/decreasing behavior established earlier) we can sketch the graphs of these three functions:

$\square$

The second derivative is computed with a spreadsheet:

Link to file: Spreadsheets.

Newton's Laws

The concepts introduced above allow us to state some elementary facts about the discrete Newtonian physics, in dimension $1$.

First, the time is given by the standard domain, the discrete representation of ${\bf R}$. Second, the space is given by ${\bf R}$, at the simplest.

The main quantities we are to study are:

• the location $r$ is a primal node function;
• the displacement $dr$ is a primal edge function;
• the velocity $v=r'$ is a dual node function;
• the momentum $p=mv$, where $m$ is a constant mass, is also a dual node function;
• the impulse $J=dp$ is a dual edge function;
• the acceleration $a=r' '$ is a primal node function.

Some of these discrete functions are seen in the following duality diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{lllll} \text{Primal domain: }&a\ ..\ r\ & \ra{d}& dr &\\ &\ua{\star} & \ne & \da{\star} & \\ \text{Dual domain: } &J/m& \la{d} & v& \\ \end{array} $$ Note that making the full circle won't give us the location function.

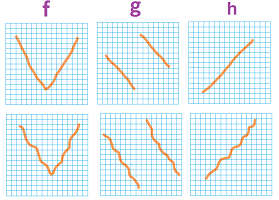
For example, the upward concavity of the discrete function below is obvious, which indicates a positive acceleration:

Newton's First Law: If the net force is zero, then the velocity $v$ of the object is constant: $$F=0 \Longrightarrow v=const.$$

The law can be restated without invoking the geometry of time:

• If the net force is zero, then the displacement $dr$ of the object is constant:

$$F=0 \Longrightarrow dr=const.$$ The law shows that the only possible type of motion in this force-less and distance-less space-time is uniform; i.e., it is a repeated addition: $$r(t+1)=r(t)+c.$$

Newton's Second Law: The net force on an object is equal to the derivative of its momentum $p$: $$F=p'.$$

As we have seen, the second derivative is meaningless without specifying geometry, the geometry of time.

Newton's Third Law: If one object exerts a force $F_1$ on another object, the latter simultaneously exerts a force $F_2$ on the former, and the two forces are exactly opposite: $$F_1 = -F_2.$$

Law of Conservation of Momentum: In a system of objects that is “closed”; i.e.,

• there is no exchange of matter with its surroundings, and
• there are no external forces; $\\$

the total momentum is constant: $$p=const.$$

In other words, $$J=dp=0.$$ To prove, consider two particles interacting with each other. By the third law, the forces between them are exactly opposite: $$F_1=-F_2.$$ Due to the second law, we conclude that $$p_1'=-p_2',$$ or $$(p_1+p_2)'=0.$$

Exercise. State the equation of motion for a variable-mass system (such as a rocket). Hint: apply the second law to the entire, constant-mass system.

Exercise. Create a spreadsheet for all of these quantities.

To study physics in dimension $3$, one simply combines three discrete functions for each of the above quantities: $$f_i:{\mathbb R}\to {\bf R},\ i=1,2,3,$$ into one: $$f=(f_1,f_2,f_3):{\mathbb R}\to {\bf R}^3.$$