Find the point of the graph nearest to 0

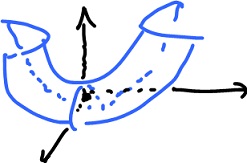
Find the points on the surface

 z = 2xy + 1 / 4

nearest to the origin.

Review exercise. Find the points on the curve

 f(x) = x2 + 2x + 2

to the 0. Now find the partial derivatives:

 ∂f / dx = 2y = 0,  ∂d / dy = 2x = 0,

solving

 x = 0, y = 0 and z = 1 / 4,

and hence

 the point nearest to the origin is ( 0, 0, 1 / 4 ).

Continue. Find the points on the surface

 z = 2xy + 1 / 4

nearest to the origin. Note that this is different from finding the minimum of

 z = f( x, y ) = 2xy + 1 / 4.

Q: Point ( x, y, z ), distance to the 0-point is

 g( x, y, z ) = x2 + y2 + z2,

where z = 2xy + 1 / 4. Then minimize

 h( x, y ) = x2 + y2 + ( 2xy + 1 / 4 )2,

i.e. the square of the distance of a point ( x, y, z ) on the surface to 0.

Solution:

 h( x, y ) = x2 + y2 + 4 x2 y2 + xy + 1 / 16.

Then

 ∂h / ∂x = 2x + 8xy2 + y = 0,
 ∂h / ∂y = 2y + 8x2y + x = 0,

hence

 x = 0, y = 0. (Why?)

Find all x, y satisfying the system

 2x2 + 8x2y2 + xy = 0
 2y2 + 8x2y2 + xy = 0
 ----------------------
 2x2 - 2y2 = 0

hence

 x = ± y.

Substitute back ( x = y ):

 2x + 8x3 + x = 0
 8x3 + 3x = 0
 x ( 8x2 + 3 ) = 0,
 x = 0 → y = 0.
 
 (1) → x = -y / ( 2 + 8 y2 )
 (2) 2 y + y2 / ( 2 + 8y2 )2 + ( -y ) / ( 2+ 8y2 ) = 0

Exercise. Let

 y = x2 - a.

Find the nearest point to 0.

 d(x) = x2 + y2
      = x2 + x4 - 2ax2 + a2,

 d′(x) = 2x + 4x3 - 4ax = x ( 2 - 4a + 4x2 ) = 0
 → x = 0 or 2 - 4a + 4x2 = 0,

hence

 x = 0 or x = ± ( a - 1 / 2 )1/2 ∈ ℝ if a > 1 / 2:
 Case 1: -( a - 1 / 2 )1/2 -( a - 1 / 2 )1/2 if a > 1 / 2,
 Case 2: if a ≤ 1 / 2
 If a = 1 / 2, d′(x) = x3.

As a passes through 1/2, one solution (which is also the minimum of f) becomes two solutions (bifurcation).