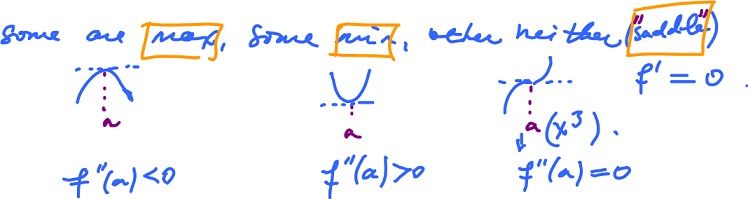Extrema of functions of several variables

Introduction

Let's review how we handle extrema of functions of one variable, from Calc 1.

Let $y = f(x)$. To find the local maximum or minimum, proceed as follows:

• compute $f'(x)$,
• solve $f'(x)$ $= 0$ for $x$, (also find $x$'s for which $f'(x)$ does not exist)
• these are the critical points of $f$.
• some of these are maxima, some are minima, others are neither (in this case, they will be called "saddles").
• second derivative test: classify the critical points based on the sign of $f' '(a)$. Note that it is possible that $a$ is a minimum and $f' '(a) = 0$. Example: $y = x^4 at a = 0$.
• first derivative test: classify the critical points based on change of the sign of $f'(a)$

$$f'(x) > 0 {\rm \hspace{3pt} for \hspace{3pt}} x < a {\rm \hspace{3pt} and \hspace{3pt}} f'(x) < 0 {\rm \hspace{3pt} for \hspace{3pt}} x > a,$$

$$f'(x) < 0 {\rm \hspace{3pt} for \hspace{3pt}} x < a {\rm \hspace{3pt} and \hspace{3pt}} f'(x) > 0 {\rm \hspace{3pt} for \hspace{3pt}} x > a,$$

no change.

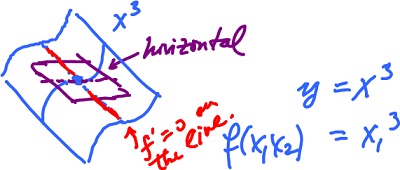
In the $n$-dim case, the tangent lines are replaced with tangent planes, or, more precisely, tangent hyperplanes. Those are horizontal at the extreme points,

• $f'(a)$ $= 0$ ($0$ vector), or
• ${\nabla}f(a)$ $= 0$ ($0$ linear operator), or
• $\frac{\partial f}{\partial x}_i (a)$ $= 0$ for $i = 1, ..., n$ (numbers).

Example. Consider $f(x,y) = x^3$.

There are infinitely many directions to follow in the $d$-dim case, but the definition of extreme points is the same.

Definition. Point $a$ is called a global maximum of $f: {\bf R}^n {\rightarrow} {\bf R}$ if

$f(x) \leq f(a) {\rm \hspace{3pt} for \hspace{3pt} all \hspace{3pt}} x {\in}$ $D(f)$.

Analogously, $a$ is called a global minimum of $f(x)$ if

$$f(x) \geq f(a) {\rm \hspace{3pt} for \hspace{3pt} all \hspace{3pt}} x {\in} D(f).$$

Is it well defined?

• may not always exists (affine function) and
• may not always be unique (periodic function).

Definition. Suppose $a$ is an interior point of $D(f)$. Then $a$ is a local maximum point of $z = f(x)$ if

$$f(x) \leq f(a)$$

for all $x$ in an open ball around $a$ (i.e. there is an $\epsilon > 0$ such that for $|| x - a || < ε$ follows that $f(x) \leq f(a))$.

Analogously we define a local minimum point. Extreme points are minima or maxima, both local and global.

Using the gradient

The gradient is used to find the extreme point of a function of several variable in a manner similar to the $1$ dim case.

Theorem (First derivative test). Suppose $a$ is a local extreme point of a differentiable function $f$. Then

1. $f'(a) = 0,$
2. ${\nabla}f(a) = 0,$
3. $\frac{\partial f}{\partial x}_i (a) = 0$ for all $i = 1, ..., n$.

Exercise. Let $f( x_1, x_2 ) = x_1^2 + x_2^2$. Find the extrema.

Solve the equations:

$$\frac{\partial f}{\partial x}_1 = 2x_1 = 0 \rightarrow x_1 = 0,$$

$$\frac{\partial f}{\partial x}_2 = 2x_2 = 0 \rightarrow x_2 = 0.$$

Hence the point $( 0, 0 )$ is the only critical point of f (minimum).

Exercise. Let

$$g( x_1, x_2 ) = x_1^2 - x_2^2. $$

Then the calculation is the same as above, and we obtain $( 0, 0 )$ as the only critical point (saddle).

Exercise. Let

$$f = ( x_1, x_2 ) = x_1^2.$$

Then

$$\frac{\partial f}{\partial x}_1 = 2x_1 = 0 \rightarrow x_1 = 0,$$

$$\frac{\partial f}{\partial x}_2 = 0.$$

Hence the critical points are

$$\{ ( 0, x_2 ) : x_2 {\in} ℝ \},$$

which form a line.

Proof of the theorem. Suppose the point $a$ is a maximum for $f: {\bf R}^n {\rightarrow} {\bf R}$. Suppose $a = ( a_1, ..., a_n )$.

Consider

$$f_1: {\bf R} {\rightarrow} {\bf R}, f_1(x) = f( x_1, a_2, ..., a_n ),$$

which is differentiable. Then $x = a_1$ is a max of $f_1$. Now, by the First Derivative Test from Calc 1, we have

$$f_1'( a_1 ) = 0.$$

This derivative is equal to the partial derivative:

$$\frac{\partial f}{\partial x}_1 (a) = 0.$$

Continue with $f_k: {\bf R} {\rightarrow} {\bf R}$,

$$f_k(x) = f( a_1 ... a_{k-1} \times a_{k+1} ... a_n). $$

Then $f_k$ is differentiable, and $x = a_k$ is a maximum. Find

$$f'_k (a_k) = 0, $$

so

$$\frac{\partial f}{\partial x}_k (a) = 0.$$

Thus all partial derivatives of $f$ are equal to $0$. Hence the gradient is zero too:

${\nabla}f(a) = 0$ (a vector),

so

$f'(a) = 0$ (a linear map). QED

Exercise. Without using the First Derivative Test from from Calc. 1, show that the directional derivative is $0$,

${\nabla}_e f(a) = 0$ for all $e$.

The first derivative $f'(a)$ is a linear map for all $a$. In this sense $f'(a)(u)$ is a function in two variables, linear with respect to $u$.

The second derivative $f' '(a) = ( f'(a) )'$ is a quadratic map for all $a$. In this sense, $f' '(a)(u)$ is a function in two variables, $u$ quadratic.

Global extrema

Given $f: {\bf R} {\rightarrow} {\bf R}$. Find the global maximum / minimum with $x {\in} [ a, b ]$ (which is a constraint). First, does it always exist?

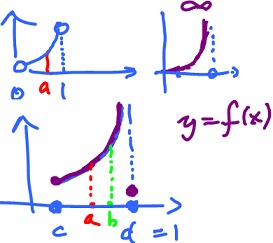
Example. (1) Let $f(x) = x^2$. The maximum on the interval $( 0, 1 )$ does not exist. Indeed by definition, a is a maximum point if

$$f(a) \geq f(x) {\rm \hspace{3pt} for \hspace{3pt} all \hspace{3pt}} x {\in} ( 0, 1 ). $$

Now suppose there is such an $a {\in} ( 0, 1 )$, but we can always find another value $b$ such that $f(b) > f(a)$ (contradiction): Choose

$$b = a + \epsilon, {\rm \hspace{3pt} with \hspace{3pt}} \epsilon = \frac{1 - a}{2}$$

or

$$b = \frac{a + 1}{2}.$$

Now show that if $a < 1$, then $( a + 1 ) < 1$. Then show that $f( \frac{a + 1}{2} ) > f(a)$.

So, to guarantee the existence of the maximum we have to require that $x$ runs through $[ a, b ]$, i.e. a closed interval (with the end points included).

What if $x {\in} [ a, {\infty} )$? Suppose $a$ is a maximum, let $b = a + 1$. So, to guarantee the existence of the maximum we have to require $x {\in} [ a, b ]$, i.e. that the interval is bounded.

Exercise. What if $f$ is not continuous? Let $f: [ r, d ] {\rightarrow} {\bf R}$. By contradiction prove that there is no maximum:

$$f(a) < f( \frac{a + 1}{2} ).$$

From Calc 1,

Theorem. A continuous function $f: [ a, b ] {\rightarrow} {\bf R}$ attains its maximum or minimum on a closed bounded interval.

Similarly,

Theorem. A continuous function $f: Q {\rightarrow} {\bf R}, Q ⊂ {\bf R}^n$, attains its maximum or minimum on a closed bounded subset $Q ⊂ {\bf R}^n$.

Topology background

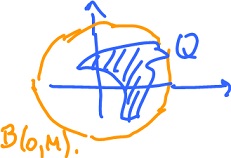
Definition. A subset $Q ⊂ {\bf R}^n$ of ${\bf R}^n$ is bounded if there is $M {\in} {\bf R}$ such that

$$|| x || \leq M {\rm \hspace{3pt} for \hspace{3pt} all \hspace{3pt}} x {\in} Q$$

or

$Q \subset$ $B( 0, M )$.

On an unbounded set, the value of $f$ might approach ${\infty}$. In this case, there is no maximum. If the endpoint of an interval is not included in $Q$ (constraint), $f {\rightarrow} {\infty}$, possibly, even if $f$ is continuous.

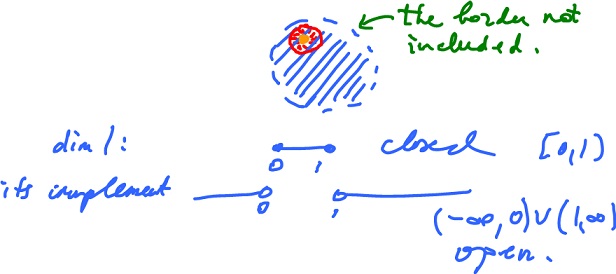
Definition. A subset $Q \subset {\bf R}^n$ of ${\bf R}^n$ is open if every point in $Q$ is an interior point.

Definition. A subset $Q \subset {\bf R}^n$ of ${\bf R}^n$ is closed if its complement is open.

For more see Open and closed sets.

Proposition. A closed ball

$$\{ x {\in} {\bf R}^n: || x || \leq R \}$$

is closed. Analogously, an open ball

$$\{ x {\in} ℝ^n: || x || < R \}$$

is open.

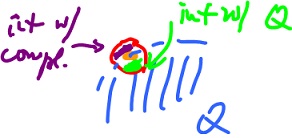
Definition. A point $a {\in} Q$ is a boundary point of $Q$ if every ball around a intersects both $Q$ and the complement of $Q$.

Proposition. If $Q$ is closed, then $Q$ contains all of its boundary points.

Theorem. A continuous function $f: Q {\rightarrow} {\bf R}$ attains its maximum or minimum values on a closed bounded subset of ${\bf R}^n$.

How to find extrema

Now we know when the existence of a global max.min is guaranteed, we can devise a plan:

Algorithm. Suppose f is differentiable.

1. Find all critical points of $f$ via the equation $f'(a) = 0$,
2. add the end points.
3. Compare the values.

Exercise. Let $f: {\bf R}^2 {\rightarrow} {\bf R}$. Does it attain its minimum or maximum if $f( x, y ) = x^2 + y^2$?

Another exercise: Find the point of the graph nearest to $0$.

Review exercise. (a) Compute the derivative of $f: {\bf R}^n {\rightarrow} {\bf R}, f(x) = || x ||$, at $a \neq 0$,

(b) Compute the derivative of $h: {\bf R}^n {\rightarrow} {\bf R}, h(x) = sin || x ||$, at $a \neq 0$ (hint: use part (a)).