Elections

Social choice: ranking

Let's observe that by requiring the vote to be a meaningful (i.e., transitive, non-circular) ranking we make the topology of the space of outcomes topologically non-trivial, non-acyclic. As we already demonstrated, the non-triviality of the topology can make impossible some of the aggregation schemes of social choice. Is there an alternative?

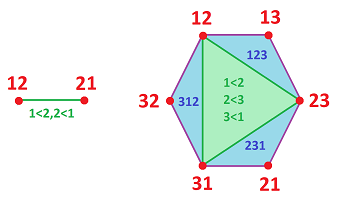
We can simply include the “impossible” ballots, such as this: $1<2, 2<1$, etc. What difference does it make? For $n=2$, we have now: $$U_{12}\cap U_{21} \ne \emptyset .$$ Therefore, the nerve of this cover will contain an edge between these two vertices. Then the space of choices becomes acyclic!

In general, a valid ballot (an element of $Z$) is a complete, acyclic directed graph on the set of $n$ vertices/candidates. Let's drop both of these restrictions:

• a ballot is a directed graph on the set of $n$ vertices.

The open cover $\alpha$ is still the collection of $U_{ij}$ but this time there are no empty intersections. Therefore, the space of all ballots $N_{\alpha}$ is a simplex!

Exercise. What is the dimension of this simplex?

What if next we want to go in the opposite direction and to extend a map from higher dimensional simplices to the vertices and the rest?

Given a simplicial complex $K$, suppose $\sigma$ is one of its simplices and $\dim \sigma =n$. Then $\sigma$ is called a maximal simplex if it is not a boundary simplex of any $(n+1)$-simplex.

Let $M(K)$ stand for the set of maximal simplices of complex $K$.

Corollary. If $g:K\to L$ is a simplicial map then $$g(A)\in\bigcap\{ g(s):\ s\in \operatorname{St}_{M(K)}(A) \}.$$

Then the non-emptiness of this set is a necessary condition for existence of an extension of $g$ from $M(K)$ to $K$. We will demonstrate later that this is also a sufficient condition.

Exercise. Prove the corollary.

ratings iii

• Independence. (Independence of irrelevant alternatives) If no voter has changed his vote for a given candidate (or a pair) from the election to the next, then the tallied vote for the candidate hasn't changed either:

$$\forall a \in C_0,\ \forall X,Y \in (C^0)^m,$$ $$X_i(a)=Y_i(a) \Rightarrow f(X)(a)=f(Y)(a).$$

Proposition. The sum tally $\Sigma$ satisfies Independence.

Then, another way to express this axiom is as follows. Each candidate $a$ is evaluated separately within each of the elections $X$. In our algebraic setting, the axiom is equivalent to a more compact version:

• $f(X)(a)$ depends only on $X\delta (a)$.

Theorem. A rating tally satisfies Independence if and only if there is such a homomorphism $f':R^m\to R$ that we have: $$f(X)(a)=f'X\delta (a).$$

In other words, the following composition represents both sides: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{ccccccc} C_0 & \ra{\delta} & (C_0)^m & \ra{X} & R^m & \ra{f'} & R . \end{array}$$

Exercise. Prove the theorem. Hint: does $f'$ have to be a homomorphism?

Note: If we normalize the tallied votes, the result will be a lottery on $K$. Running an actual lottery can then be used to determine the winner.

Graded tallies

Now, what if votes of two or more degrees are cast? These votes are then processed by a collection of tallies, such as: $$f^k:(C^k)^m \to C^k,\ k=0,1,2,...,$$ one for each degree.

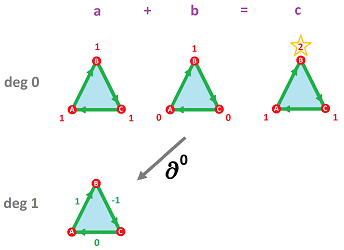
Proposition. Elections form a cochain complex $\{(C^k)^m,D\}$, where $$D(x_1, ..., x_m):=(\partial^*x_1, ..., \partial^*x_m).$$

Proof. $$DD(x_1, ..., x_m):=(\partial^*\partial^*x_1, ..., \partial^*\partial^*x_m)=(0,...,0).$$ $\blacksquare$

Exercise. Demonstrate, however, that this cochain complex isn't the same as $C^*(K^m)$ or $(C^*(K))^m$.

Now, if we have a graded tally $$f:(C^k)^m \to C^k,\ k=0,1,2,...,$$ is it a cochain map? This diagram has to commute: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccc} (C^1)^m & \ra{f^1} & C ^{1} \\ \ua{D^0} & & \ua{\partial^0}\\ (C^0)^m & \ra{f^0} & C ^{0} \end{array} $$

Proposition. The graded sum tally $\Sigma ^i:(C^i)^m \to C^i,\ i=0,1,$ is a cochain map.

Proof. Let $X=(X_1,...,X_m)\in (C^0)^m$. Let's trace the diagram in both directions. First, $$\Sigma ^0(X)=X_1+...+X_m,$$ then $$\begin{array}{lll} (\partial^0\Sigma^0X)(AB)&=(X_1+...+X_m)(B)-(X_1+...+X_m)(A)\\ &=(X_1(B)+...+X_m)(B))-(X_1(A)+...+X_m(A)). \end{array}$$ Second, $$\Sigma^1(D^0X)=\partial^0X_1+...+\partial^0X_m,$$ then $$\begin{array}{lll} (\Sigma^1D^0X)(AB)&=\partial^0X_1(AB)+...+\partial^0X_m(AB)\\ &=(X_1(B)-X_1(A))+...+(X_1(B)-X_1(A)). \end{array}$$ $\blacksquare$

Should all graded tallies be cochain maps?

Suppose, hypothetically, that a comparison election and a rating election are run in parallel on the same day. Suppose every voter casts his vote in both but this time he doesn't change his mind so that his two votes match. Then the outcome votes of the two elections should match too.

We introduce a new axiom.

• Algebraic continuity. Graded tally $\{f^0,f^1\}$ is a cochain map:

$$\partial^0f^0(X_1,...,X_m)=f^1(\partial^0X_1,...,\partial^0X_m).$$

Since we can't simply set $f^1=0$, the axiom is meaningful even when there are no comparison votes.

Rankings and preferences

Real-life electoral systems often rely on rankings of candidates. Since ranking votes lack the algebra described above, they deserve a separate treatment. Another example of number-less comparison is pairwise preferences. We put both under the umbrella of sorting.

We still have $n$ ordered alternatives: $$\{0,1,2,...,n-1\}=\{A_0,A_1, A_2, ... ,A_{n-1}\},$$ as the vertices of a connected graph $K$.

The definitions below are parallel to the ones about algebraic votes presented in the last subsection.

Definition. A ranking, or a ranking vote, is a strict ordering with possible ties of the candidates

For example, we may have: $$A_0=A_1< A_2< ... =A_{n-1}.$$ In other words, this is a list that can have several candidates per item. As an ordering, its pairwise order relation is transitive: $A < B < C \Rightarrow A < C$, and, of course, $A= B= C\Rightarrow A= C$. Rankings will also be referred to as sortings of degree $0$ and their totality is denoted by $S^0(K)$.

Note: Ties are allowed but we will avoid using non-strict inequalities, $A\le B$, for candidates as they don't clearly show who won.

For an algebraic representation of rankings, we will use the set of all finite non-decreasing strings of $n$ positive integers: $$L_n:= \{(X_0,...,X_{n-1}): X_i\in {\bf Z}^+,\ X_0\le X_1\le ... \le X_{n-1}\}.$$ We will use the function $$\epsilon_0:S^0(K) \to L_n,$$ defined by $$\epsilon _0(X):=(X_0,...,X_{n-1}),$$ where $X_i$ is the position of candidate $i$ in the list $X$, or $$X(i)=X_i.$$

Exercise. Use this algebra to interpret: $"<" \ + ">" \ = \ "="$.

Definition. A preference, or a preference vote, is a pairwise ordering of the candidates, within $K$.

For example, we may have: $$A_0=A_1,A_0< A_2,A_1<A_2, ... ,A_n=A_{n-1}.$$ In other words, we give a sign, one of the three: $$< \ = \ >$$ to each pair of comparable candidates, i.e., to the edge in $K$ that connects them. As the signs are given to all edges, a preference is simply a directed, with ties, graph on $K$. Preferences will also be referred to as sortings of degree $1$ and their totality is denoted by $S^1(K)$.

Note: In contrast to a set of preferences considered previously, lotteries (mixed strategies) aren't allowed.

For an algebraic representation of preferences, we will use the set of signs and the function of signs: $$sign:\{<,=,>\} \to \{-1,0,1\}.$$ We suppose that there are $M$ edges of $K$ and they are ordered. We use the function $$\epsilon_1:S^1(K) \to \{-1,0,1\}^M,$$ defined by $$\epsilon _1(x_1,...,x_M):=(sign(x_1),...,sign(x_M)),$$ where $x_i$ is the sign given to $i$th edge of $K$.

Similar to the relation between a $0$-chain and a $1$-chains (as well as a set of preferences and its utility) is the following. Each ranking vote $X$ produces a preference vote $x$, as follows: $$X(1)< X(2) \Rightarrow 1 < _x 2.$$ This map: $$\partial^0:S^0(K)\to S^1(K).$$ is the analogue of the coboundary operator. Algebraically, we have $$\partial ^0(X)(12):=sign^{-1}(\epsilon_0(X(2))-\epsilon_0(X(1))).$$

Exercise. Define $S^2(K)$ and $\partial ^1$.

The preference vote that has only $=$ present is denoted by $0$. It is represented by $\epsilon^1(0)=(0,0,...,0)$.

A ranking preference vote is one that comes from some ranking vote of the candidates, as described above: $x=\partial^0(X)$. Therefore, it's the analogue of a $1$-coboundary.

A non-circular preference vote is one the directed graph of which has no cycles other than fully tied. Therefore, this is the analogue of a $1$-cocycle.

Exercise. Show that the fully tied ranking vote $T=\{1=2=3=...\}=(\epsilon^0)^{-1}(T)=(1,1,...,1)$ is the only one that satisfies $\partial ^0(T)=0$.

The relation between the new concepts parallels the old as shown below: $$\newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{ccccccc} C^0(K) & \ra{\partial^{0}} & C^1(K) & \\ \downarrow ^{p^0} & & \downarrow ^{p^1} & \\ S^0(K) & \ra{\partial^{0}} & S^1(K) \end{array}$$

More than just an analogy, we would like to establish a direct link between the algebraic votes and the sorting votes. Then, the former are numbers that have to be subject to an order relation. That's why we choose the ring of coefficients $R$ to be either ${\bf R}$ or ${\bf Z}$.

It is then easy to define the functions for the down arrows in this diagram.

• The numbers assigned by $r\in C^0(K;R)$ to the vertices of $K$ create an ordering of these vertices; that's $p^0(r)\in S^0(K)$.
• The numbers assigned by $c\in C^1(K;R)$ to the edges of $K$ create a relation ($<$, $>$, or $=$) between each pair of adjacent vertices; that's $p^1(c)\in S^1(K)$.

Exercise. Prove that the diagram is commutative.

Exercise. Interpret the relation between $C^0,C^1$ and $S^0,S^1$ as (a) an equivalence relation, (b) a functor. Hint: it's somewhat forgetful.

Exercise. Describe the left or right inverses of $p^0$ and $p^1$.

We continue with the parallel theory.

Proposition. Every ranking preference vote is non-circular.

Proposition. If $K$ is a tree, every preference vote is ranking.

Exercise. Prove the propositions.

A stronger statement is the following.

Theorem (Topological Sorting). Every non-circular preference vote is ranking.

Proof. Let's assume that the vote is given by an acyclic directed graph $G$ with no ties. Then it allows a “topological sorting”: $$AB\in G \Leftrightarrow A < B.$$ The sorting is built by a recursive process as follows:

• (1) Start with a source $s$ and add it to top of the list.
• (2) Remove $s$ and all outgoing edges of $s$ from $G$.
• (3) Repeat.

$\blacksquare$

Exercise. (a) Prove the theorem for the general case (with ties). (b) What is the relation of the theorem to the last proposition?

Even in the case of a single voter, who wins?

In the simplest case, there are no preference votes. Then we choose the winner to be the one (possibly tied) with the highest ranking given by the voter.

What if the voter casts a preference vote $b$ instead? Even though what we really need is a ranking vote, we don't have to discard $b$. The reason is that $b$ may be a ranking preference vote: $b=\partial^0(c)$ for some rating $c$ (i.e., $b$ is a coboundary). Then the winner should be the one with the largest value of $c$. We conclude that

• we can guarantee that there is such a $c$ when $K$ is a tree or when $c$ is non-circular; then
• the choice of the winner(s) is unambiguous.

Exercise. Prove the second statement.

Unlike algebraic votes, sorting votes can't be simply added together as a way to find the total vote of an election. The issue is discussed later.

Social choice: higher order voting

Recall that we previously considered $n$ alternatives/candidates, $$\{0,1,2,...,n-1\}=\{A,B,C,...\},$$ placed at the vertices of a simplicial complex $K$. Then the $1$-cochains over $R={\bf R}$ or ${\bf Z}$ are the pairwise comparisons of the candidates.

What about the higher degree cochains? Do they have meaningful interpretations as votes?

Let's start with the fact that it is the inability of the voter to assign a number to each single candidate to convey his perceived value (or quality or utility or rating) what makes degree $1$ (comparison) votes necessary. Similarly, the inability of the voter to assign a number to each pair of candidates to convey their relative value is what makes comparison of triples necessary.

Let's consider some examples.

On the most basic level, voters compare alternatives to, say, $0$. For example, voter may judge:

• candidate $A$ is worth $1$.

Translated:

• $a(A)=1.$

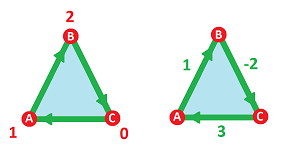
Here, a $0$-chain $A$ is evaluated by a $0$-cochain $a$.

On the next level, voters compare the alternatives (i.e., the vertices of $K$) to each other. For example, the voter may judge:

• candidate $A$ is worse, by $1$, than candidate $B$.

Translated:

• $a(B)-a(A)=1.$

What do we do with this vote? This comparison vote may have come from a rating but there are many possibilities: $$a(A)=0,a(B)=1\ \text{ or } a(A)=1,a(B)=2\ \text{ etc.}$$ In addition, this comparison vote might conflict with others; for example, the total vote may be circular: $$a(B)-a(A)=1,\ a(C)-a(B)=1,\ a(A)-a(C)=1.$$ We don't try to sort this out; instead, we create a single pairwise comparison:

• $b(AB):=1.$

Here, a $1$-chain $AB$ is evaluated by a $1$-cochain $b$.

In the case of three candidates, there are $3$ of $0$-degree votes and $3$ of $1$-degree votes:

Exercise. Analyze in this fashion the game of rock-paper-scissors.

The voter may compare chains as linear combinations of the alternatives; for example, “the average of candidates $A$ and $B$”. Of course, we understand this chain as the 50-50 lottery between $A$ and $B$.

Exercise. Represent the following vote as a cochain:

• the average of candidates $A$ and $B$ is worse, by $B$, than candidate $C$.

On the next level, the voter may express himself in terms of comparisons of comparisons. For example, the voter may judge:

• the combination of the advantages of candidate $B$ over $A$, $C$ over $B$, and $C$ over $A$ is $1$.

Translated:

• $b(AB)+b(BC)+b(CA)=1$.

We simply create a single triple-wise comparison:

• $c(ABC):=1.$

Here, a $2$-chain $ABC$ is evaluated by a $2$-cochain $c$.

Exercise. Show that the triple vote above (a) may come from a variety of pairwise comparisons and (b) may be in conflict with other votes.

Let's sum up. These are possible votes:

• Candidate $A_0$ is evaluated by a vote of degree $0$: $a^0\in C^0$ and $a^0(A_0)\in R$.
• Candidates $A_0$ and $A_1$ are evaluated by a vote of degree $1$: $a^1\in C^1$ and $a^1(A_0A_1)\in R$.
• Candidates $A_0$, $A_1$, and $A_2$ are evaluated by a vote of degree $2$: $a^2\in C^2$ and $a^2(A_0A_1A_2)\in R$.
• ...
• Candidates $A_0$, $A_1$, ... $A_k$ are evaluated by a vote of degree $k$: $a^k\in C^k$ and $a^k(A_0A_1...A_k)\in R$.

Definition. A vote is any cochain in complex $K$: $$a=a^0+a^1+a^2+...,\ a^i\in C^i(K).$$

Now, how do we make sense of the outcome of such a vote? Who won?

In the simplest case we ignore the higher order votes, $a^1,a^2,...$, and choose the winner to be the one with the highest rating: $$winner:=\arg\max _{i\in K^{(0)}} a^0(i).$$

When $a^1$ isn't constant, what do we do with this information about pairwise comparisons? Do we have to discard it? Not necessarily: if $a^1$ is a rating comparison vote (i.e., a coboundary), we can use it to create a new set of ratings: $$b^0:=(\partial^0)^{-1}(a^1).$$ We then find the candidate(s) with the highest value of $$c^0:=a^0+b^0$$ to become the winner.

Example. Suppose $a^0=1$ and $$a^1(AB)=1,\ a^1(BC)=-1,\ a^1(CA)=0.$$ We choose: $$b^0(A)=0,\ b^0(B)=1,\ b^0(C)=0,$$ and observe that $$\partial^0 b^0=a^1.$$ Therefore, $B$ is the winner!

$\square$

Thus the comparison vote helps to break the tie.

Exercise. Show that such a winner (or winners) is well-defined.

Exercise. Show that the definition applies only when $K^{(1)}$ is a tree.

Exercise. (a) Give other examples of how $a^1$ helps determine the winner when $a^0=0$. (b) Can $a^2$ help determine the winner when $a^0=0, a^1=0$?

Social choice: elections

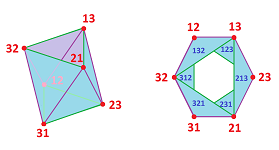
As before we suppose the number $n$ of alternatives/candidates is fixed: $$A_n:=\{1,2,...,n\}=\{C_1, C_2, ... ,C_n\}.$$ Let's review first what a single voter does. Voter $x$'s vote is a (strict) ordering of the alternatives: $$C_1 <_x C_2 <_x \ ... <_x C_n \quad \leadsto \quad x=(C_1,C_2 , ... ,C_n).$$ The totality of all possible votes/voters is the set of these orderings: $$Z_n:=\{(C_1,C_2 , ... ,C_n):\ C_k\in A_n,C_k\ne C_l\}.$$ For each two candidates $i,j$, the sets $$U_{ij}:=\{ x\in Z_n: i<_xj \},$$ form an open cover of $Z_n$, the nerve $R_n$ of which is the complex of orderings (or rankings).

To sum up what we know about $R_n$:

• (1) The vertices of $R_n$ correspond to the pairwise preferences $U_{ij}$ over $A_n$.
• (2) The $N$-simplices, where $N:=\dim Z$, of $R_n$ correspond to the orderings of $A_n$, i.e., the elements of $Z_n$.
• (3) $|R_n|$ is the union of these simplices.

Now the elections.

Suppose we have $m$ voters: $$V=V_m:=\{1,2,...,m\}.$$ Then an election is any combination of $m$ votes and the set of all possible elections is the product, $Z_n^m$.

However, what we will deal with instead is the $m$th power of the complex of orderings $R_n^m$ as a complex that records all possible elections. This is not a simplicial complex but a cell complex with cells given as products $$s=x_1 \times ... \times x_m$$ of some $N$-simplices $x_1, ..., x_m \in Z_n$.

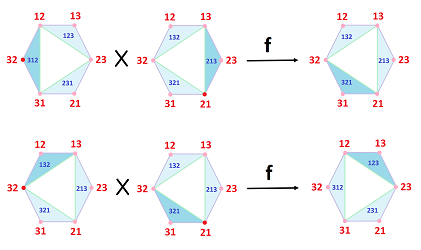
Example. For $n=3$, $$Z_3=\{123,132,231,321,213,312\}.$$ This may be an example of an election for $m=4$:

$\square$

Who won? An election rule $$f: Z_n^m \to Z_n$$ converts any election, an element of $Z_n^m$, into a single vote, an element of $Z_n$: $$r=f(X)=f(x_1, ..., x_m).$$ Therefore outcome takes the same form, an ordering of the candidates: $$C_1 <_r C_2 <_r C_3 <_r \ ... <_r C_n.$$

For now, we will ignore the issue of whether this rule is fair. Instead, let's just make sure it makes sense mathematically.

Is $f$ a simplicial map? It is only a correspondence:

• $f$ takes each $Nm$-cell of $Z^m$ to an $N$-cell of $Z$.

Can we construct a simplicial map from $f$ by extending this correspondence to the rest of the cells of $Z^m$?

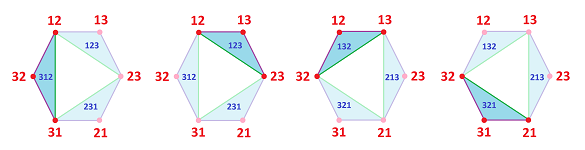
Example. For $n=3$ and $m=2$, this may be an example of two elections and their outcomes:

Here: $$f(312 \times 213)=321,\ f(132 \times 321)=123.$$ Now, we can't find a value for vertex $(32,21)$ because the values of $f$ on the two cells that contain it don't intersect. Therefore, such a simplicial map is impossible!

$\square$

This analysis is confirmed by the conclusion of the proposition in the last subsection. In order to be able to extend $f$ to vertices we have to require that $$\bigcap \{ f(x_1,...,x_m): x_i\in \operatorname{St}(V_i) \} \ne \emptyset,$$ for all vertices $V_1,...,V_m\in R_n$. Then we can assign $f(V_1,...,V_m)$ to be any vertex in this set.

Exercise. Prove that this set is a simplex.

Let's observe that with $f$ defined on the vertices we can use it to run elections with only pairwise votes. The outcome though is only a pairwise preference. Meanwhile, $f$ defined on the rest of the simplices gives us other elections with “partial” ballots.

The meaning of the above condition is that the pairwise preferences contained in the election rule are consistent but possibly ambiguous.

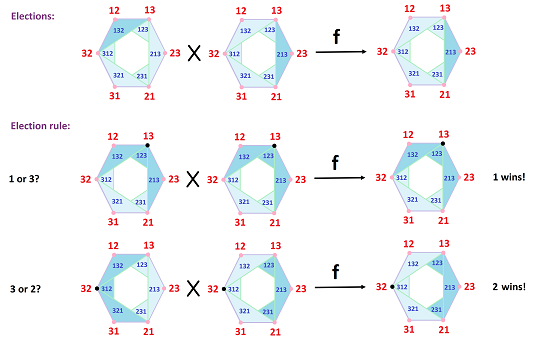
Independence of irrelevant alternatives. If two candidates are ranked relative to each other the same way by the same voters from the election to the next, then they are ranked this way by the election results as well:

• Given $a,b \in A$, $x=f(x_1,...,x_m),y=f(y_1,...,y_m)\in Z_n$, suppose $a<_{x_i} b$ if and only if $a<_{y_i} b$, then $a<_{x} b$ if and only if $a<_{y} b$.

Example. Below we illustrate this condition. We show one election, for $x$, and then what it tells us about the election rule, for two pairs of $a,b$:

Note that the complete votes that include a particular pairwise vote, such as $1>3$, correspond to the star of this vertex, such as $U_{13}$.

$\square$

Exercise. Sketch what happens to the rest of the stars under $f$.

Social choice: no fair elections

Next, we will apply the last theorem to the basic electoral system.

Suppose the number $n$ of alternatives/candidates is fixed: $$A:=\{1,2,...,n\}=\{C_1, C_2, ... ,C_n\}.$$ Voter $x$'s vote is a (strict) ordering of the alternatives: $$C_1 <_x C_2 <_x \ ... <_x C_n.$$ It is recorded as $$x=(C_1,C_2 , ... ,C_n).$$ The totality $Z$ of all possible votes/voters $R_n$ is the complex of orderings (or rankings) for the given $n$.

Suppose we have $m$ voters: $$V:=\{1,2,...,m\}.$$ Then an election is any combination of $m$ votes and the set of all possible elections is the product, $Z^m$. This is not a simplicial complex but a cell complex with cells given as products $$s=x_1 \times ... \times x_m$$ of some $N$-simplices $x_1, ..., x_m \in Z$. An election rule $$f: Z^m \to Z$$ converts any election, an element of $Z^m$, into a single vote, an element of $Z$: $$r=f(X)=f(x_1, ..., x_m).$$ Therefore outcome takes the same form, an ordering of the candidates: $$C_1 <_r C_2 <_r C_3 <_r \ ... <_r C_n.$$

Is $f$ a simplicial map? It is only a correspondence:

• $f$ takes each $Nm$-cell of $Z^m$ to an $N$-cell of $Z$.

Can we construct a simplicial map from $f$ by extending this correspondence to the rest of the cells of $Z^m$?

Therefore, to be able to extend $f$ to vertices we have to require that $$\bigcap \{ f(x_1,...,x_m): x_i\in \operatorname{St}(V_i) \} \ne \emptyset,$$ for all vertices $V_1,...,V_m\in Z$.

Then this is a social choice problem. The meaning of the axioms of social choice are clear:

Unanimity. If two candidates are ranked relative to each other the same way by all voters, then they are ranked this way by the election results as well:

• If $a<_x b$ for each $x\in V$, then $a<_r b$.

Anonymity. If two voters flip their preferences, it won't affect the results of the elections:

• Given $X=(x_1,...,x_m),\ Y=(y_1,...,y_m)\in Z^m$, suppose $x_i=y_i$ for all $i=1,...,m,\ i\ne p,q$ and $x_p=y_q,x_q=y_p$, then $f(X)=f(Y)$.

At this point the space of choices $Z$ has no topology! Recall however that $Z$ is the set of vertices of the complex of orderings $X=N_{\alpha}$:

This complex has non-trivial homology in one of the dimensions:

• $H_k(X)=0,\ k=1,2,...,n-3;$
• $H_{n-2}(X)={\bf Z}.$

Non-dictatorship. There is no voter whose preferences always win the elections:

• There is no $y \in V$ such that $a<_R b$ if and only if $a<_y b$.

Independence of irrelevant alternatives. If two candidates are ranked relative to each other the same way by the same voters from the election to the next, then they are ranked this way by the election results as well:

• Given $a,b \in A$, $X=(x_1,...,x_m),Y=(y_1,...,y_m)\in Z^m$, and $1\le p,q\le m$, suppose $a<_{x_i} b$ if and only if $a<_{y_i} b$, then $a<_{f(X)} b$ if and only if $a<_{f(Y)} b$.

Arrow’s Impossibility Theorem states that, when there are three or more candidates, no voting system can convert the preferences of all voters into a complete preference if it has to satisfy certain conditions.

Non-dictatorship. There is no voter whose preferences always win the elections:

• There is no $y \in V$ such that $a<_r b$ if and only if $a<_y b$.

The last condition is often criticized as too restrictive because it prohibits all “cyclic preferences”, such as:

• voter 1: $A < B < C$,
• voter 2: $B < C < A$,
• voter 3: $C < A < B$.

This is a fair criticism because, as we already know, this is exactly what prevents the space of choices from being acyclic which leads to the contradiction.

Then, alternatively, one ignores the last axiom and considers ballots as directed graphs on the set of $n$ vertices. Then the space of all ballots is acyclic. The outcome of the election can be chosen to be simply the sum of all pairwise votes. Under what circumstances this outcome can produce a decision function is addressed later.

A valid ballot is a complete acyclic directed graph on the set of $n$ vertices/candidates, while a ballot is a directed graph on the set of $n$ vertices. The space of all ballots is a simplex.

Social choice: utility functions

In this new light, we will consider again the issue of existence of utility functions.

Recall that when we consider $n+1$ possible events or outcomes, $A_0,...,A_n$, we place them at the vertices of an $n$-simplex $\sigma ^n=A_0...A_n$.

This probability simplex contains, in addition to these “primary” events, their convex combinations (lotteries).

A person's preferences are given by an order relation over the primary events, initially. And further these preferences may be captured by a utility function defined on the vertices of the simplex if it satisfies: $$x < y \Leftrightarrow u(x) < u(y).$$

And further these preferences may be captured by a utility function: $$u:\sigma ^n\to {\bf R},$$ that satisfies: $$x < y \Leftrightarrow E(u(x)) < E(u(y)),$$ where $E$ stands for the expected value.

A linear combination of the utilities of the primary outcomes: $$U(p_0,...,p_n)=\sum_i p_iu_i,$$ where $u_0,..., u_n$ are some numbers, is called the expected utility.

The expected utility exists under very natural restrictions, but only on the whole simplex! We state the following without proof.

Theorem (Von Neumann–Morgenstern Utility Theorem). Suppose two extra conditions are satisfied:

• continuity: if $x \le y \le z$, then there exists a probability $p\in [0,1]$ such that

$$px + (1-p)z = y;$$

• independence: if $x<y$ then for any $z$ and any $p\in (0,1]$,

$$px+(1-p)z < py+(1-p)y.$$ Then there is an expected utility.

Does an expected utility have to exist when some of the primary outcomes are incomparable?

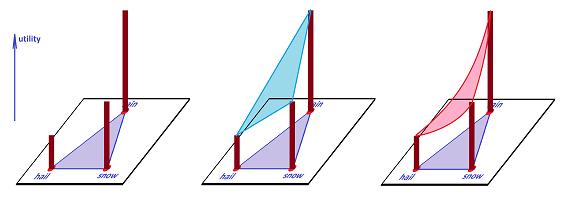
What do we mean by that? Does a utility exist for the simplicial complex with no edge between “death” and $\$ 10$? The simplicial complex of the camp sites on the lake shore contains no $2$-face so that even though the pairs $AB$, $BC$, and $AC$ are compatible and produce lotteries, the triple $ABC$ does not. So, is there a utility on this hollow triangle?

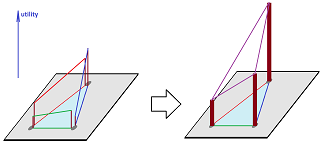
We assume that the preferences satisfy the conditions of the theorem on each simplex $a$ of the complex $K$, as a partial order: $x<_ay$. We also assume that these partial orders are compatible in the sense that two orders on two simplices coincide on their intersection, which is also a simplex: $$x<_ay \Leftrightarrow x<_by, \ \forall a,b\in K, x,y \in a\cap b.$$ Then there is an expected utility $u_a:a\to {\bf R}$ for each of the simplices $a\in K$. Can those be patched together? In other words, we want to construct a utility function $u:|K|\to {\bf R}$ for $K$ from those of the simplices: $$u\Big|_a=u_a, \ \forall a\in K.$$

We use the fact that adding a constant and multiplying by another will create a new expected utility for the set of preferences.

Corollary. Suppose the conditions of the theorem are satisfied for each simplex of the simplicial complex $K$. Suppose also that these orders are compatible. Suppose that the directed graph on $K^{(1)}$, the set of vertices and edges of $K$, created by the orders is acyclic. Then there is an expected utility for the whole $K$.

Proof. Every acyclic directed graph $G$ allows a topological sorting: $$(x,y)\in G \Leftrightarrow x<y.$$ The sorting is built as follows. (1) Start with a source $S$ and add it to top of the list. (2) Remove $s$ and all outgoing edges of $S$ from $G$. (3) Repeat. With the order of vertices found, apply the theorem to each $1$-simplex, $2$-simplex, etc. $\blacksquare$

Exercise. Provide the missing details of the proof.

Social choice: no fair elections

In a basic electoral system, we have $n$ candidates: $$A:=\{0,1,2,...,n-1\}=\{A_0,A_1, A_2, ... ,A_{n-1}\}.$$ and we suppose that these are the vertices of a simplicial complex $K$. We assume that the ring of coefficients $R$ is either ${\bf Z}$ or ${\bf R}$. A vote is an element of $C^∗(K)$. A election tally is a function $f: Q^m \to Q$ that converts an election, such as $Q=C^∗(K)$, into a single vote of the same type.

What makes an election fair?

The election tally $f:Q^m \to Q$ has to satisfy certain conditions.

Anonymity=Symmetry If two voters flip their votes, it won't affect the results of the elections: $$f(u)=f(s(u)),\ \forall u\in Q^m,\forall s\in \mathcal{S}_m.$$

Unanimity=Diagonality. If two candidates are compared to each other the same way by all voters, then they are compared this way by the election results as well: $$f(x,...,x)= x,\ \forall x\in Q.$$

Therefore, the tally $f$ is a mean.

We know that, over ${\bf R}$, there is only one such function, the mean tally: $$f(x_1,...,x_m)=\frac{1}{m}(x_1+...+x_m).$$

We also know that, over ${\bf Z}$, there is no such function.

Is there a tally if $Q=R$ is the set of the rankings of the candidates? We can convert the rankings to comparisons with a simple function $P:R\to C^1$ given by: $$0<_x 1 \Leftrightarrow x(01)=1.$$ We have demonstrated however that this scheme fails.

Arrow’s Impossibility Theorem states that, when there are three or more candidates, no voting system can convert the preferences of all voters into a complete preference if it has to satisfy certain conditions.

Unanimity. If two candidates are ranked relative to each other the same way by all voters, then they are ranked this way by the election results as well:

• If $a<_{x_i} b$ for each $x_i\in V$, then $a<_x b$, where $x=f(x_1,...,x_m)$.

Anonymity. If two voters flip their preferences, it won't affect the results of the elections:

• Given $u=(x_1,...,x_m),\ v=(y_1,...,y_m)\in R^m$, suppose $x_i=y_i$ for all $i=1,...,m,\ i\ne p,q$ and $x_p=y_q,x_q=y_p$, then $f(u)=f(v)$.

Independence of irrelevant alternatives. If two candidates are ranked relative to each other the same way by the same voters from the election to the next, then they are ranked this way by the election results as well:

• Given $a,b \in A$, $u=(x_1,...,x_m),v=(y_1,...,y_m)\in R^m$, and $1\le p,q\le m$, suppose $a<_{x_i} b$ if and only if $a<_{y_i} b$, then $a<_{f(u)} b$ if and only if $a<_{f(v)} b$.

Equilibrium of supply and demand

Recall that we have a “closed” market with $n+1$ commodities freely traded. The possible prices of these commodities form a price vector $p=(p_0,p_1,...,p_n)$.

We have shown that under the assumptions that

• the total bundle $\bar{c}$ is fixed;
• the money supply $W$ is fixed;

the space of prices is $$P:=\{p\in {\bf R}_+^{n+1}:\langle p,\bar{c} \rangle=W\},$$ which is a convex polyhedron.

Suppose there are also $m$ “agents” in the market, and each owns some combination of commodities:

• $c_j^i>0$ is how much $i$th agent owns of $j$th commodity.

Then

• $c^i=(c^i_1,...,c^i_{n+1})\in {\bf R}_+^{n+1}$ is $i$th agent's bundle of commodities.

Then,

• $w^i=\langle p, c^i\rangle$ is the $i$th agent's wealth.

These are the variables along with the prices.

By buying and selling these commodities the agent tries to maximize some utility $$u^i:{\bf R}^{n+1}_+\to {\bf R},$$ which is a function that depends on his ownership of commodities (but not the prices), subject to these (variable) wealth constraints: $$\langle p,x \rangle \le w^i.$$

A Walrasian equilibrium of the closed economy is a pricing $p\in P$ of all commodities along with a distribution $x^1,...,x^m\in {\bf R}_+^{n+1}$ of all commodities among the agents such that the following two conditions are satisfied:

• 1. the utilities are maximized:

$$x^i \in \arg\max \{u^i(x):\ x\in{\bf R}^{n+1}, \langle p,x \rangle \le w^i \},\ i=1,2,...,m,$$

• 2. the markets are cleared:

$$\sum_{i}x^i=\sum_i c^i =\bar{c}.$$

Note that this not an equilibrium of prices!

Theorem (Arrow-Debreu Equilibrium Theorem). Suppose the economy satisfies three assumptions about the utility functions $u^i=u^i(x_0,...,x_{n+1}),\ i=1,2,...,m$, with respect to each of its variables:

• (E1) $u^i$ is continuous;
• (E2) $u^i$ is increasing;
• (E3) $u^i$ is concave down.

Then there exists a Walrasian equilibrium $(p, x)$.

The $i$th agent wants a new bundle of commodities which depends on his wealth and the current prices:

• $d^i=d^i(p, w^i)$ is $i$th demand.

Then

• $z^i(p) = d^i(p, w^i) − c^i$ is $i$th excess demand.

Then

• $z(p) = \sum_{i}z^i(p)$ is the total excess demand.

The theorem follows from the Kakutani theorem.