Divergence

Suppose we have a flow on the plane and we want to compute how much of the liquid leaves (enters) a particular region $R$.

Suppose $F = ( p, q )$ is the velocity field for the flow. The idea is that we first break the region into small pieces and answer the question for each and then put the outcomes together. As the in-flow/out-flow of adjacent pieces cancel each other, the total of these numbers is the total amount of liquid leaving the region.

As we make each of these pieces smaller and smaller and it approaches a point, the out-flow will approach the divergence of $F$:

${\rm div \hspace{3pt}} F = \frac{\partial p}{\partial x} + \frac{\partial q}{\partial y}$ (pointwise).

As this process continues, the sums of out-flows will approach the integral of the divergence:

$$\int\int_R {\rm \hspace{3pt} div \hspace{3pt}} D dA.$$

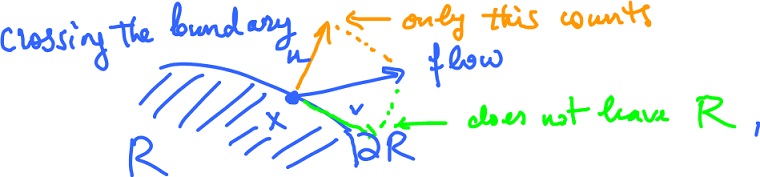
On the other hand, another way to solve the problem is simply watch how much liquid is crossing the boundary $\partial R$ of the region. In other words:

$$\int\int_R {\rm \hspace{3pt} div \hspace{3pt}} D dA = \displaystyle\int_{\partial R} ... ds.$$

Consider also the case of dimension $1$. Instead of a flow on the plane we have a flow in a piece of pipe, $R = [a,b]$. Once again we can look at the out-flow at each point and then add (integrate) the result or we can look at what is happening at the border, i.e., the end points:

$$\int\int_{[a,b]} F' dx = F(b) - F(a),$$

i.e., we have the Fundamental Theorem of Calculus. Thus, the divergence is simply a generalization of the derivative.

Back to dimension $2$. At the crossing of the boundary, note that the tangent (to $\partial R$) component of the velocity of the flow does not contribute to the amount of flow exiting/entering $R$:

Divergence Theorem. Let

$$F = ( f_1, f_2 ) $$

be a function with continuous derivative, and $R$ a simple region. Then

$$\int\int_R {\rm \hspace{3pt} div} F da = \int_{\partial R} F \cdot N ds,$$

where $N$ denotes a unit vector normal to $\partial R$ and $ds$ denotes the arc length.