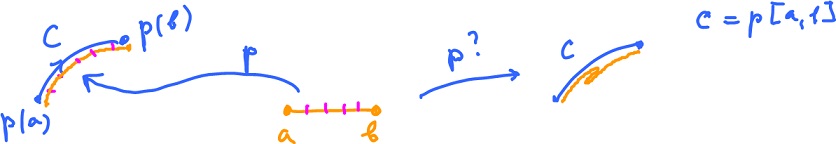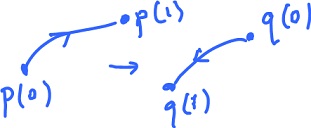This site is being phased out.
Discrete parametric curves
Contents
Dot product
Let's observe that we measure in ${\bf R}^1$, ${\bf R}^2$, ${\bf R}^3$, etc.
Consider the distance formula in ${\bf R}^2$.
Which is $$d=\sqrt{(a-u)^2+(b-v)^2},$$ that comes from Pythagorean Theorem.
In ${\bf R}^3$ also:
we have $$D=\sqrt{(a-u)^2+(b-v)^2+(c-w)^2}$$ etc.
Then, the distance from $d=(a,b)$ to $0$ is $\sqrt{a^2+b^2}$. $$D^2=d^2+c^2 = a^2+b^2+c^2,$$ diagonal of box $a \times b \times c$.
In ${\bf R}^n$ distance formula is the following.
The distance between $a=(a_1,\ldots,a_n)$ and $b=(b_1,\ldots,b_n)$ is $$d(a,b)=\sqrt{(a_1-b_1)^2+\ldots+(a_n-b_n)^2}.$$ (it's a number!)
Another measurement in the Euclidean space is angles.
Suppose we have $u,v \in {\bf R}^2$, so that $u=(u_1,u_2), v=(v_1,v_2)$.
Known formula: $$\cos \alpha=\frac{u_1v_1+u_2v_2}{\sqrt{u_1^2+u_2^2}\sqrt{v_1^2+v_2^2}}.$$ Here we identify the top to be the dot product of $u,v \in {\bf R}^2$ and the bottom is the norms of $u$ and $v$.
It is better notation then: $$= \frac{ < u,v > } {\lVert u \rVert \lVert v \rVert}.$$ Observation: no mention of dimension!
But does the angle between two vectors even make sense in ${\bf R}^n$?
Given $u,v \in {\bf R}^n$, what is the meaning of "the angle between vectors"?
First, we know what it is in ${\bf R}^2$.
Now, consider ${\bf R}^3$.
In ${\bf R}^3$, we make a plane $P={\rm span}\{u,v\}$ (the dimension is 2, a plane). Then we can measure the angle between these vectors -- within $P$!
Parametric curves
Simply put, curves are combinations of $n$ node functions $F: {\bf R} \to {\bf R}^q$ with $n=2,3,...$. The case of $n=1$ is familiar.
Example. Linear motion. Here
- $t$ is thought of as time,
- $f(t)$ is thought of as the position in space at time $t$.
$f(t) = v \cdot t$, a motion along a vector $v \in {\bf R}^n$ with constant speed $v$. Then the locations are $f(0) = 0, f(1) = 1$, etc.
Next, $$f(t) = v \cdot t + b$$ is also a line but the motion starts at $b \in {\bf R}^n$.
The backward linear motion is given by: $$g(t) = - v \cdot t = v \cdot (-t).$$ $\square$
In dimension $2$ we have two node functions: f_1, f_2, with the same domain, the $t$-axis, with the same nodes... Then, the $2$-dimensional node function (a curve) is $$f(t) = (f_1(t), f_2(t)).$$
Just as before we'll study
- derivative,
- integral.
Specifically, consider the following.
Example. Circular motion...
Centered at 0: $$f(t) = (\cos t, \sin t),$$ moving backward: $$f(t) = (\cos(-t), \sin(-t)),$$ with radius $r$: $$f(t) = r \cdot (\cos t, \sin t)$$ centered at point $(a,b)$: $$f(t) = (a,b) + r \cdot (\cos t, \sin t)$$ accelerated motion: $$f(t) = (\cos t^2, \sin t^2)$$ etc. $\square$
Example. Parabola: $$f(t) = (t, t^2).$$ The curve traces the parabola: $y = x^2$. $\square$
Example. Circle in $3$-space: $$f(t) = (\cos t, \sin t, 0),$$ located within the $xy$-plane. $\square$
Example. An ascending spiral (helix): $$f(t) = (\cos t, \sin t, t)$$ corresponding to $(x, y, z)$. $\square$
Tangents and derivatives
Recall some motivation for differential calculus, from Calc 1.
We want to study motion. Some questions we may ask are:
- On a winding road what is the direction of the headlights?
- Where does the rock go when released from the slingshot?
The answer is consider the tangents.
For the slingshot, we write $$f(x) = ( 1 - x^2 )^{\frac{1}{2}}$$ the graph of which is the circle. Then we differentiate and find the tangent line to the circle at any point: the slope] of the tangent line is equal to the value of the derivative of $f$ at the point.
There are some issues though. One is that strictly speaking the circle is given by $$f(x) = \pm ( 1 - x^2 )^{1/2},$$ with $\pm$. So, the method only works separately for the upper and lower halves of the circle. This is where parametric curves come handy.
Define $$g(t) := (\cos t, \sin t),\ t\in \left[ 0, \pi/4 \right].$$ Then the two node functions are $$x(t):=\sin t,\ y(t):=\sin t.$$
This is what we know: $$\begin{array}{lllll} (\sin t)'= \frac{\sin (h/2)}{h/2} \cos (t+h/2),\\ (\cos t)'=-\frac{\sin (h/2)}{h/2} \sin (t+h/2). \end{array}$$ These formulas give us the the $x$- and $y$-components of the velocity.
Then the velocity is: $$v(t) = g'(t)=(x',y').$$ then $$v(t)= \frac{\sin (h/2)}{h/2}\big( \cos (t+h/2), \sin (t+h/2) \big).$$
As we can see, the velocity vector also rotates.
What about the speed? $$s(t)=||v(t)||=\left| \frac{\sin (h/2)}{h/2} \right| \| \big( \cos (t+h/2), \sin (t+h/2) \big) \| = \left| \frac{\sin (h/2)}{h/2} \right| .$$ It is constant!
In the $n$-dimensional space, such a geometric approach is no longer appropriate. We have to rely on the algebra of vectors.
What is the rate of change of $f$? We have the same concepts:
- time change: $f(a + h) - f(a) - f(a)$ a vector, the displacement;
- location change: $h$ a number, the time passed.
Then the rate of change of $z$ with respect to $t$ can be expressed as $$f'(a) = \frac{f(a + h) - f(a)}{h}.$$ This is a vector.
The result is the same as before. Suppose $$f(t) = ( f_1(t), f_2(t) ),$$ then $$\begin{array}{} f'(a) &= \frac{\left( f_1(a + h), f_2(a + h) ) - ( f_1(a), f_2(a) \right)}{h} \\ &= \left( \frac{f_1(a + h) - f_1(a) )}{h}, \frac{f_2(a + h) - f_2(a)}{h} \right) \\ &= ( f'_1(a), f'_2(a) ). \end{array}$$
Theorem. The derivative $f'(a)$ is the vector of derivatives of the components of $f$: $$f'(a) = ( f'_1(a),f'_2(a) ).$$
Algebraic properties of the derivative
In this section we'll see how the derivative is affected by vector operations.
Addition and multiplication behave the exact same way as in dimension $1$, but there is no division...
Consider $f,g: {\bf R} \to {\bf R}^n$ and they have derivatives at a point $x = a$.
Sum rule. $$(f + g)' = f' + g'.$$
Proof. Coordinate-wise.
Scalar product rule. $$(\alpha f)' = \alpha \cdot f'.$$
Same proof as above.
Dot product rule. $$<f, g>' = <f', g> + <f, g'>.$$
Proof. $$\begin{array}{} &= (f_1 g_1, f_2 g_2, f_n g_n)', {\rm \hspace{3pt} where \hspace{3pt}} f_i, g_i: {\bf R} \to {\bf R} \\ &= (f'_1 g_1 + f_1 g'_1) + ... + (f'_n g_n + f_n g'_n) \\ &= (f'_1 g_1 + f'_2 g_2 + ... + f'_n g_n) + (f_1 g'_1 + f_2 g'_2 + ... + f_n g'_n) \\ &= <f', g> + <f, g'> \end{array}$$
Cross product rule. $$(f \times g)' = f' \times g + f \times g', (n = 3)$$
What about the norm $||f||$?
$$\begin{array}{} (||f||^2)' &= (<f, f>)' \\ &= <f', f> + <f, f'> \\ &= 2 <f', f>. \end{array}$$
Example. Consider rotation again. This means that we assume that $|| f ||$ constant, where $f$ is the location. Then $|| f ||^2$ = constant, differentiate the equation. $( (|| f ||)^2 )′ = 0$, so $2< f', f' > = 0$, thus $< f', f > = 0$. Hence
$$f' \perp f.$$
Example. What if the speed is constant? What is acceleration then? Let $g$ denote location, $g'$ velocity, $|| g' ||$ the speed. Using the previous example with $f = g'$, we obtain
$$f ⊥ f'$$
or, in our notation,
$$g' ⊥ g' '.$$
Chain Rule. Let $f: {\bf R} \to {\bf R}^n, g: {\bf R} \to {\bf R}$, then $fg: {\bf R} \to {\bf R}^n$ if domain $g \supset$ range $f$.
If $f'$ and $g'$ exist, then
$$(f \circ g)' = f' \circ g \cdot g'.$$
Lengths as integrals
Let $f$ be a parametric curve $$f : {\bf R} \to {\bf R}^n $$ and $b > a$. Define the length of the curve from $f(a)$ to $f(b)$.
The curve is made of segments: points $A_1, A_2, ..., A_s$ on the curve with $A_i = f( a_i), a_i < a_{i+1}$. The length of segment $[A_i, A_{i+1}]$ is $||A_i - A_{i+1}||.$ Then the total length is $$L({A_i}) \leq \displaystyle\sum_{i=1}^s||A_i - A_{i+1}||.$$
Find the angle of intersection of two curves: $$(\cos t, 3 \sin t) \quad (2 \cos t, \sin t).$$
We need to solve the equation: $$(\cos s, 3 \sin s) = (2 \cos t, \sin t)$$ with different parameters! This vector equation turns into two regular equations: $$\cos s = 2 \cos t,$$ and $$3 \sin s = \sin t,$$ from which we want to find $s$ and $t$. Then $$1 = \cos^2 t + \sin^2 t = (1 / 2 \cos s)^2 + (3 \sin s)^2.$$ Now solve for $s$, then find $t$. Compute the derivatives of these two functions for those values of $s$ and $t$. Find the angle by means of the dot product.
Example. The length of a circle of radius $r$ is equal to $2{\pi}r$. How do we know? Describe the circle as $$f(t) = r (\cos t, \sin t), t \in [0, 2{\pi}].$$ Now $$f'(t) = r ( -\sin t, \cos t)$$ and $$|| f'(t) || = r (\sin^2 t + \cos^2 t)^{\frac{1}{2}} = r.$$ Then $$L = \displaystyle\int_0^{2 \pi} r dt = rt |_0^{2 \pi} = r (2{\pi} - 0) = 2{\pi}r.$$
Re-parametrization
Example. Let $g$ parametrize a circle with $$g(t) = r(\cos (-t), \sin (-t)).$$ Then $|| g'(t) || = 1,$ i.e. by the formula the curve has the same length. Further, what about $$g(t) = r (\cos ({\pi} + t), \sin ({\pi} + t))?$$ Substituting for $\gamma = 3t$ yields $$g(t) = r (\cos 3t, \sin 3t), \ t \in [0, 2\pi / 3]$$ and $$|| g'(t) || = r \cdot 3.$$ Then $$L = \displaystyle\int_0^{\frac{2 {\pi}}{3}} 3r dt = \frac{6}{3} \pi r = 2\pi r.$$
A variety of parametrizations will produce the same result.
Is there a special one or the best one?
What if we follow the curve with the speed be equal to $1$? This is indeed special and there are only two ways to do that. So, if $|| f' || = 1$ for all $t$, this is called the natural parametrization of the curve.
Example. What is the natural parametrization of the circle? The "standard" parametrization $$g(t) = r (\cos t, \sin t)$$ is not natural because $|| g'(t) || = r.$ Consider $$f(t) = r (\cos\frac{t}{r}, \sin \frac{t}{r})$$ and $|| f'(t) || = r \cdot \frac{1}{r} = 1$. Observe that if $f$ is the natural parametrization, then $$L( f; [0, t] ) = t.$$
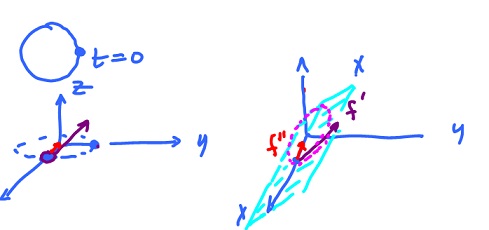
Example. Consider a helix $$f(t) = (\cos t, \sin t, t).$$ Then $$f'(t) = ( -\sin t, \cos t, 1)$$ and $$|| f'(t) || = ( (-\sin t)^2 + (\cos t)^2 + 1^2 )^{\frac{1}{2}} = \sqrt{2}.$$ Define $$g({\tau}) : \left( \cos \frac{\tau}{\sqrt{2}}, \sin \frac{\tau}{\sqrt{2}}, \frac{\tau}{\sqrt{2}} \right).$$ This is the natural parametrization and $\tau$ is called the natural parameter.
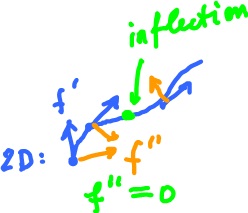
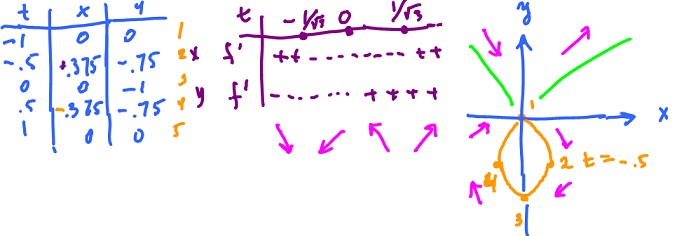
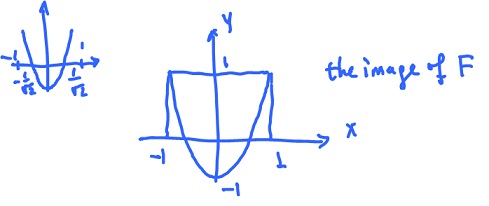
Review exercise. Plot the curve: $$F(t) = ( t (t^2 - 1), t^2 - 1 ).$$ Then $$F'(t) = ( 3t^2 - 1, 2t ).$$ Then $$F'(t)=0 iff t = \pm \frac{1}{\sqrt{3}}, 0.$$ Record the values of $F$ and $F'$ for a few values of $t$ in the table, then plot the curve:
Curvature
Let us first consider the circle again: $$g(t) = ( r \cos \tfrac{t}{r}, r \sin \tfrac{t}{r} )$$ with radius $r$. Then the tightness of the turn, the curvature, is the reciprocal of the radius: $$\kappa = \tfrac{1}{r}.$$
Definition. The curvature of the curve $z = g(t)$, where $t$ is the natural parameter, at $f(t)$ is defined by $$\kappa := || g' '(t) ||.$$
It's like the strength of the $g$-force that you have to deal with when turn...
Example. Circle: $$g'(t) = ( -\sin \tfrac{t}{r}, \cos \tfrac{t}{r} ),$$ $$g' '(t) = ( - \tfrac{1}{r} \cos \tfrac{t}{r}, - \tfrac{1}{r} \sin \tfrac{t}{r} ).$$ Therefore, $$\kappa = || g' '(t) || = \tfrac{1}{r} || ( \cos \tfrac{t}{r}, \sin \tfrac{t}{r} ) || = \tfrac{1}{r}.$$
Example. Helix: $$g(t) = ( \cos\tfrac{t}{\sqrt{2}}, \sin \tfrac{t}{\sqrt{2}}, \tfrac{t}{\sqrt{2}}),$$ (natural parameter). Then $$g'(t) = ( -\tfrac{1}{\sqrt{2}} \sin \tfrac{t}{\sqrt{2}}, \tfrac{1}{\sqrt{2}} \cos \tfrac{t}{\sqrt{2}}, \tfrac{1}{\sqrt{2}})$$ $$g' '(t) = ( -\tfrac{1}{2} \cos \tfrac{t}{\sqrt{2}}, -\tfrac{1}{2} \sin\tfrac{t}{\sqrt{2}}, 0)$$ and $$\kappa = || g' '(t) || = \tfrac{1}{2} || ( \cos \tfrac{t}{\sqrt{2}}, \sin \tfrac{t}{\sqrt{2}} ) || = \tfrac{1}{2}.$$
We define the radius of curvature as $\tfrac{1}{\kappa}$.
- Helix: $\tfrac{1}{\kappa} = 2$, radius $= 1$.
- Circle: $\tfrac{1}{\kappa} = 1$, radius $= 1$.
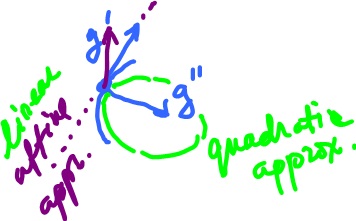
The osculating circle approximates the curve at the point and has radius equal to $\tfrac{1}{\kappa}$. This way the curvature of the circle is the same as that of the curve. The circle is located in the osculating plane determined by $g'$ and $g' '$, below.
Compare:
- $y = mx + b$ the best affine approximation, linear polynomial;
- $ax^2 + bx + c$, quadratic polynomial.
How do we find the osculating circle? Consider $f(t)$ at $t = a$, with $t$ the natural parameter. Compute $\kappa$, $R = \tfrac{1}{\chi}$.
The center of the circle is $$f(a) + R \tfrac{f' '(a)}{|| f' '(a) ||}= f(a) + \tfrac{1}{\kappa^2} f' '(a).$$
Example. Let us consider a helix, $a = 0, \kappa = 1 / 2, R = 2.$
Here
- $f(0) = ( 1, 0, 0 ),$
- $f'(0) = \left( 0, \tfrac{1}{\sqrt{2}}, \tfrac{1}{\sqrt{2}} \right),$
- $f' '(0) = ( -\tfrac{1}{2}, 0, 0).$
Example. Consider the curve $$G(s) = ( s \cos s, s \sin s, s^2 + 1 )$$ on the surface $$x^2 + y^2 = z - 1.$$ This is another way of representing the curve: $$x = s \cos s, y = s \sin s, z = s^2 + 1.$$ These $x, y, z$ have to satisfy the equation $$( s \cos s^2) + ( s \sin s)^2 = ( s^2 + 1 ) - 1$$ or $$s^2 {\rm cos}^2 s + s^2 {\rm sin}^2 s = s^2.$$
Now one can see from the Pythagorean Theorem that the equation $$s^2 ( \cos^2 s + \sin^2 s) = s^2$$ holds.
Review exercise. (1) Consider a ray from $( 0, 1, 0, 1)$ through $( 1, 0, 1, 0)$.
Write $f(t) = tu + P, t \geq 0$, where
- $u$: vector direction
- $P$: the initial point $f(0) = P$.
Let $P = ( 0, 1, 0, 1)$. What is $u$? Define point $Q$ as $Q = ( 1, 0, 1, 0)$, then $$\begin{array}{} u &= Q - P \\ &= ( 1, 0, 1, 0) - ( 0, 1, 0, 1) \\ &= ( 1, -1, 1, -1). \end{array}$$ Then the specific parametrization of the line is $$f(t) = t ( 1, -1, 1, -1) + ( 0, 1, 0, 1), t \geq 0.$$
(2) Consider $$F(t) = ( \cos t, \cos 2t), 0 \leq t \leq {\pi}.$$ What is the image of $F$? Let $x = \cos t$ and $y = \cos 2t = 2 \cos^2 t - 1 = 2x^2 - 1$ (parabola). Then $$x, y \in [ -1, 1].$$
Line integrals
Consider two main types of integrals we have seen.
Given motion with the position function $F : {\bf R} \to {\bf R}^n$ during a time interval $[ a, b ]$, we have two main "length characteristics":
- The displacement
$$= F(b) - F(a) = \displaystyle\int_a^b F'(t) dt = \displaystyle\int_a^b V(x) dx,$$ where $V$ is the velocity. (Also the work integral.)
- The distance traveled
$$= \displaystyle\int_a^b || F'(t) || dt,$$ where curve $C$ is the image of $F$, so this is the arc length of a parametric curve. (Also the surface area integral.)
The usual, displacement integral satisfies these properties.
Linearity: $$\displaystyle\int_G ( f(x) + g(x) ) dx = \displaystyle\int_G f(x) dx + \displaystyle\int_G g(x) dx {\rm \hspace{3pt} (Sum \hspace{3pt} Rule)};$$ $$\displaystyle\int_G k f(x) dx = k \displaystyle\int_G f(x) dx {\rm \hspace{3pt} (Constant \hspace{3pt} Multiple \hspace{3pt} Rule).}$$
Additivity: $$\displaystyle\int_{A \cup B} f(x) dx = \displaystyle\int_A f(x) dx + \displaystyle\int_B f(x) dx, {\rm \hspace{3pt} with \hspace{3pt}} (A \cap B) = 0,$$ in particular, $$\displaystyle\int_{[a,b] \cup [c,d]} f(x) dx = \displaystyle\int_{[a,b]} f(x) dx + \displaystyle\int_{[c,d]} f(x) dx$$
But these properties don't fully apply to the arc length integral. What is the difference?
Observe how differently the two integrals behave when the motion changes direction, from $b$ to $a$:
$$\displaystyle\int_a^b V(x) dx = - \displaystyle\int_B^a V(x) dx,$$ but $$\displaystyle\int_a^b || F'(t) || dt = \displaystyle\int_B^a || F'(t) || dt.$$
Orientation: $$\displaystyle\int_{-A} f(x) dx = - \displaystyle\int_A f(x) dx,$$ which is easy to understand if these are intervals: $$\displaystyle\int_{-[a,b]} f(x) dx = - \displaystyle\int_{[a,b]} f(x) dx = \displaystyle\int_{[b,a]} f(x) dx.$$
The difference comes from either treating the intervals as
- sets: $[ a, b ] = [ b, a ]$;
or as
- oriented sets: $[ a, b ] = -[ b, a ]$.
The orientation of a curve
It comes from its parametrization. For the curves in figure there are two possible orientations (and infinite many parametrizations). For example, given parametrization $p(s)$, $$q(s) = p(1 - s)$$ is another parametrization that produces the opposite orientation to the one from $p$.
Given a parametrization $$p: [ a, b ] \to {\bf R}^n, $$ then $C = p( [ a, b ] )$ is a curve.
Question: What happens to the displacement when the motion changes direction?
Answer: It changes its sign.
In terms of integrals: $$\int_a^b V(x) dx = - \int_b^a V(x) dx,$$ where $V$ is the velocity.
This is where it comes from: $$\int_{-[a,b]} f(x) dx = - \int_{[a,b]} f(x) dx = \int_{[b,a]} f(x) dx.$$
Note: There is a difference when you treat the domain of integration as
- an interval: $[ a, b ] = [ b, a ]$;
or as
- an oriented interval: $[ a, b ] = -[ b, a ]$.
More generally, $$\int_{-A} f(x) dx = - \int_A f(x) dx.$$
This may be the flow integral, for example.
Consider a curve given by $p:[0,1] \rightarrow R$. Then $q:[0,1] \rightarrow R$ given by $$q(s) = p(1 - s)$$ is another parametrization that produces the opposite orientation to the one from $p$.
For the curves in the picture there are two possible orientations (and infinite many parametrizations).
A parametrization that isn't one-to-one (on the right) is not good for computing the arc length, but fine for line integrals: displacement, work, etc.
Work
Suppose we want to compute the work $W$ of a constant force $F$ along a straight path. As we know in this case $$W = force \cdot distance.$$ This simple formula though only works if we take into account the direction of motion. Consider the special case when you move forward and then back. Then the work breaks into two parts and they cancel each other. To clarify the situation, we parametrize the motion as: $$p: [ 0, 2 ] \to C = [ 0, 1 ], $$ Then $$\begin{array}{} p(t) &= t & \text{ if } t \in [0,1],\ p'(t)=1, \\ &=(2-t) & \text{ if } t \in [1,2],\ p'(t)=-1 ; \\ p(0) &= p(2) = 0 \end{array}$$ Then,
the velocity $= 1$ during [ 0, 1 ]; $= -1$ during $[ 1, 2 ]$.
Then
The idea is that we should amend the formula as:
where unit velocity is the unit vector in the direction of the motion:
Moreover,
with summation over periods of constant velocity and force.
The need for this term becomes clearer in the case $\dim = 2$.
Suppose $V$ is the velocity vector. Observe that $$W = 0 \text{ if } F \perp V.$$ More generally, $F^*$ matters when calculating the work, $F^*$ being the projection of $F$ on $V$. Thus,
where $s$ is the distance. Note that in this formula $F$ is a vector field.
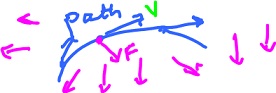
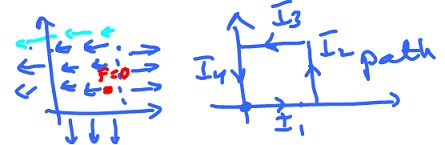
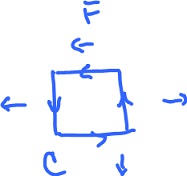
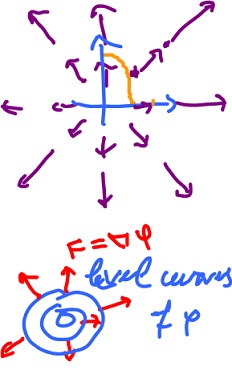
Example. Find the work $$W = \displaystyle\sum_i F_i \cdot V_i \cdot \Delta s_i$$ while moving through the force field $F$ displayed along the square path counterclockwise. Observe $$||F|| = 1, ||V|| = 1.$$ Compute work along each of the straight segments: $$\begin{array}{lll} I_1: W = ( 0, -1 ) ( 1, 0 ) = 0;\\ I_2: W = ( 1, 0 ) ( 0, 1 ) = 0;\\ I_3: W = ( -1, 0 ) ( -1, 0 ) = 1;\\ I_4: W = ( -1, 0 ) ( 0, -1 ) = 0. \end{array}$$ Then $$W = 0 + 0 + 1 + 0 = 1.$$
To summarize, if the force $F$ is constant and the velocity $V$ is constant then the work is found by $$W = F \cdot V \Delta s,$$ where the $\cdot$ is the dot product, $V$ is the unit vector of the velocity and $\Delta s$ is the distance.
Now what if we have a parametric curve $C$? Then we represent the curve (and the motion) by a sequence of segments so that with constant $F$ and $V$ in each: $$F = F_i \text{ on } C_i,$$ $$V = V_i \text{ on } C_i.$$ Then $$W_i = F_i \cdot V_i l(C_i),$$ where $l(C_i)$ is the length of $C_i$. The total work is then $$W = \displaystyle\sum_{i=1}^n F_i \cdot V_i l(C_i).$$
We assume that
- the force field is a piece-wise constant field;
- the curve is a parametric curve.
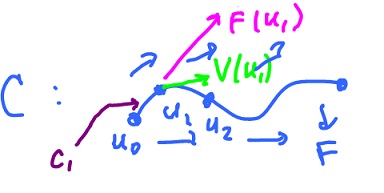
Then $C_i$ which goes from $u_{i-1}$ to $u_i$. Now we define the work as $$W = \displaystyle\sum_{i=1}^n F(u_i) \cdot V(u_i) l(C_i).$$
If we assume that such a limit exists (it does when $F$ is continuous and the curve is continuously differentiable), then we define the line integral $$\displaystyle\int_C F \cdot V ds $$ as this limit.
Example. Let $$F( x, y ) = ( x + y, x^2 y ),$$ $$V ds = ( dx, dy ).$$ Then $$F \cdot V ds = ( x + y, x^2 y ) \cdot ( dx, dy ) = ( x + y ) dx + x^2 y dy.$$ So the work is equal to $$W = \displaystyle\int_C ( x + y ) dx + x^2 y dy.$$
Now we need a parametrization, and we choose to parametrize $C$ as: $$p: [ a, b ] \to {\bf R}^2;$$ $$u_i = p(t_i).$$
$$\begin{array}{} \displaystyle\int_C ... &= \displaystyle\sum_{i=1}^n F(u_i) \cdot V(u_i) l(C_i) \\ &\approx \displaystyle\sum_{i=1}^n F(u_i) \cdot \frac{p'(t_i)}{||p'(t_i)||} ||p'(t_i)|| h, \end{array}$$ where we have expressed the velocity unit vector as $\frac{p'(t_i)}{||p'(t_i)||}$, and the the distance covered in the time interval ${\Delta}t$ as the product $||p'(t_i)|| h$ (speed $\cdot$ time). And thus we have $$\displaystyle\int_C ... = \displaystyle\sum_{i=1}^n F(u_i) \cdot p'(t_i) h,$$ which is the integral $$\displaystyle\int_a^b F( p(t) ) \cdot p'(t) dt.$$
Example. Compute the line integral $$\displaystyle\int_C 2x dx + 6( x - y ) dy$$ with $$C: p(t) = ( t, t ), 0 \leq t \leq 1.$$ Here the force is $F = ( 2x, 6( x - y) )$, while $dW = ( dx, dy )$. Moreover, $a = 0$ and $b = 1$. Since $$p'(t) = ( 1, 1 ),$$ the integral turns out to be $$\begin{array}{} \displaystyle\int_C F \cdot dW &= \displaystyle\int_a^b ( 2t, 6( t - t ) ) \cdot ( 1, 1 ) dt \\ &= \displaystyle\int_0^1 ( 2t, 0 ) \cdot ( 1, 1 ) dt \\ &= \displaystyle\int_0^1 2t dt \\ &= t^2 \Big|_0^1 \\ &= 1. \end{array}$$ $\square$
Examples of line integrals
Example. Compute
$$\displaystyle\int_C ( x_2, x_3, x_1 ) \cdot dX, {\rm \hspace{3pt} where}$$
$$C: p(t) = ( {\rm cos}(t), {\rm sin}(t), t ) = ( X_1, X_2, X_3 ), 0 \leq t \leq 2{\pi}.$$
In this case we have
$$F( x_1, x_2, x_3 ) = ( x_2, x_3, x_1 )$$
and
$$p'(t) = ( -{\rm sin}(t), {\rm cos}(t), 1 ).$$
Putting everything together one obtains
$$\begin{array}{} \displaystyle\int_C ... &= \displaystyle\int_a^b F( p(t) ) \cdot p'(t) dt \\ &= \displaystyle\int_0^{2 \pi} ( {\rm sin}(t), t, {\rm cos}(t) ) \cdot ( -{\rm sin}(t), {\rm cos}(t), 1 ) dt \\ &= \displaystyle\int_0^{2 \pi} ( -{\rm sin}^2(t) + t{\rm \hspace{3pt} cos}(t) + {\rm \hspace{3pt} cos}(t) ) dt. \end{array}$$
Here then one integrates, the first term through a change of variables $u = {\rm \hspace{3pt} cos}(t)$, the second term by parts, and the last term directly.
Example. Compute $\displaystyle\int ( 2x dx + 6( x - y ) dy )$ with
Now parametrize $C$:
$$p(t) = ( t, -t ), {\rm \hspace{3pt} with \hspace{3pt}} -1 \leq t \leq 2.$$
Then
$$p'(t) = ( 1, -1 ).$$
Finally, $$\begin{array}{} \displaystyle\int ... &= \displaystyle\int_{-1}^2 ( 2t, 6( t + t ) ) \cdot ( 1, -1 ) dt \\ &= \displaystyle\int_{-1}^2 ( -10t ) dt = -5t^2 |_{-1}^2 \\ &= -20 + 5 \\ &= -15. \end{array}$$
Properties of line integrals
Additivity: $$\displaystyle\int_{C_1 \cup C_2} F \cdot dX = \displaystyle\int_{C_1} F \cdot dX + \displaystyle\int_{C_2} F \cdot dX.$$
Here the parametrizations should match $$C_1 \cup C_2: [ a, c ] \to C_1: [ a, b ] \& C_2: [ b, c ].$$
Linearity: $$\displaystyle\int_C ( F + G ) \cdot dX = \displaystyle\int_C F \cdot dX + \displaystyle\int_C G \cdot dX;$$ $$\displaystyle\int_C ( k F ) \cdot dX = k \displaystyle\int_C F \cdot dX.$$ (follow from the formula) We now know that $$\displaystyle\int_C F \cdot dX = \displaystyle\int_a^b F( p(t) ) \cdot p'(t) dt;$$ what can we say if $||F|| \leq M$? We consider $$\begin{array}{} | \displaystyle\int_C F \cdot dX | &= | \displaystyle\int_a^b F( p(t) ) \cdot p'(t) dt | \\ &\leq \displaystyle\int_a^b | F( p(t) ) \cdot p'(t) | dt \\ &\leq \displaystyle\int_a^b || F( p(t) ) || || p'(t) || dt \\ &\leq \displaystyle\int_a^b M || p'(t) || dt \\ &= M \displaystyle\int_a^b || p'(t) || dt , \end{array}$$ and we recognize $(\displaystyle\int_a^b || p'(t) || dt )$ as the arc length of $C$. It follows then:
Theorem. If $||F|| \leq M$ on $C$ , then $$\left| \displaystyle\int_C F \cdot dX \right| \leq M \cdot ({\rm \hspace{3pt} length \hspace{3pt} of \hspace{3pt}} C).$$
If we reverse orientation of the curve, we get $$C: X = p(t), t {\in} [ a, b ];$$ $$-C: q(t) = p( b + a - t ), t {\in} [ a, b ];$$ $$q'(t) = -p'( b + a - t).$$ It follows then:
Theorem. If $-C$ is $C$ with reversed orientation, then $$\displaystyle\int_{-C} F \cdot dX = - \displaystyle\int_C F \cdot dX.$$
Orthogonality. If $C$ is vertical (horizontal) in ${\bf R}^2$, and $F = ( f_1, 0 ) ( F = ( 0, f_2)$, respectively ), then $$\displaystyle\int_C F \cdot dX = 0.$$
Proof. Easy: $$C: p(t) = ( 0, r(t) ), t {\in} [ a, b ];$$ Then, $$\begin{array}{} \displaystyle\int_C ( f_1, 0 ) \cdot dX &= \displaystyle\int_a^b ( f_1(t), 0 ) \cdot ( 0, r'(t) ) dt \\ &= \displaystyle\int_a^b ( f_1(t) \cdot 0 + 0 \cdot r'(t) ) dt = 0. QED \end{array}$$ $\blacksquare$
It follows then the integral along the circle that lies in the $x_2x_2$-plane for the force along the $x_a$ axis is $0$: $$\displaystyle\int_a^b ( f_1, 0, 0, ) \cdot ( 0, r'(t), s'(t) ) dt = 0.$$ with $$r(t) = \cos (t);$$ $$s(t) = \sin(t)}.$$ The integral after parametrization becomes $$\displaystyle\int_0^{2 \pi} ( f r'(t) - f s'(t) ) dt = ?$$ (here the integrand is different from zero).
Independence of path
When does the work integral along curve $C$ $$\displaystyle\int_C F dV$$ depend only on the initial and final points of $C$?
Example. Suppose $C$ is a closed curve on the plane. Since the initial point is equal to the final point of $C$, if the integral is path independent, we have $$\displaystyle\int_C F dV = 0.$$ Now, by the Jordan Theorem, it follows that $C$ bounds a region $R$. Then by the Stokes Theorem, $$0 = \displaystyle\int_{C= \partial R} F dV = \displaystyle\int\displaystyle\int_R 1 dA.$$ This certainly wouldn't work for all possible $F$. For example, if $$F = ( 0, x ),$$ then $$\displaystyle\int\displaystyle\int_R 1 dA =\text{ area of }R \neq 0.$$
Example. Suppose $F$ is the force field of gravity: $$F = ( 0, g_m ),$$ where $g_m$ is the gravitational constant. Let us determine if it is path independent: $$\displaystyle\int_C F dV = \displaystyle\int_a^b ( 0, g_m ) p'(t) dt$$ with the parametrization $p(t), t \in [ a, b ]$. The above is equal to $$\begin{array}{} \displaystyle\int_a^b g_m p'_2(t) dt &= g_m \displaystyle\int_a^b p'_2(t) dt \\ &= g_m ( p_2(b) - p_2(a) ) \end{array}$$ with the Fundamental Theorem of Calculus. Now $$g_m ( p_2(b) - p_2(a) ) = g_m ( B_2 - A_2 ),$$ where $A$ and $B$ are the end points of $C$. So, the answer is Yes.
The same holds for any other constant force $F$.
If the work is independent of path, the force is called conservative.
It is sufficient for the force to have a potential function: $$F =\nabla \varphi.$$
Theorem. If $F$ has a potential function, then it is conservative:
i.e. $$\displaystyle\int_{C_1} F dV = \displaystyle\int_{C_2} F dV$$ for all curves $C_1, C_2$ with the same end points.
Proof. Simply compute the line integral for a specific parametrization $p$ of $C$: $$\begin{array}{} \displaystyle\int_C F dV &= \displaystyle\int_a^b F( p(t) ) p'(t) dt \\ &= \displaystyle\int_a^b ∇ {\varphi}( p(t) ) p'(t) dt {\rm \hspace{3pt} (right-hand \hspace{3pt} side \hspace{3pt} of \hspace{3pt} chain \hspace{3pt} rule)} \\ &= \displaystyle\int_a^b d / dt {\varphi}( p(t) ) dt \\ &= {\varphi}( p(b) ) - {\varphi}( p(a) ) {\rm \hspace{3pt} (Fundamental \hspace{3pt} Theorem \hspace{3pt} of \hspace{3pt} Calculus)} \\ &= {\varphi}( A ) - {\varphi}( B ), \end{array}$$ where $A$ and $B$ are the end points of $C$. QED
Corollary. If $$F = \nabla {\varphi}$$ under the conditions of the above theorem, then $$\displaystyle\int_C F dV = {\varphi}( B ) - {\varphi}( A ).$$
Example. Let $F( x, y ) = ( x, y )$, and $C$ the image of $( \cos t, 2 \sin t )$ for $t \in [ 0, \frac{\pi}{2} ]$. Then find ${\varphi}$ satisfying: $$\nabla {\varphi} = ( x, y ).$$ Then $$\frac{{\partial}{\varphi}}{\partial x} = x, \frac{d{\varphi}}{dy} = y.$$ Hence $${\varphi}( x, y ) = \displaystyle\int x dx = \frac{x^2}{2} + C(y),$$ $${\varphi}( x, y ) = \displaystyle\int y dy = \frac{y^2}{2} + D(x),$$ thus together we obtain $${\varphi}( x, y ) = \frac{x^2}{2} + \frac{y^2}{2}.$$
Now $$\begin{array}{} \displaystyle\int_C F dV &= {\varphi}( {\rm end \hspace{3pt} point} ) - {\varphi}( {\rm initial \hspace{3pt} point} ) \\ &= {\varphi}( {\rm cos \hspace{3pt}} \frac{\pi}{2}, 2 {\rm sin \hspace{3pt}} \frac{\pi}{2} ) - {\varphi}( {\rm cos \hspace{3pt}} 0, 2 {\rm sin \hspace{3pt}} 0 ) \\ &= {\varphi}( 0, 2 ) - {\varphi}( 1, 0 ) \\ &= \frac{2^2}{2} - \frac{1^2}{2} \\ &= \frac{3}{2}. \end{array}$$
Example. Let $F( x, y ) = ( e^y, x e^y )$. Then $$\frac{{\partial}{\varphi}}{\partial x} = e^y, \frac{d{\varphi}}{dy} = x e^y,$$ hence $$\varphi( x, y ) = x e^y + C(y),$$ $$\varphi( x, y ) = x e^y + D(x).$$ Combining, we obtain $$\varphi( x, y ) = x e^y.$$
Example. Let $F = ( 0, x ).$ To find ${\varphi}$, solve $$\frac{{\partial}{\varphi}}{\partial x} = 0, \frac{d{\varphi}}{dy} = x,$$ then $$\varphi = C(y) = xy + D(x).$$ Here the left-hand side depends only on $x$ and the right-hand side depends only on $y$. This is impossible. So, this force does no have a potential function.
Theorem. Suppose $F = ( F_1, ..., F_n )$ has continuous partial derivatives on an open ball $R$. If $$\frac{{\partial}F_i}{{\partial}x_j} = \frac{{\partial}F_j}{{\partial}x_i},$$ then $F$ is conservative.
Example. Consider $F = ( F_1, F_2 ) = ( 0, x )$, then $$\frac{{\partial}F_1}{{\partial}x_2} = 0 \neq \frac{{\partial}F_2}{{\partial}x_1} = 1.$$
Theorem. Assume $R$ is path connected. Then the following are equivalent:
- $\displaystyle\int_C F dV$ is path independent,
- $F = \nabla \varphi$,
- $\displaystyle\int_C F dV = 0$, and $C$ is a closed curve.
Proof. $(1) \Rightarrow (2)$. Define $$\varphi(x) = \displaystyle\int_C F dV,$$ where $C$ is a curve from a fixed point $x_0$ to $x$. Note that $F$ is integrable on any $[ a, x ] \subset [ a, b ]$. Then define $$F(x) = \displaystyle\int_a^x f(x) dx.$$ $\blacksquare$