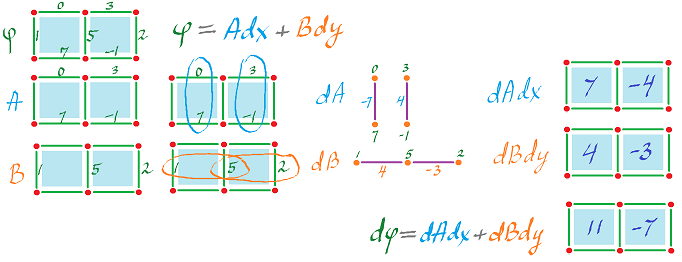This site is being phased out.
Calculus of discrete differential forms
Redirect to:
Introduction
The difference between "calculus" and "exterior calculus" will become clearer in the discrete environment. Indeed, in the continuous environment, we have the counterparts:
The difference might appear -- based on our calc 1 experience -- minor or even artificial (same thing with some weird tail attached).
In the discrete set-up the choice to be made is clearer as now we deal with
The latter is simply the difference (cf. difference equations and finite differences).
The functions are discrete and defined, for example, on $...-1,0,2,3,4,...$. They change abruptly and, of course, the change is simply the difference of values: $$f(n+1)-f(n).$$ The only question is where to put this value? What is the domain of this new function?
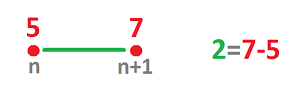
The picture below suggests where:
It should be assigned to the edge that connects $n$ to $n+1$. Where else would it go?
Let's take a look at this from the point of view of our study of motion with, say, function $p$ giving the position. Suppose
- at time $n$ hours we are at the $5$ mile mark: $p(n)=5$, and then
- at time $n+1$ hours we are at the $7$ mile mark: $p(n+1)=7$.
We don't know what exactly has happened during this hour. However, the simplest assumption would be that we have been waking at a constant speed of $2$ miles per hour. Now, instead of our velocity function $v$ assigning this value to each instant of time during this period, it is assigned to the whole interval: $$v\Bigg( [n,n+1] \Bigg)=2,$$ or sometimes simply: $$v [n,n+1]=2.$$ This way the elements of the domain of the velocity function are the edges.
The relation between a discrete function and its derivative is illustrated below:
This idea makes sense from the point of view of differential forms -- both continuous and discrete -- that we have studied. Indeed,
- $f$ is a $0$-form, i.e., a function defined on the $0$-cells (a cochain), and
- its derivative $df$ should be a $1$-form, defined on $1$-cells.
In other words: $$df[n,n+1]=f(n+1)-f(n).$$ This will be our definition.
Of course, if the interval was of length $h$ we would see the obvious difference between derivative and exterior derivative as the former would be $\frac{f(n+h)-f(n)}{h}$ while the latter would remain essentially unchanged as $f(n+h)-f(n)$.
Exterior derivative of $0$-forms
We continue with cubical $0$-forms. What is the exterior derivative $$d:C^0({\bf R})\rightarrow C^1({\bf R})? $$
Let's approach this from the point of view of the Fundamental Theorem of Calculus. Given $f \in C^0({\bf R})$, we use our definition of $df \in C^1({\bf R})$ as $$df([a,a+1]) = (f(a+1) - f(a))$$ to re-write the FTC: $$\displaystyle\int_{[a,a+1]} df = f(a+1) - f(a).$$ Observe that here $[a,a+1]$ is a $1$-cell and $\{a+1\},\{a\}$ make up the boundary of this cell. In fact, $$\partial [a,a+1]=\{a+1\}-\{a\}$$ taking into account the orientation.
Note: $[a,a+1]$ can be replaced with $[a,a+h]$ for a grid of size $h$. But, for now, there is no geometry...
What about integration over "longer" intervals?
Easy: for $a,k \in {\bf Z}$, $$\begin{align*} \displaystyle\int_{[a,a+k]} df \\ &= \displaystyle\int_{[a,a+1]} df + \displaystyle\int_{[a+1,a+2]}df + \ldots + \displaystyle\int_{[a+k-1,a+k]} df \\ &= f(a+1)-f(a) + f(a+2) - f(a+1) + \ldots + f(a+k) - f(a+(k-1)) \\ &= f(a+k) -f(a). \end{align*}$$ We just applied the definition repeatedly.
Thus, the FTS still holds, in its net change form.
In fact, we can now rewrite this in a fully algebraic form. Indeed, $$\sigma = [a,a+1]+[a+1,a+2]+...+[a+k-1,a+k]$$ is a $1$-chain and $df$ is a $1$-cochain. Then the above computation takes this form $$\begin{align*} df(\sigma) \\ &= df([a,a+1]+[a+1,a+2]+...+[a+k-1,a+k]) \\ &= df([a,a+1])+df([a+1,a+2])+...+df([a+k-1,a+k]) \\ &= f(a+k) -f(a) \\ &= f(\partial[a,a+k]). \end{align*}$$
The resulting interaction of the operators of exterior derivative and boundary $$df(\sigma) =f(\partial\sigma)$$ is an instance of the General Stokes Theorem.
Our definition, and the theorem, is applicable to any cubical complex $R \subset {\bf R}$ because, by definition, it is a set of cells such that if cell $s \in R$, then all of its boundary cells also belong to $R$. So, all the end-points are included and $df$ can always be computed.
Let's consider simple cases.
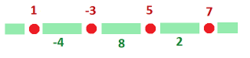
Dimension $1$ -- degree $1$. Given a $0$-form $f$ (in red) we compute its exterior derivative $df$ (in green):
Observe that the old formula for continuous forms, $$df = f' dx,$$ still works. Except now the derivative, if ever there is a need for it, is understood as defined on intervals: $$f' = f(a+1)-f(a).$$
So to summarize,
Dimension $2$ -- degree $1$. Given a $0$-form $f$ (in red) we compute its exterior derivative $df$ (in green):
Once again, it is computed by taking differences.
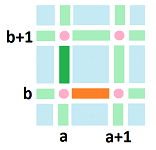
Let's make this more specific. We consider the differences horizontally (orange) and vertically (green):
and, thus, we have our definition:
- (orange) $df([a,a+1] \times \{b\}) = f\Bigg(\{(a+1,b)\}\Bigg) - f\Bigg(\{(a,b)\}\Bigg)$
and
- (green) $df(\{a \} \times [b,b+1]) = f\Bigg(\{(a, b+1)\}\Bigg) - f\Bigg(\{(a,b)\}\Bigg)$.
Once again we have a discrete analogue of a formula for continuous forms: $$df = \nabla f \cdot dA,$$ where $dA = (dx,dy)$ and $\nabla f = (f'_x,f'_y)$. The formula is justified if we interpret the above as:
- $f'_x([a,a+1] \times \{b\}) = f(a+1,b) - f(a,b)$
- $f'_y(\{a \} \times [b,b+1]) = f(a, b+1) - f(a,b)$.
Exterior derivative of $1$-forms
What about the higher degree exterior derivatives?
Recall that we have used the computational definition (below) to discover, inductively, the exterior derivative for continuous forms, so let's try to apply it to discrete (cubical) forms in the same fashion. The definition will look like this:
Definition: If $\varphi \in C^k$ then $d \varphi \in C^{k+1}$ and $d \varphi$ is obtained from $\varphi$ by applying $d$ to each of the coefficient functions involved in $\varphi$.
Let's start with dimension $2$. We've seen this before, if $$\varphi = A dx + B dy,$$ then $$d \varphi = dA \wedge dx + dB \wedge dy,$$ with $\wedge$ sometimes omitted.
Let's apply this definition to the cochain representation.
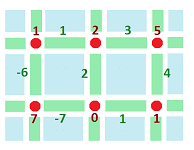
We need to find the value of the $2$-form $d \varphi$ on the $2$-cells $\alpha$ and $\beta$. We subtract vertically and horizontally, as before, and then add:
Here are the details:
- $dA = (0-7)dy = -7 dy,$ on $\alpha$,
or rather its $1$-dimensional substitute as shown in the third column. Also
- $dA = (3 - (-1))dy = 4 dy$ on $\beta$.
Further,
- $dB = (5-1)dx = 4dx$ on $\alpha$,
- $dB = (2-5)dx = -3dx$ on $\beta$.
So, on $\alpha$, using antisymmetry to get the third line, $$\begin{align*} d \varphi &= dA \wedge dx + dB \wedge dy\\ &= -7 dy \wedge dx + 4 dx \wedge dy \\ &= 7 dx \wedge dy + 4 dx \wedge dy \\ &= 11 dx \wedge dy. \end{align*}$$ Similarly, on $\beta$: $$d \varphi = -7 dx \wedge dy.$$ Here, we have used $(5-1) - (0-7)=11$ and $(2-5) - (3-(-1)) = -7$ respectively to compute the coefficients. Thus, what we end up with is:
Which is very similar to the formula for continuous forms: $$d(A dx + B dy) = (B_x - A_y)dx \hspace{1pt} dy.$$
This isn't all though...
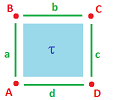
Suppose a $1$-form $\varphi$ is defined on this single cell cubical complex:
Then, by definition, $$d \varphi(\tau) = \Bigg(\varphi(c) - \varphi(a) \Bigg) + \Bigg( \varphi(b) - \varphi(d) \Bigg).$$ What is the point? Let's rearrange the terms: $$d \varphi(\tau) = \varphi(d) + \varphi(c) - \varphi(b) - \varphi(a).$$ In other words we go full circle around $\tau$, counterclockwise with the correct orientation!
Of course we recognize this as a line integral. We can read this as follows: $$\int_{\tau}d \varphi=\int _{\partial \tau} \varphi.$$ Algebraically: $$d \varphi(\tau) = \varphi(d) + \varphi(c) + \varphi(-b) + \varphi(-a)= \varphi(d+c-b -a) = \varphi(\partial\tau). $$
The resulting interaction of the operators of exterior derivative and boundary is the same as for dimension $1$ discussed above: $$d\varphi =\varphi\partial,$$ and, again, it is an instance of the General Stokes Theorem.