This site is being phased out.
Differential Equations -- Spring 2017
MTH 335 - Differential Equations. First and second-order ordinary differential equations. Applications include vibrations and electrical circuits. Laplace transform, approximate solutions, orthogonal functions, Fourier series; partial differential equations including heat, wave, and Laplace equations. PR: MTH 231. 4 Credit Hours
- Time and Place: 1:00 pm - 1:50 pm MWR at 516 Smith Hall.
- Instructor: Peter Saveliev (call me Peter)
- Office: Smith Hall 713
- Office Hours: MW 2:30 - 5:00, or by appointment
- Office Phone: x4639
- E-mail: saveliev@marshall.edu
- Class Web-Page: math02.com
- Prerequisites: Calculus 1, 2, 3
- Text: optional
- Goals: familiarity with differential equations and some modeling
- Computer Restrictions: graphic calculator TI-83 or TI-83+
- Activities: the student will practice each outcome via the online homework and modeling.
- Evaluation: the student achievement of each outcome will be assessed via
- in-class quizzes
- homework: accessed and graded online, provided by Webwork, http://webwork.marshall.edu/webwork2/S17-Math-335-Saveliev/
- in-class tests
- projects: applications of differential equations
- Grade Breakdown: TOTAL $= .05 \times P + .30\times (Q + H) + .30\times P + .35\times F$
- participation: $5\%$
- quizzes and online homework: $30\%$
- projects: $30\%$
- final exam: $35\% $
For other details, see Course policy.
Lectures
They will appear here as the course progresses.
- Set 1
- Set 2
- Set 3
- Ordinary differential equations, chapter
- Systems of ODEs, chapter
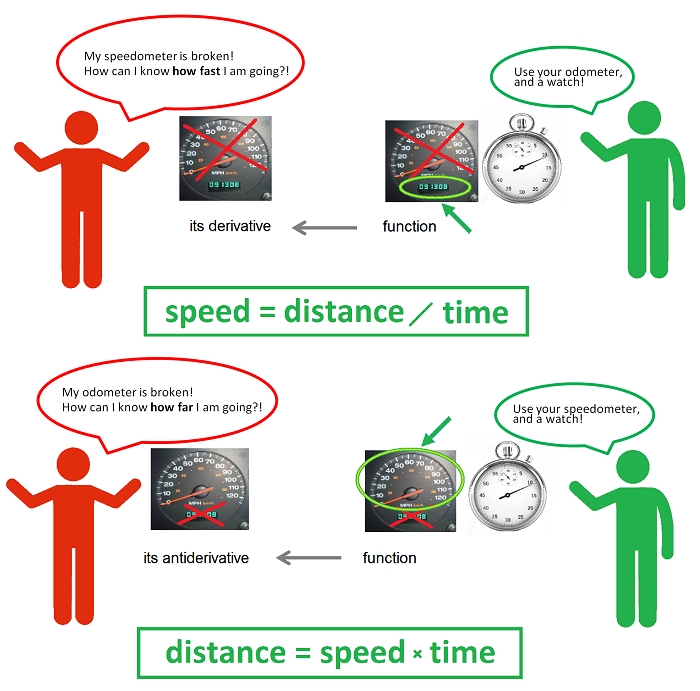
Calculus in one picture...
Computing and modeling
There will be regular modeling assignments and a final project.
Computing assignment #1: Free fall (due Feb 6). Carry out, complete, or reproduce one of these projects from calculus 1 (the output should be a short presentation demonstrating an Excel spreadsheet accompanied by an explanation):
- 1. How do I throw a ball down a staircase so that it bounces off each step? (fall 2016)
- 2. How should you throw a ball from the top of a $100$ story building so that it hits the ground at $100$ feet per second? (fall 2016)
- 3. I would like to use a cannon with a muzzle velocity of $100$ feet per second to bombard the inside of a fortification $300$ feet away with walls $20$ feet high. (fall 2016)
- 4. I have a toy cannon and I want to shoot it from a table and hit a spot on the floor $10$ feet away from the table. (fall 2016)
- 5. How hard do I have to push a toy truck from the floor up a $30$ degree incline to make it reach the top of the table at zero speed? (fall 2016)
- 6. How fast does the shadow of a falling ball on a sliding ladder move?
- 7. How fast do I have to move my hand while spinning a sling in order to throw the rock $100$ feet away? (fall 2016)
Note: The Excel file with the “free fall” equations is here for download, some explanations are here.
Computing assignment #2: Euler's method (due Feb 22). For one of the ODEs below, subject it to Euler's method analysis with Excel:
- Analyze the domain of the right-hand side, apply the theorems about existence and uniqueness.
- Plot sufficiently many solutions.
- Find patterns of the set of solutions, such as: periodicity, monotonicity, asymptotes, symmetry, and any other.
ODEs:
- 1. $y'=\tan (y^2)$;
- 2. $y'=\cos (x+y)$;
- 3. $y'=\cos y \cdot \sqrt{|y|}$;
- 4. $y'=\sin y \cdot \sqrt{ y}$;
- 5. $y'=[x+y]$ (the FLOOR function in Excel);
- 6. $y'=\frac{1}{x-y}$.
Note: The Excel file with the “Euler's method” is here for download.
Computing assignment #3: Euler's method on the plane (due March 8). For one of the systems of ODEs below, perform the same tasks as in the last assignment:
- 1. $x'=\sin y,\ y'=\tan (y^2)$;
- 2. $x'=|y|,\ y'=\cos (x+y)$;
- 3. $x'=x+y,\ y'=\cos y \cdot \sqrt{|y|}$;
- 4. $x'=y,\ y'=\sin y \cdot \sqrt{ y}$;
- 5. $x'=x-y,\ y'=[x+y]$ (the FLOOR function in Excel);
- 6. $x'=\cos(x+y),\ y'=\frac{1}{x-y}$.
Note: The Excel file with the “Euler's method dimension 2” is here for download.
Computing assignment #4: final project, stages 1 and 2 (due April 3).
Final project (due April 23)
The student will be given a short, one or two sentences, description of a problem.
- Stage 1: The student's first task is to ask the right questions in order to recast the problem in the language of the appropriate mathematics.
- Stage 2: Then he is to explore the problem numerically and graphically (with a discrete models and/or Euler's method) with a spreadsheet and make an approximation of what the answer might be and ask further questions.
- Stage 3: Finally, the problem is solved analytically (when possible) with the tools of this course and the answer is confirmed.
All the steps, the explanations of the methods, the data, the illustrations, and the computations are presented in writing. The methods should be based entirely on the material of the course.
The actual project statements may be poorly formulated, incomplete, and have many possible answers or none at all. As a result, the structure of the project might be much more complex than the three stages above.
Instructions:
- Your submission should be both on paper and in a digital format such as PDF (it will be linked here).
- It is a good idea to go digital from the beginning; for example, write with Latex or MS Word, draw with MS Paint, analyze data with MS Excel or Google spreadsheets.
- Include: the name, the title, introduction, conclusions, labeled pictures and tables, references, etc.
Topics:
- 1. How do I throw a ball down an infinite staircase so that it bounces off each step?
- 2. What is the shape of a slide that allows the fastest time down? (spring 2017)
- 3a. How would two tanks with broken turrets battle if they try to shoot at each other at all times?
- 3b. How would two tanks -- one with a broken turret and the other with broken tracks -- battle if they try to shoot at each other at all times? (spring 2017)
- 4a. How would predator and prey populations interact when their dynamics is affected by seasons? (spring 2017)
- 4b. How would predator and prey populations interact when their dynamics is affected by random fluctuation?
- 5. How would a hound pursue a rabbit if it attempted to aim with a lead? (spring 2017)
- 6a. What is the trajectory of the Moon around the Sun? (spring 2017)
- 6b. How do I bring a craft from the Earth's orbit to the Moon's?
- 7a. How does communicable disease spread through a population: some of the susceptible individuals are infected and then removed from the susceptible population, in the seasonal setting?
- 7b. How does communicable disease spread through a population geographically?
- 8. How does a heat-seeking missile pursue an aircraft? (spring 2017)
- 9. How fast does heat propagate through an object when the object also expands when heated?
- 10. Can a sailing boat go in the direction opposite to the direction of the wind?
- 11. Suppose every farmer adjusts the price of the wheat he sells according to the average price of his neighbors. What will happen to the prices?
Exams
- Differential equations -- Spring 2017 -- final exam: Friday May 5, 12:45, same place
The degree to which the old exam will match the current course is limited.
- Sample: Differential equations: test 1
- Sample: Differential equations: test 2
- Sample: Differential equations: final exam