Derivative as a linear operator

Consider integration by substitution

$$\displaystyle\int x e^{x^{2}} dx.$$

Let

$$u = x^2,$$

then with differentiation we get

$du = 2x dx$ (differential form).

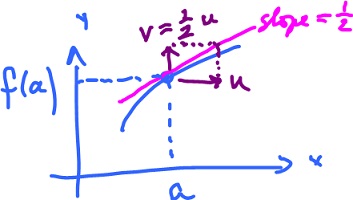
Then, $f'(a): {\bf R} \rightarrow {\bf R}$ is a linear operator, computed by

$$f'(a)(dx) = 2x dx.$$

Understanding the derivative as a linear operator is a stepping stone to a more advanced way of looking at differentiation and integration - via differential forms.

A derivative is a linear map $= 1 \cdot$ form.

Consider

• $\displaystyle\int_1^2 x^2 dx,$
• $\displaystyle\int_1^2 x^2 dx$ Calculus,
• $\displaystyle\int_0^1 x^2 dx$ Differential Geometry, where $x^2 dx$ a differential form, a $1$-form.

Analogously, $\displaystyle\int x^2 dx \hspace{1pt} dy$ is a $2$-form, etc.

Stokes theorem.

$$\displaystyle\int_{\omega} d{\omega} = \displaystyle\int_{\partial} {\omega},$$

where ${\partial}{\omega}$ is the boundary of ${\omega}$.

Let ${\rm dim \hspace{3pt}} = 1, {\omega} = [ a, b ]$

$$\displaystyle\int_a^b f(x) dx = F(b) - F(a),$$

where ${\partial}[ a, b ] = \{ a, b \}$.

In ${\rm dim \hspace{3pt} 2}$ we observe that the boundary of a disk is a circle.

The formula is the same, as long as we now what we integrate, i.e., differential forms.

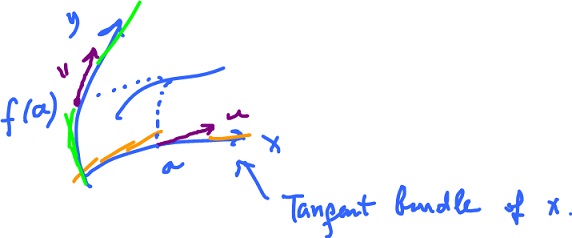
What if the universe is curved?

Then $f′(a)$ is still a linear operator, but from where to where?

$u \in T_a$ tangent to the $x$-axis,
$v \in T_{f(a)}$ tangent to the $y$-axis.

A: between the tangent bundles.

For more see Introduction to differential forms: course.