This site is being phased out.
Continuous functions
Contents
Continuity as preservation of proximity
We are not done with continuity!
Let's review the stages our definition of continuity went through.
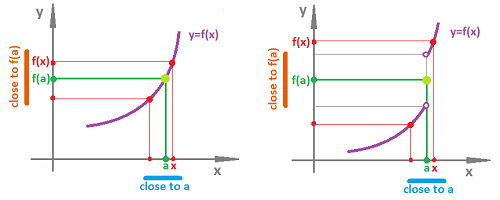
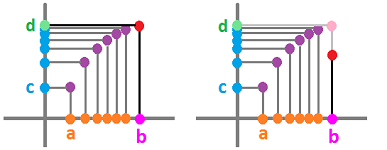
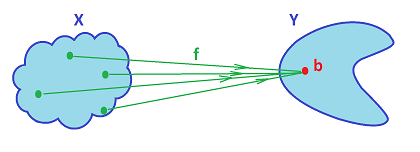
First we, informally, discussed continuity of a function as a transformation that does not tear things apart and interpreted this idea in terms of closeness (proximity) of the input values vs. that of the output values:
Then, this informal idea brought us to the calculus definition of continuity of $f$ at point $x=a$:
and, further, in multidimensional calculus the norm replaced the absolute value:
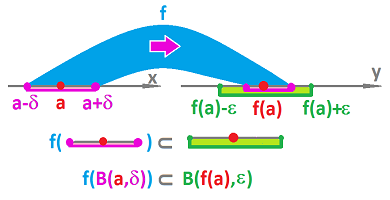
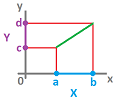
Next we realized that these inequalities are simply inclusions:
where $B(p,d)= \{u :\ ||u-p|| < d \}$ is an open ball in ${\bf R}^n$:
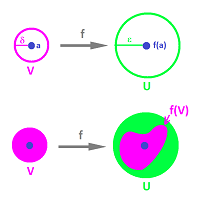
Then, using the simple concept of the image of subset, we re-wrote the definition one more time:
As the last step, we interpreted these Euclidean balls as “neighborhoods” of points, i.e., elements of a basis that generates the topology. In the purely topological setting that we have developed, the definition becomes as follows. Given two sets $X,Y$ with bases of neighborhoods $\gamma_X,\gamma_Y$, a function $f:X\to Y$ is continuous if
We further explore this definition below.
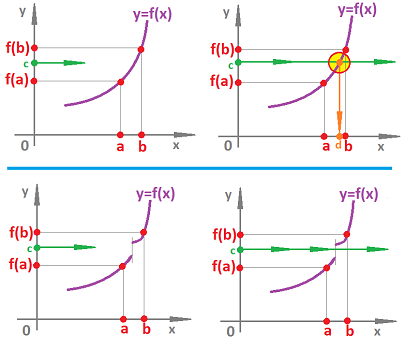
We start with a simple observation that if we replace neighborhoods with open sets in the definition, it would still guarantee that the function is continuous. In fact, the converse is also true.
Theorem. Given two topological spaces $X,Y$, a function $f:X\to Y$ is continuous if and only if
Exercise. Prove the theorem.
Exercise. Demonstrate the relation between our definition and “continuity from the left and right” from calculus.
Continuity and preimages
Using the concept of image has proven to be very beneficial, but the following, related, concept is even more appropriate in this context.
Definition. For any function $f: X \to Y$ the preimage of subset $B \subset Y$ under $f$ is defined to be $$f^{-1}(B) := \{x \colon f(x) \in B \}.$$
This set is defined explicitly and is independent from the existence of the inverse function $f^{-1}$.
To appreciate the difference, consider this diagram of consecutive maps: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{cccccccccc} X &\ra{ f }& Y& \ra{ g }& Z& \ra{ h }&U &\ra{}&... \end{array}$$ Here, we can trace both points and sets in the forward direction: $$x \mapsto y:=f(x) \mapsto z:=g(y) \mapsto u:=h(z) \mapsto ...,$$ $$A \mapsto B:=f(A) \mapsto C:=g(B) \mapsto D:=h(C) \mapsto ...,$$ but, since the preimages of points are sets, we can only follow sets in the reverse direction: $$f^{-1}(T) \leftarrow T:=g^{-1}(R) \leftarrow R:=h^{-1}(S) \leftarrow S...$$
Of course, preimages appear implicitly in many areas of mathematics. For example, the solution set of the equation $f(x) = b$ is $f^{-1}(\{b\})$. In particular, the kernel of a linear operator is the preimage of the zero: $$\ker f=f^{-1}(0).$$
We will now consider the preimage of an open set under a continuous function.
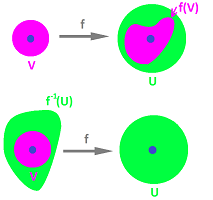
This is actually quite simple: the inclusion $$f(V)\subset U$$ of the definition can now be re-written as $$V\subset f^{-1}(U):$$
The fact that such a $V$ exists for any point in $f^{-1}(U)$ suggests that this set is open.
Theorem. Suppose $f : X \to Y$ is continuous. Then, if $U \subset Y$ is open then so is $f^{-1}(U)$.
Proof. Suppose $U$ is open in $Y$. Let $a \in f^{-1}(U)$ be arbitrary. Let $b := f(a)$. Then $b \in U$. Since $U$ is open, $b$ has a neighborhood $E$ that lies entirely in $U$: $$b \in E \subset U.$$ Now, the last version of the definition of continuity applies: there is a neighborhood $D$ of $a$ such that $f( D ) \subset E$. The last inclusion can be re-written as: $$D \subset f^{-1}(E),$$ and, since $E \subset U$, we have $$D \subset f^{-1}(U).$$ Hence, $f^{-1}(U)$ is open.
$\blacksquare$
Warning: the image of an open set does not have to be open, as the example of a constant function shows.
We've gone far from the original definition of continuity! Let's illustrate the new idea, “preimages of open sets are open”, by trying to think of a function $f$ with
- open range, such as $(c,d)$, but
- closed domain, such as $[a,b]$.
Then one can imagine a scenario: $$d_n \to d \quad\leadsto\quad d_n=f(b_n) \quad\leadsto\quad b_n \to b \quad\leadsto\quad f(b)\ne d.$$ So, the values of $f$ approach $d$ but never reach it, thus exhibiting a familiar discontinuous behavior.
The converse of the theorem is also true:
Theorem. Suppose a function $f : X \to Y$ satisfies: if $U \subset Y$ is open then so is $f^{-1}(U)$. Then $f$ is continuous.
Exercise. Prove the theorem.
Exercise. Prove that $f$ is continuous if and only if the preimage of any closed set is closed.
Exercise. Is the image of a closed set under a continuous function closed?
Exercise. Prove that the image of a closed set under a continuous periodic function from ${\bf R}$ to ${\bf R}$ is closed (i.e., the function is “closed”).
Exercise. Suppose $f:X\to Y$ is continuous. Prove
- for any $A\subset X$, $f(\operatorname{Cl}(A))\subset \operatorname{Cl}(f(A))$, and
- for any $B\subset Y$, $\operatorname{Cl}(f^{-1}(B)) \subset f^{-1}(\operatorname{Cl}(B)).$
Continuous functions everywhere
A typical continuity argument is as follows.
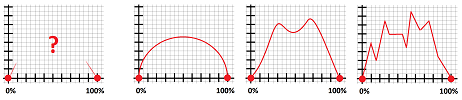
Example (Laffer curve). The exact dependence of the revenue on the tax rate is unknown. It is, however, natural to assume that both $0\%$ and $100\%$ rates will produce zero revenue.
If we also assume that the dependence is continuous, we conclude that increasing the rate may yield decreasing revenue.
$\square$
Exercise. Show that the two hands of a clock will meet at least once a day. What if the clock is malfunctioning?
In our study, we will borrow results from calculus.
First, we have a long list of continuous functions.
Proposition. The following functions are continuous on their domains:
- polynomials;
- rational functions;
- $\sin x, \cos x, \tan x$, and other trigonometric functions;
- $e^x, \ln x$, and other exponential and logarithmic functions.
Second, we know that the four algebraic operation between functions preserve continuity -- within the intersection of their domains -- as follows.
Proposition. If two functions $f:A\to {\bf R},g:B\to {\bf R},\ A,B \subset {\bf R}$, are continuous, then so are
- $f + g :A\cap B\to {\bf R}$;
- $f - g :A\cap B\to {\bf R}$;
- $f \cdot g :A\cap B\to {\bf R}$;
- $f / g :A\cap B \cap \{x:g(x)\ne 0\} \to {\bf R}$.
Exercise. Interpret the proposition in terms of $C[a,b]$ (assume $A:=B:=[a,b]$). These operations make $C[a,b]$ into?...
Third, the compositions of functions preserve continuity, as long as the domains and range match, as follows.
Proposition. If two functions $f:A\to {\bf R},\ g:B\to {\bf R},\ A,B \subset {\bf R}$, are continuous, then so is $gf:A\to {\bf R}$ provided $f(A)\subset B$.
Exercise. Relax the last condition.
Fourth, the minimum and the maximum preserve continuity.
Proposition. If two functions $f,g:X\to {\bf R}$, are continuous, then so are these: $$M(x):=\max \{f(x),g(x)\},\ \ m(x):=\min \{f(x),g(x)\}.$$
Exercise. Prove the proposition.
Fifth, a function of several variables is continuous if and only if it is continuous with respect to each of its variables. And a vector-valued function is continuous if and only if every of its coordinate functions is continuous. And so on.
More advanced calculus results are the following.
Proposition. Evaluation is continuous: for any $c\in [a,b]$ the function $\Psi: C[a,b] \to {\bf R}$ given by $$\Psi (f):= f(c)$$ is continuous.
Proposition. Definite integration is continuous: the function $\Phi:C[a,b]\to {\bf R}$ given by $$\Phi (f):= \int_a^b f(x) dx$$ is continuous.
Exercise. (a) Prove the two propositions -- for the topology of uniform convergence. (b) Consider their analogues for the point-wise convergence. (c) What about anti-differentiation? (d) What about differentiation?
Definition. The graph of a function $f:X\to Y$ is the set $$\operatorname{Graph}(f):=\{(x,y)\in X\times Y:\ y=f(x)\}.$$
Proposition. The graph of a continuous function $f:{\bf R}\to {\bf R}$ is closed in ${\bf R}^2$.
Exercise. Prove the proposition.
Proposition. In case of metric spaces, a function $f:X\to Y$ is continuous if and only if the function commutes with limits: $$\lim_{n\to \infty}f(x_n)=f\left(\lim_{n\to \infty}x_n\right),$$ for any convergent sequence $\{x_n\}$ in $X$.
Exercise. Prove the proposition.
In calculus, the topology is always assumed to be Euclidean. In general, continuity depends on the choice of topology. However, there are functions -- between topological spaces -- that are always continuous.
Terminology. In the context of the above examples, the term commonly used is continuous functions but in topology it is maps. The latter will be used predominantly throughout.
Definition. Suppose we have a topological space $X$, then we can define the identity function $\operatorname{Id}_X: X \to X$ by
Proposition. The identity function is continuous.
Proof. For every open $U$, $$f^{-1}(U) = U$$ is open. $\blacksquare$
Definition. Suppose we have topological spaces $X$ and $Y$, then for any given $b \in Y$, we can define a constant function $f: X \to Y$ by
Proposition. Any constant function is continuous.
Proof. Indeed, suppose $U$ is open in $Y$. Then we have two cases:
- Case 1: $b \in U \Rightarrow f^{-1}(U) = X$, which is open.
- Case 2: $b \in X \setminus U \Rightarrow f^{-1}(U) = \emptyset$, which is open too.
$\blacksquare$
Exercise. Under what circumstances is the function $f:X\to X$ with $f(x)=x$ or $f(x)=c$ for a fixed $c\in X$ continuous?
Exercise. Suppose $X$ is a topological space.
- Suppose $f:X\to {\bf R}$ is continuous. Show that the solution set of any equation with respect to $f$, i.e., $\{x\in X: f(x)=r\}$ for some $r\in {\bf R}$, is closed.
- Show that this conclusion fails for a general continuous $f:X\to Y$, where $Y$ is an arbitrary topological space.
- What condition on $Y$ would guarantee that the conclusion holds?
Continuity isn't synonymous with good behavior.
Example (space filling curve). This curve is build iteratively and we will accept without proof that the limit of these continuous curves is also continuous:
We will later demonstrate however that even such a monstrous function can be slightly “deformed” so that, while still continuous, it isn't onto anymore.
$\square$
Exercise. Given $g_a(x)=x^3-x+a,\ a\in {\bf R}$, let $f(a)$ be the largest root of $g_a$. Is $f$ continuous?
Compositions and path-connectedness
This is our new definition.
Definition. A function $f : X \to Y$ is continuous if for any open $U$, its preimage $f^{-1}(U)$ is also open.
It isn't only much more compact than the original, but also allows us to make some theorems quite transparent.
Theorem. The composition of continuous functions is continuous.
Proof. Suppose we have two continuous functions $f : X \to Y$ and $g : Y \to Z$. Let $h: X \to Z$ be their composition: $h = gf$. Observe first that, in the diagram $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} & X & \ra{f} & Y \\ & _{h=g f} & \searrow & \da{g} \\ & & & Z, \end{array} $$ we can trace back any set $U \subset Z$: $$h^{-1}(U) = (gf)^{-1}(U) = f^{-1}(g^{-1}(U)).$$ Suppose $U$ is open in $Z$. Then $V:=g^{-1}(U)$ is open in $Y$, since $g$ is continuous. Then $W:=f^{-1}(V)$ is open in $X$, since $f$ is continuous. Thus, the set $$h^{-1}(U)=f^{-1}(g^{-1}(U))=f^{-1}(V)=W$$ is open in $X$. Therefore $h$ is continuous.
$\blacksquare$
A proof based on the $\epsilon \delta$-definition is lengthier, even though, in essence, it is exactly the same.
Our original understanding of continuity of functions in calculus was as ones with no gaps in their graphs. It was confirmed (without proof) by the following.
Theorem (Intermediate Value Theorem). Suppose $f :[a,b] \to {\bf R}$ is continuous. Then for any $c$ between $f(a)$ and $f(b)$, there is $d \in [a,b]$ such that $f(d) = c$.
We are ready to prove it now, in a more general context.
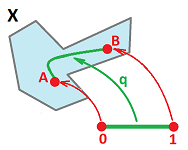
Recall the definition: a topological space $Q$ is path-connected if for any $A, B \in Q$ there is a continuous function $p: [ 0, 1 ] \to Q$ such that $$p(0) = A \text{ and } p(1) = B.$$
Exercise. Prove first that $[a,b]$ is path-connected, and so are $(a,b),[a,b)$.
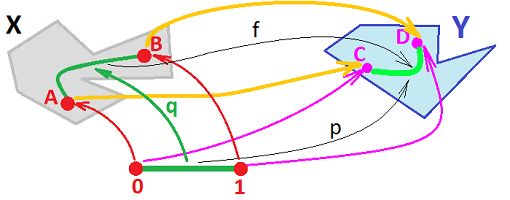
Theorem. Path-connectedness is preserved by continuous functions: if $f :X \to Y$ is continuous and onto, then if $X$ is path-connected then so is $Y$.
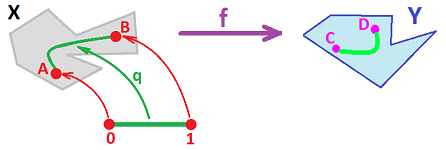
Proof. The idea is to re-state the problem of finding the necessary path in $Y$ as a problem of finding a certain path in $X$:
Then, the problem of finding a path from $A$ to $B$ can be solved in $X$. However, we are facing the problem of finding a path from $C$ to $D$ in $Y$ instead! Where would it come from? The answer is, from $X$ via $f$.
Since $f$ is onto, every point is $Y$ comes from $X$, so there are $A,B\in X$ such that $$C = f(A), \ D = f(B).$$
We then use the path-connectedness of $X$ and find a continuous function $$q : [ 0, 1 ] \to X$$ such that $$q (0) = A,\ q (1) = B.$$ Now let $$p := f q.$$
Thus,
- 1. $p$ is continuous as the composition of two continuous functions (last theorem),
- 2. $p(0) = f ( q (0) ) = f( A) = C$,
- 3. $p(1) = f ( q (1) ) = f( B ) = D.$
Therefore, function $p$ satisfies the above definition.
$\blacksquare$
The proof is summarized in this commutative diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} & [0,1] & \ra{q} & X \\ & _{p=fq} & \searrow & \da{f} \\ & & & Y. \end{array} $$
Exercise. Derive the Intermediate Value Theorem from the last theorem.
Exercise. A topological space is called connected if it can't be represented as a disjoint union of two closed sets. Prove that every path-connected space is connected.
Categories
The results we have proven about topological spaces and continuous functions, especially the one about the composition, have a far-reaching generalization.
A category ${\mathscr C}$ consists of
- a collection $\operatorname{Obj}({\mathscr C})$ of objects;
- a collection $\operatorname{Hom}({\mathscr C})$ of morphisms between some pairs of objects.
Morphisms are also called arrows, which emphasizes the point that they are not functions just as the objects aren't sets.
Each morphism $f$ has unique source object $X \in \operatorname{Obj}({\mathscr C})$ and target object $Y\in \operatorname{Obj}({\mathscr C})$. We write then $f: X \to Y$.
Then the category as a whole can be illustrated by this diagram: $$ \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % {\mathscr C}=\left\{ \begin{array}{cccccccc} &X & \in \operatorname{Obj}({\mathscr C})\\ &\ \da{f} & \in \operatorname{Hom}({\mathscr C})\\ &Y & \in \operatorname{Obj}({\mathscr C}) \end{array} \right\} $$ We write $\operatorname{Hom}_{\mathscr C}(X,Y)$ (or simply $\text{Hom}(X,Y)$ when there is no confusion about to which category it refers) to denote the class of all morphisms from $X$ to $Y$.
Suppose we have three objects $X,Y,Z \in \operatorname{Obj}({\mathscr C})$. Then for any two morphisms $f : X \to Y$ and $g : Y \to Z$, there is a third called their composition written as $gf: X \to Z$. The composition completes the following commutative diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{cccccccc} &X & \ra{f} & Y & \\ & & _{gf}\ddots & \ \da{g} & \\ & & & Z & \end{array} $$
We assume that the following axioms hold:
- identity: for every object $X \in \operatorname{Obj}({\mathscr C})$, there exists a morphism $\operatorname{Id}_X \in \operatorname{Hom}_{\mathscr C}(X,X)$, called the identity morphism for $X$, such that for every morphism $f : X \to Y$, we have
$$\operatorname{Id}_Y f = f = f\operatorname{Id}_X.$$
- associativity: if $f : X \to Y, g : Y \to Z$ and $h : Z \to W$ then $h(gf) = (hg)f$, and
The axioms can be illustrated with diagrams. For the former, it's simply this: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{cccccccc} & X & \ra{f} & Y \quad\quad\quad & X & \ra{f} & Y \\ & & _{f}\searrow & \quad \ \da{\operatorname{Id}_Y} \quad\quad\quad &\quad \ \da{\operatorname{Id}_X} & _{f} \nearrow & \\ & & & Y \quad\quad\quad & X & & & \end{array} $$ For the latter, it's a commutative diagram of commutative diagrams: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{cccccccc} &X & \ra{f} & Y & & X & & Y \\ & & & \ \da{g} & \Rightarrow & & _{gf}\searrow & \\ &W & \la{h} & Z & & W & \la{h} & Z \\ \\ & & \Downarrow & & & & \Downarrow & \\ \\ &X & \ra{f} & Y & & X & & Y \\ & & _{hg}\swarrow & & \Rightarrow & \quad \ \da{hgf} & & \\ &W & & Z & & W & & Z \end{array} $$
The axioms justify the illustration below:
Exercise. Prove that these are categories with morphisms as indicated:
- sets with functions,
- topological spaces with continuous functions,
- groups with group homomorphisms,
- rings with ring homomorphisms,
- vector spaces with linear operators,
- graphs with graph maps.
Exercise. Prove that there is exactly one identity morphism for every object.
Exercise. Define isomorphisms on a category in such a way that it includes homeomorphisms and groups isomorphisms.
The axioms appear similar to those of groups. Indeed, the composition is a binary operation: $$\operatorname{Hom}_{\mathscr C}(X, Y) \times \operatorname{Hom}_{\mathscr C}(Y, Z) \to \operatorname{Hom}_{\mathscr C}(X,Z).$$ However, morphisms don't have to produce a binary operation on the whole $\operatorname{Hom}({\mathscr C})$ since not all compositions may be possible. The reverse connection is valid though as this example of a category ${\mathscr C}$ produced from a group $(G,*)$ shows:
- $\operatorname{Obj}({\mathscr C})=\{*\},$
- $\operatorname{Hom}({\mathscr C})=G.$
Exercise. Prove that this is a category.
Vector fields
Let's recall how we describe motion.
We take as a model a fluid flow. The phase space $S\subset {\bf R}^n$ of the system is the space of all possible locations. Then the position of a given particle is a function $x:I\to S$ of time $t$, where $I$ is some interval. Meanwhile, the dynamics of the particle is governed by the velocity of the flow, at each location and each moment of time. Let $f:[0,\infty)\times S\to {\bf R}^n$ be a function and the velocity at time $t$ of a particle, if it happens to be at point $x$, is $f(t,x)$.
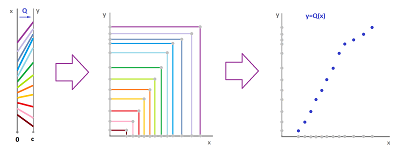
Let's start with dimension $1$ and $S:={\bf R}$. Then this dynamics is given by an ordinary differential equation (ODE): $$x'(t)=f(t,x(t)),$$ Suppose we have such a system in ${\bf R}$. Now, suppose we are given a current state $a$ and a forward propagation time $t$. The by following what's, in essence, the Euler method, we define the forward propagation map that approximates the solution of the ODE: $$Q_t(a)=a+tf(a).$$
In dimension $2$, we are talking about vector fields.
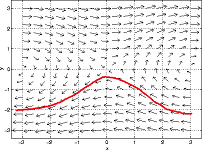
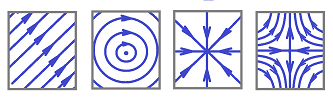
A vector field is given when there is a vector attached to each point of the plane: $${\rm point} \mapsto {\rm vector}.$$ So, vector field is just a function $$V : {\bf R}^2 \to {\bf R}^2 .$$ For example, the following vector field $$V=(f_x,f_y)$$ could be the velocity field of a flow:
One can think of vector fields as systems of time-independent ODEs: $$x'(t)=f_x(x(t),y(t)),$$ $$y'(t)=f_y(x(t),y(t)).$$ This is still a model for a flow: $u=(x,y)$ is the position of a given particle as a function of time $t$ and $(f_x(x,y),f_y(x,y))$ is the velocity of this particle (or any other) if it happens to be at point $(x,y)$.
For any vector field in ${\bf R}^n$, the forward propagation map $$Q_t:{\bf R}^n\to {\bf R}^n$$ is defined by the same formula $$Q_t(a)=a+tV(a).$$ This map is then studied to discover the behavior of the system: stationary points, periodicity, etc.:
Theorem. If $V$ is continuous, the forward propagation map $Q_t:{\bf R}^n\to {\bf R}^n$ is continuous too, for each $t$.
Exercise. Prove this theorem.
The dynamics of a market economy
Suppose we have a “closed” market with $n$ commodities freely traded. The possible prices, $$p_1,...,p_n,$$ of these commodities form a price vector, $$p=(p_1,...,p_n),$$ at each moment of time. Then, the space of prices is $$P:={\bf R}_+^{n+1}:=\{ (p_1,...,p_n):\ p_i\in {\bf R}_+ \}\subset {\bf R}^{n}.$$
Suppose also that there are $m$ “agents” in the market, each owning a certain amount of each commodity. We suppose that
- $i$th agent owns $c_j^i$ of $j$th commodity.
These amounts form the $i$th commodity vector, $$c^i \in {\bf R}_+^n.$$ Then the $i$th agent's wealth is $$w^i=\langle p,c^i \rangle ,$$ where $\langle , \rangle$ is the dot product (we place the price first to emphasize the fact that it is a function of the commodity). We suppose also that this agent wants to own a different combination of commodities. This vector, $d^i$, constitutes the demand of this agent. The demand, of course, depends on the current prices $p$.
One can argue now that the demand function $d^i=d^i(p)$ is continuous. The argument is based on the idea that the demand is elastic enough so that a small change in the price of a commodity will produce a small change in the person's demand for this commodity, as well as other commodities. Even though one-time purchases may require a certain threshold to be reached to become affordable, we argue that approaching this threshold is accompanied by an increase of the likelihood of the purchase. In other words, the person's desire for a certain commodity is unchanged but the affordability does change -- continuously -- with his wealth $w^i=\langle p,c^i \rangle$ as the price vector $p$ changes.
It follows that the market-wide demand function $d=\Sigma _i d^i$ is continuous too. Now, the continuous demand will have a continuous effect on the prices.
Next, let's examine the dynamics of prices.
First, we assume that the tomorrow's prices depend only on the today's prices. We need to justify this assumption. First, we think of the market as truly “closed” so that there is no outside influence on the prices by non-market events, such as wars, natural disasters, new laws and regulations etc. We can simply think that the time gap is so short that these events don't affect the prices. At the same time, we have to think that the time gap is long enough for the information about price changes to disseminate to all participants. In addition, we assume that the prices don't depend on time -- of the day, week, or year.
This dependence, then, is a price function $F:P\to P$. And the analysis above suggests that this dependence is continuous.
Exercise. What difference would price controls have?
What about the commodities? The total amount is the vector $$\bar{c}:=\sum_i c^i \in {\bf R}_+^n.$$ It may be fixed or, assuming continuous production and continuous consumption, it varies continuously. If we also assume that the trading is also continuous, we conclude that the commodity vectors $c^i,\ i=1,2,...,m$, vary continuously as well. Then the dynamics is captured by a continuous function $$G:C\to C,$$ where $$C:=\{(c^1,...,c^m):\ c^i\in {\bf R}_+^n\} = \left( {\bf R}_+^n \right)^m,$$ is the space of distributions of commodities.
The state of the system is then a combination of the prices and a distribution of the commodities. Then the state space is $$S:=P\times C,$$ and the state dynamics is given by a continuous function $D:S\to S$. In other words, tomorrow's prices and distributions are determined by today's prices and distributions.
One can easily incorporate other quantities into this extremely oversimplified model. For example, suppose the interest rates are to be included as they influence and are being influenced by the prices. Then the state space becomes $P\times C\times [0,\infty)$. Any new quantity can be added to this model by simply extending $P$ in this fashion.
This is an example of a more abstract way to model motion and dynamics. It is a discrete dynamical system, which is simply any continuous function $F:P \to P$ on any topological space $P$, applied repeatedly: $$x_{n+1}=F(x_n).$$
Dynamical systems are known for exhibiting a complex behavior even with a simple choice of $F$. Modelling is uncomplicated for dimension $1$; one can simply use a calculator. Just enter a function and then repeatedly apply it. A spreadsheet will allow to visualize the dynamics for dimensions $1$ and $2$.
Exercise. Try $f(x)=rx(1-x)$ for $r=.5,1,2,3.3,3.5,4$. It is called the logistic map.
Maps
We know that path-connectedness is preserved under continuous transformations, which means that we can't tear things!
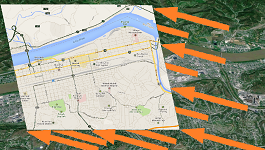
That's the reason why continuous functions are also called maps or mappings. After all, mapping is a process of transferring the terrain -- point by point -- to a piece of paper, a map.
This process should better be continuous!
What if it's not? Then we won't be able to answer the most basic question maps are intended to answer:
The simplest case is when the map itself is torn:
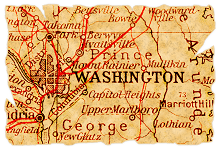
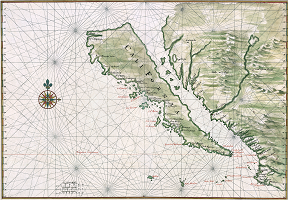
Such a “discontinuous” map might give the answer “No” while, in fact, the terrain it came from answers “Yes”. A more subtle case is when the actual process of mapping was erroneous, such as when a peninsula is turned into an island:
The continuity of the mapping prevents it from tearing the map and guarantees the correct “No”. However, even though we can't tear the map, we might still end up gluing its pieces. A “glued” map might give the answer “Yes” to our question while, in fact, the terrain it is supposed to depict answers “No”. If the process of mapping was erroneous, one might glue -- by mistake -- islands together, or even continents:
Example. Consider these two examples of gluing. First, merging two points: $$f:\{A,B\}\to \{C\},\ f(A)=f(B)=C,$$ and, second, parametrization of the circle: $$f:[0,2\pi]\to {\bf S}^1\subset {\bf R}^2,\ f(t)=(\cos t,\sin t).$$ $\square$
Exercise. Prove that these are continuous functions.
Thus, while a continuous map can't bring the number of components up, it can bring it down.
It turns out, sometimes gluing is bad even though it is a continuous operation. The reason is that the inverse of gluing is tearing!
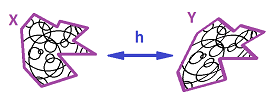
That's why we will define a class of maps so that both the function $$f: X \to Y $$ and its inverse $$f^{-1}: Y \to X$$ are continuous.
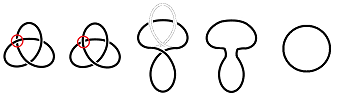
Even though tearing isn't allowed, we can cut -- if you glue it back together exactly as before. For example, this is how you can un-knot this knot:
One can achieve this without cutting by manipulating the knot in the $4$-dimensional space.
Exercise. What is this, topologically?
Homeomorphisms
Let's make this idea more precise. Recall a couple of definitions.
A function $f: X \to Y$ is called one-to-one, or injective, if $$f(x) = f(y) \Rightarrow x = y.$$ Or, the preimage of a point, if non-empty, is a point.
A function $f: X \to Y$ is called onto, or surjective, if
Or, the image of the domain space is the whole target space, $f(X) = Y$.
A function that is one-to-one and onto is also called bijective.
Theorem. A bijective function $f:X \to Y$ has the inverse: there is a unique function $f^{-1}: Y \to X$ such that $f^{-1}f = \operatorname{Id}_X$ and $ff^{-1} = \operatorname{Id}_Y$.
Definition. Suppose $X$ and $Y$ are topological spaces and $f:X \to Y$ is a function. Then, $f$ is called a homeomorphism if
- $f$ is bijective,
- $f$ is continuous
- $f^{-1}$ is continuous.
Then $X$ and $Y$ are said to be homeomorphic, as well as topologically equivalent.
The word “homeomorphism” comes from the Greek words “homoios” for “similar” and “morphē” for “shape” or “form”. One may understand the meaning of this word as follows: the shapes of two geometric objects are similar by being topologically identical.
Let's examine informally how the definition may be applied to demonstrate that spaces are not homeomorphic.
Consider $X$ a segment and $Y$ two segments. We already know that the number of path-components is supposed to be preserved. Therefore, these two are not homeomorphic.
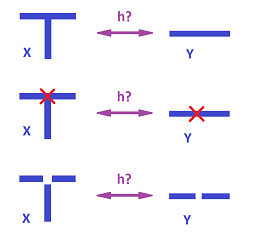
Consider now $X$ letter “T” and $Y$ a segment. Both are path-connected so this information doesn't help. The question remains, are they homeomorphic? One trick is to pick a point $a$ in $X$, remove it, and see if $X\setminus\{a\}$ is homeomorphic to $Y\setminus \{b\}$ for any $b\in Y$. Let's choose $a$ to be in the cross of “T”:
Removing this point creates a mismatch of components regardless what $b$ is.
Then, the method is to examine how many components can be produced by removing various points from the space.
Exercise. Using just this approach classify the symbols of the standard computer keyboard (think of them as if made of wire):
- ` 1 2 3 4 5 6 7 8 9 0 - =
- q w e r t y u i o p [ ] \
- a s d f g h j k l ; '
- z x c v b n m , . /
and
- $\sim \hspace{2 mm} ! \hspace{2 mm} @ \hspace{2 mm} \# \hspace{2 mm}\$ \hspace{2 mm}\% \hspace{2 mm}\hspace{2 mm}\widehat{ } \hspace{2 mm}\& \hspace{2 mm}* \hspace{2 mm}( \hspace{2 mm}) \hspace{2 mm}\_ \hspace{2 mm}+$
- Q W E R T Y U I O P $\{ \}$ |
- A S D F G H J K L : “
- Z X C V B N M < > ?
More general is this almost trivial fact.
Proposition. If spaces $X$ and $Y$ are homeomorphic, then for any $a\in X$ there is $b\in Y$ such that $X \setminus \{a\}$ is homeomorphic to $Y \setminus \{b\}$.
Exercise. Prove the proposition. Suggest an example when counting components, as we did above, isn't sufficient, but the proposition still helps.
Exercise. Prove that an isometry, i.e., a bijection between two metric spaces, that preserves the distance is a homeomorphism.
Example (non-example). It might be hard to quickly come up with an example of a continuous bijection that isn't a homeomorphism. The reason is that our intuition takes us to Euclidean topology. Instead, consider the identity function $$f=\operatorname{Id}:(X,\tau) \to (X,\kappa),$$ where $\kappa$ is the anti-discrete topology and $\tau$ isn't. Then, on the one hand,
- $f^{-1}(X)=X$ is open in $(X,\tau)$,
so that $f$ is continuous. On the other hand, there is a proper subset $A$ of $X$ open in $\tau$, but
- $f(A)=A$ isn't open in $(X,\kappa)$
Therefore, $f^{-1}:(X,\kappa)\to (X,\tau)$ isn't continuous. A specific example is:
- $X=\{a,b\},$
- $\tau=\{\emptyset,\{a\},\{b\},X\},$
- $\kappa=\{\emptyset,\{a\},X\}.$
This example suggests a conclusion: the identity function will be a desired example when $\kappa$ is a proper subset of $\tau$. Consider, for example, $X={\bf R}$, while $\tau$ is the Euclidean topology and $\kappa$ any topology with fewer open sets (it's “sparser”), such as the topology of rays.
$\square$
Exercise. Provide another non-example, a continuous bijection $f:X\to Y$ that isn't a homeomorphism; this time both $X$ and $Y$ are subspaces of ${\bf R}^2$.
Exercise. We are given a continuous function $f:{\bf R}\to {\bf R}$. Define a function $g:{\bf R}\to {\bf R}^2$ by $g(x)=(x,f(x))$. Prove that $g$ is continuous and that its image, the graph of $f$, is homeomorphic to ${\bf R}$.
Exercise. To what is the Mobius band with the center line cut out homeomorphic?
Examples of homeomorphic spaces
Theorem. Closed intervals of non-zero, finite length are homeomorphic.
Proof. Let $X = [a,b], Y = [c,d], \ b>a, d>c$. We will find a function $f: [a,b] \to [c,d]$ with $f(a) = c$ and $f(b) = d$. The simplest function of this kind is linear:
To find the formula, use the point-slope formula from calculus. The line passes through the points $(a,c)$ and $(b,d)$, so its slope is $m = \frac{d-c}{b-a}\ne 0$. Hence, the line is given by $$f(x) = c + m(x-a).$$ We can also give the inverse explicitly: $$f^{-1}(y) = a + \frac{1}{m} \cdot (y-b).$$ Finally we recall that linear functions are continuous.
$\blacksquare$
Theorem. Open intervals of finite length are homeomorphic.
Exercise. Prove the theorem.
Theorem. An open interval is not homeomorphic to a closed interval (nor half-open).
Exercise. Prove the theorem. Hint: remove the end-point.
No interval of non-zero length can be homeomorphic to a point because there can't be a bijective function between them.
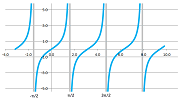
Theorem. All open intervals, even infinite ones, are homeomorphic.
Proof. The tangent gives you a homeomorphism between $(- \pi /2, \pi /2)$ and $(- \infty , \infty )$.
$\blacksquare$
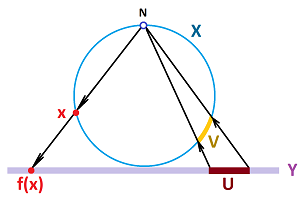
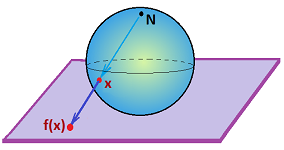
Example (stereographic projection). Another way to justify this conclusion is given by the following construction:
Here the “north pole” $N$ is taken out from a circle to form $X$. Then $X$ is homeomorphic to a finite open interval, and to an infinite interval, $Y$. The function $f:X \to Y$ is defined as follows:
- given $x \in X$, draw a line through $x$ and $N$, find its intersection $y$ with $Y$, then let $y:= f(x)$.
$\square$
Exercise. Prove that this $f$ is a homeomorphism.
The above construction is a $2$-dimensional version of what is, literally, a map:
This construction is used to prove that the sphere with a pinched point is homeomorphic to the plane.
In the $n$-dimensional case, we place ${\bf S}^n$ in ${\bf R}^{n+1}$ as the unit “sphere”: $${\bf S}^n=\{x\in {\bf R}^{n+1}:\ ||x||=1\},$$ and then remove the north pole $N=(0,0,...,0,1)$. The stereographic projection $$P:{\bf S}^n \setminus {N} \to {\bf R}^{n}$$ is defined by $$P(x):=\left( \frac{x_1}{1-x_{n+1}}, \frac{x_2}{1-x_{n+1}},...,\frac{x_n}{1-x_{n+1}} \right), \ \forall x=(x_1,...x_{n+1}).$$ Its inverse is $$P^{-1}(y)=\frac{1}{1+||y||}(2y_1,2y_2,...,2y_n,||y||^2-1), \ \forall y=(y_1,...y_{n}).$$
Exercise. Prove that this is a homeomorphism.
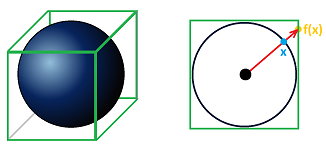
Exercise. Show that the sphere and the hollow cube are homeomorphic. Hint: imagine inserting a balloon inside a box and then inflating it so that it fills the box from the inside:
We can instead concentrate on the inverse of $f$. Let's illustrate the idea in dimension $2$, i.e., square $Y$ and circle $X$. One can give an explicit representation of the function: $$f^{-1}(u) = \frac{u}{||u||},$$ where $||u||$ is the norm of $u$. This function is essentially a radial projection.
Exercise. Prove that $f^{-1}$ is continuous.
Exercise. Let $a,b$ be two distinct points on the sphere $X={\bf S}^2$. Find a homeomorphism of the sphere to itself that takes $a$ to $b$. What if $X$ is the plane, or the torus?
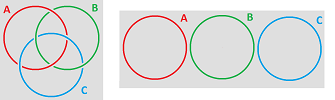
Exercise. Are these two spaces, $A\sqcup B\sqcup C$, homeomorphic?
Topological equivalence
Theorem. Homeomorphisms establishes an equivalence relation on the set of all topological spaces.
Exercise. Prove the theorem.
Then it makes sense to call two spaces topologically equivalent if they are homeomorphic. We will use the following notation for that: $$X \approx Y.$$
There is more to this equivalence... Suppose $$f:(X,\tau_X)\to(Y,\tau_Y)$$ is a homeomorphism. From the definition,
- if $U$ is open in $Y$ then $f^{-1}(U)$ is open in $X$, and
- if $V$ is open in $X$ then $f(V)$ is open in $Y$.
In other words, $$V \in \tau_X \Leftrightarrow f(V)\in \tau _Y.$$ Therefore, we can define a function between the two topologies, as sets of open sets: $$f_{\tau}:\tau_X\to\tau_Y,$$ by setting $$f_{\tau}(V):=f(V).$$ It is a bijection!
The result is that whatever is happening, topologically, in $X$ has an exact counterpart in $Y$: open and closed sets, their unions and intersections, the exterior, interior, closure of sets, and convergent and divergent sequences, continuous and discontinuous functions, etc. To put it informally,
The situation is similar to that in algebra when isomorphic groups (or vector spaces) have the exact matching of every algebraic operation and, in that sense, they are algebraically indistinguishable.
Exercise. Prove that the classes of homeomorphic spaces form a category.
This idea justifies the common language about topological spaces that is often appropriate:
This is the reason why we speak of some classes of homeomorphic spaces as if they are represented by specific topological spaces:
- the circle ${\bf S}^1$,
- the disk ${\bf B}^2$,
- the sphere ${\bf S}^2$,
- the torus ${\bf T}^2$, etc.
The attitude is similar to that of algebra: a group is ${\bf Z}, {\bf Z}_p, \mathcal{S}_n$, etc. (Also, “the lion” refers to all the lions as a species, etc.)
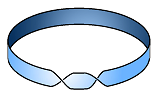
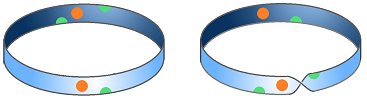
It would be dangerous to apply this idea to bases instead of topologies. Indeed, the bases of this cylinder and the Mobius band may seem indistinguishable but the spaces aren't homeomorphic:
Properties “preserved” under homeomorphisms are called topological invariants.
Exercise. Prove that the “number of points (including infinity)” is a topological invariant.
In anticipation of our future studies we mention that the homology groups of homeomorphic spaces are isomorphic. In other words, homology is a topological invariant. However, the converse isn't true. Indeed, even though a point and a segment aren't homeomorphic, their homology groups coincide.
Exercise. Prove that for a given topological space, the set of all of its self-homeomorphisms form a group with respect to composition.