This site is being phased out.
Continuity of functions
Contents
Definition
Recall the definition.
Definition. $$ \lim_{x \to a} f(x) = f(a) $$
Now graphically, what is the mathematical idea of continuity? A continuous function should have a "continuous" graph, i.e. one made up of one piece. What does this have to do with $\lim\limits_{x \to a} f(x) = f(a)$? The limit tells us that there is no cut of the graph at $x=a$.
Let's consider this in detail. Given a point $a$ and a function $f$, we have three non-overlapping pieces:
- Graph of $f$ restricted to $(-\infty, a)$.
- The point $(a, f(a))$.
- The graph restricted to $(a,\infty)$.
To have a single piece, we want them together:
Algebraically, $$\underbrace{\left.\begin{aligned} \lim_{x \to a^{-}} f(x) = f(a) \\ \lim_{x \to a^{+}} f(x) = f(a) \end{aligned}\right\}}_{\text{Use this to prove continuity.}} \quad \Rightarrow \quad \underbrace{\lim_{x\to a} f(x) = f(a)}_{f \text{ is continuous at } x=a} $$
Example. $$f(x) = \begin{cases} x + 1 & \text{ if } x < 0 \\ e^{x} & \text{ if } 0 \leq x \leq 1 \\ 2 - x & \text{ if } x > 1 \end{cases} $$ Find the values for which $f$ is discontinuous, i.e. classify all $x=a$ in this respect.
Consider the three main pieces:
- $(\infty , 0)$, $f(x)$ is linear, so $f$ is continuous at each $a<0$.
- $(0,1)$, $f(x)$ is exponential, so $f$ is continuous at each $0 < a < 1$.
- $(1,\infty)$, $f$ is linear, so $f$ is continuous at each $a > 1$.
Left are the values of 0 and 1:
$a = 0$:
$$\begin{aligned}
\lim_{x \to 0^{-}} & = \lim_{x \to 0^{-}}(x + 1) = 0 + 1 = 1 \\
\lim_{x \to 0^{+}} & = \lim_{x \to 0^{+}}e^{x} = e^{0} = 1
\end{aligned}$$
So $f$ is continuous at $x=0$ because the limit of both equal to $1$ and the value of $f(0)=1$.
$a = 1$: $$\begin{aligned} \lim_{x \to 1^{-}} & = \lim_{x \to 1^{-}}e^{x} = e^{1} = e \\ \lim_{x \to 1^{+}} & = \lim_{x \to 1^{+}}(2-x) = 2-1 = 1 \end{aligned}$$ Mismatch! Since $e \neq 1$, the two one-sided limits are unequal (the branches are misaligned). So by definition, $f$ is discontinuous at $1$.
Classification of discontinuities
Jump discontinuity
The function has a jump discontinuity at $x=a$ when $\lim\limits_{x \to a^{-}} f(x)$ and $\lim\limits_{x \to a^{+}} f(x)$ exist but is not equal to each other.
Removable discontinuity
The function has a removable discontinuity at $x=a$ when $\lim\limits_{x\to a^{-}} f(x)$ and $\lim\limits_{x\to a^{+}} f(x)$ exist and equal to each other but not equal to $f(a)$.
Example. $$\frac{x^{2} - 1}{x+1}, \qquad a = 1$$
Infinite discontinuity
The function has an infinite discontinuity at $x=a$ when one or both of $\lim\limits_{x\to a^{-}} f(x)$, $\lim\limits_{x\to a^{+}} f(x)$ is infinite.
More severe discontinuities When one (or both) of the limits does not exist (as a number) or as infinity.
Example.
$$\sin \frac{1}{x}$$ at $x=0$
Example. $$f(x) = x\sin \frac{1}{x}$$ at $x=0$
Is it continuous at $x=0$? No, because $f(0)$ is undefined. But this is a removable discontinuity.
So far we have discussed continuity at $x=a$, i.e., one point at a time. Now, $f$ is continuous on interval $I$ if $f$ is continuous at every $a$ in $I$.
Above example (piecewise defined function). The answer was: "Discountinuous at $x=1$" only.
Restate as: $f$ is continuous on $(-\infty,1)$ and $(1,\infty)$.
We say $f$ is a continuous function if $f$ is continuous on $(-\infty,\infty)$.
Review
Continuous functions:
- $\sin$, $\cos$
- Linear, quadratic, polynomial, etc. functions.
- Exponential functions.
Continuous on their domains:
Other. The square root $\sqrt{x}$ is defined but not continuous at $x=0$.
Because $\lim\limits_{x\to 0} \sqrt{x}$ does not exist but $\lim\limits_{x \to o^{+}} \sqrt{x}$ exists and equal to $0=\sqrt{0} = f(0)$.
Special types of continuity
Definition. We say $f$ is continuous from the right at $a$ if $$\lim_{x \to a^{+}} f(x) = f(a). $$ We sat $f$ is continuous from the left at $a$ if $$\lim_{x \to a^{-}} f(x) = f(a). $$
Then
continuous left + right = continuous.
Continuity and algebra
What happens to continuous functions when we combine them algebraically?
$f+g$
If $f$ and $g$ are continuous, then so is $f+g$?
Yes, why?
Informally, the shift, $g(x)$, of the graph of $f$ is uniformly distributed, so it won't break the graph of $f$.
More precisely, show: $$\lim_{x \to a} \left(f(x) + g(x)\right) = f(a) + g(a) $$ How?
This is what we know: $$\begin{aligned} \lim_{x \to a} f(x) &= f(a) \\ \lim_{x \to a} g(x) &= g(a) \end{aligned}$$ Based on the Sum Rule of Limits.
We have $f$ and $g$ continuous at $x=a$, so by definition
- $\lim\limits_{x\to a} f(x) = f(a)$ and
- $\lim\limits_{x\to a} g(x) = g(a)$.
Then to show that $f+g$ is continuous at $x = a$, consider $$\begin{aligned} \lim_{x \to a}(f + g)(x) &= \lim_{x \to a}\left(f(x) + g(x)\right) \\ &= \lim_{x \to a} f(x) + \lim_{x \to a} g(x) \\ &= f(a) + g(a) &= (f + g)(a) \end{aligned}$$ So by definition, $f+g$ is continuous at $a$.
$f-g$
To show that $f-g$ is continuous at $x = a$, consider $$\begin{aligned} \lim_{x \to a}(f - g)(x) &= \lim_{x \to a}\left(f(x) - g(x)\right) \\ &= \lim_{x \to a} f(x) - \lim_{x \to a} g(x) \\ &= f(a) - g(a) &= (f - g)(a) \end{aligned}$$ So by definition, $f-g$ is continuous at $a$.
$f\cdot g$
To show that $f\cdot g$ is continuous at $x = a$, consider $$\begin{aligned} \lim_{x \to a}(f \cdot g)(x) &= \lim_{x \to a}\left(f(x) \cdot g(x)\right) \\ &= \lim_{x \to a} f(x) \cdot \lim_{x \to a} g(x) \\ &= f(a) \cdot g(a) &= (f \cdot g)(a) \end{aligned}$$ So by definition, $f\cdot g$ is continuous at $a$.
$f/g$ To show that $f/g$ is continuous at $x = a$, consider $$\begin{aligned} \lim_{x \to a}(f / g)(x) &= \lim_{x \to a}\left(\frac{f(x)}{g(x)}\right) \\ &= \frac{\lim\limits_{x \to a} f(x)}{\lim\limits_{x \to a} g(x)} \\ &= \frac{f(a)}{g(a)} \\ &= \left(\frac{f}{g}\right)(a) \end{aligned}$$ So by definition, $f\cdot g$ is continuous at $a$.
Example. Consider these functions: $f(x) = 1, \qquad g(x) = x$. They are continuous for all $x$.
Let $h(x) = \frac{f(x)}{g(x)}$ is continuous at $x=a$ provided $\lim\limits_{x \to a} g(x) \neq 0$, or $g(a) \neq 0$, $x \neq 0$.
$\text{QR} \Rightarrow \frac{1}{x}$ is continuous for all $x$ except 0.
To summarize...
Theorem. If $f\cdot g$ are continuous at $x=a$, then so are
- $f+g$,
- $f-g$,
- $f\cdot g$, and
- $f/g$ provided $g(a) \neq 0$.
More algebra
Isn't there one more algebraic operation?
Yes, the composition.
Recall:
- Substitution Rule
- If $f$ is continuous at $y = \lim\limits_{x \to a} g(x)$ then $$\underbrace{\lim_{x \to a} f(g(x))}_{\text{Simplification, limit of composition of two functions.}} = f(\underbrace{\lim_{x\to a} g(x)}_{\text{Limit of } g \text{ only}}) $$
Compare to: $$ \lim_{x \to a} \left( f(x) + g(x) \right) = \lim_{x \to a} f(x) + \lim_{x \to a} g(x) $$
Assume, in addition, that $g$ is continuous at $x=a$, then by definition, $\lim\limits_{x \to a} g(x) = g(a)$. This simplifies the substitution rule.
If $f$ is continuous at $y = g(a)$, then $$\lim_{x \to a} f(g(x)) = f(g(a)) \qquad (1)$$
Let us consider the composition: $$h(x) = f(g(x))$$
Rewrite (1) as $$\lim_{x\to a} h(x) = h(a) $$ Hence, $h$ is continuous at $x=a$ (by definition).
In other words...
Theorem. If $g$ is continuous at $x=a$ and if $f$ is continuous at $y=g(a)$, then $f \circ g$ is continuous at $x = a$.
Corollary. The composition of continuous functions is continuous.
Examples.
- $e^{x^{2}}$ is continuous.
- $e^{y}$ and $x^{2}$.
- $\sin x^{3}$ is continuous.
- $\sin y$ and $x^{3}$ is continuous.
Topology
Started to discuss continuity with:
- "the graph is a single piece" (informal)
then via limits:
- "the graph does not have a cut at point $a$".
That's continuity at a point.
Continuity on interval = Continuity at every point of the interval.
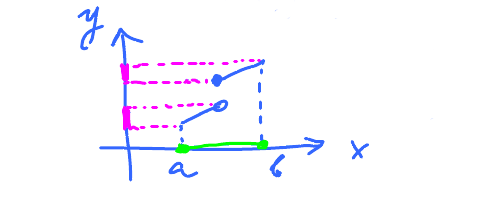
In other words, we have a "rope with no cuts". (Here $f$ is defined $[a,b]$ and continuous on $[a,b]$.) Is it the same as "one piece"? Yes. For the proof see Advanced calculus.
Informally, consider the "shadow" of the graph instead.
What about the $y$-axis? (range)
Is it one piece on the $y$-axis? I.e. is it a single interval?
Yes, if $f$ is continuous.
So, the projection of the graph of a continuous function on the $y$-axis is an interval.
Review exercise. Use the definition $\epsilon + \delta$ to prove $$\lim_{x\to 2} \left(\frac{1}{2}x + 2\right) = 3. $$ Choose $\delta=\frac{\epsilon}{2}.$
A more precise formulation of the above...
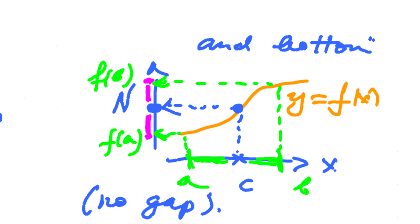
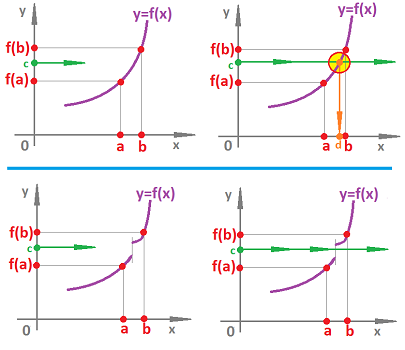
Intermediate Value Theorem. Suppose $f$ is continuous on $[a,b]$, then for every value of $N$ between $f(a)$ and $f(b)$ there is $c$ between $a$ and $b$ such that $$f(c) = N$$
or, to compare continuous and discontinuous:
The theorem can be restated:
Corollary. The range of a continuous function (defined on an interval) is an interval.
Review exercise. $$ y = \ln(\tan^{2} x) $$ it is continuous as it is the composition of three continuous functions. $$ x \to \underbrace{y = \tan x}_{x \neq \frac{\pi}{2} + kx,\quad k \text{ integer}} \to \underbrace{z = y^{2}}_{\text{all } y\text{'s}} \to \underbrace{u = \ln x}_{\text{all }z > 0}$$ All three are continuous on their domains.
We take the domain of the first function as a restriction to the domain of the function. The second has no effect. Finally, the third gives no restriction on the values of $z$. We need to find corresponding $x$'s.
So, solve $\tan^{2} x >0$. Observe that $\tan^{2} x \geq 0$
So, exclude $x$ such that $\tan x = 0$. Solve this equation, rewrite as $\frac{\sin x}{\cos x} = 0$, or $\sin x = 0$, hence $x \neq k\pi$, $k$ integer.
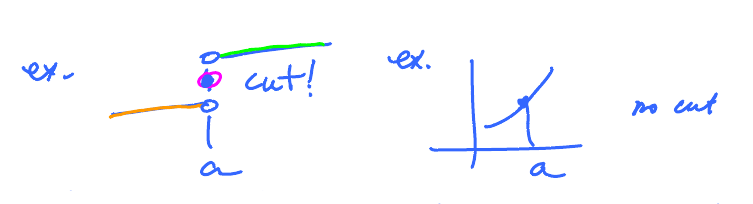






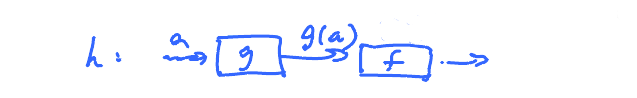

![Projection on the $x$-axis is $[a,b]$ (Domain).](/images/d/d4/GraphShadow.png)