Constant homotopy between constant maps

Learn how to fish...

Problem. Suppose $f_0,f_1:X\rightarrow Y$ are two constant maps. If they are homotopic, does this mean that there is a "constant" homotopy, i.e., the one with every function $f_t$ constant, between them? What does this have to do with path-connectedness?

Solution.

The short version of the solution, if you know it, fits in this little box: $$[...........]$$

However, what if we don't see the solution yet?

Let's first re-write the problem in a more concrete way:

• given $f_0,f_1:X\rightarrow Y$, that satisfy
• $f_0(x)=c\in Y, f_1(x)=d\in Y$ for all $x\in X$;
• also given a homotopy $f_0\sim^F f_1$, where $F:[0,1]\times X\rightarrow Y$, with $F(t,\cdot)=f_t$.

Is there a homotopy $f_0\sim^G f_1$, where $G:[0,1]\times X\rightarrow Y$, with $G(0,\cdot)=f_0,G(1,\cdot)=f_1$ and $G(t,x)=g(t)$ for all $t,x$?

Next, we will attempt to "trivialize" the set-up until the solution becomes obvious, but not too obvious.

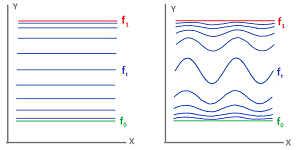
The simplest set-up would appear to be a map from interval to interval. Below we show a constant, $G$, and a non-constant, $F$, homotopies between two constant maps:

Of course, this is too narrow as any two maps are homotopic under these circumstances: $Y$ is convex. The target space is too simple!

To get around this problem we should

• try to imagine that $Y$ is slightly bent, and then
• try to build $G$ directly from $F$.

Sounds like a plan but, really, how do we straighten out these waves?

The fact that this question seems too challenging indicates that the domain space is too complex!

But what is the simplest domain? A single point!

In this case all homotopies are constant. The domain space is too simple!

What is the next simplest domain? Two points!

Let's make the set-up more concrete:

1. Given $f_0,f_1:\{a,b\}\rightarrow [c,d]$ (bent),
2. $f_0(a)=f_0(b)=c, f_1(a)=f_1(b)=d$;
3. also given a homotopy $f_0\sim^F f_1$, where $F:[0,1]\times \{a,b\}\rightarrow [c,d]$, with $F(t,\cdot)=f_t$.
4. Find a homotopy $f_0\sim^G f_1$, where $G:[0,1]\times \{a,b\}\rightarrow [c,d]$, with $G(0,\cdot)=f_0,G(1,\cdot)=f_1$ and $G(t,a)=G(t,b)$ for all $t$.

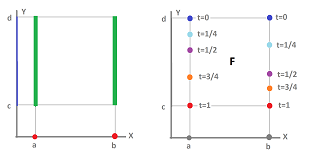
The set-up is as simple as possible. As the picture on the left shows, everything is happening within these two green segments.

Meanwhile the picture on the right shows that the homotopy $F$ can be non-trivial: $d$ is "moved" to $c$ but at two different paces.

The set-up is now very simple but the solution isn't obvious yet. That's what we want for our analysis!

Items 1 and 2 tell us that there are just two values, $c$ and $d$, here. Item 3 indicates that there are just two functions, $F(\cdot,a)$ and $F(\cdot,b)$ here, and item 4 asks for just one function, $G(\cdot,a)$ same as $G(\cdot,b)$.

How do we get one function from two?!

It is tempting to try to combine them algebraically (via a convex combination or similar) but remember $[c,d]$ is bent and no algebra is allowed.

So, we need to construct $G(\cdot,a)=G(\cdot,b)$ from $F(\cdot,a)$ and $F(\cdot,b)$.

What to do?..

Fill the box: $$[...........]$$