College Algebra -- Fall 2016 -- midterm

Name:_________________________ $\qquad$ 8 problems, 80 points total

• Show enough work to justify your answers.
• Write the problems in the given order, each problem on a separate page.

$\bullet$ 1. Factor: $3x^2-6x+3$.

$\bullet$ 2. Find the equation of the line passing through the points $(-1,1)$ and $(-1,5)$.

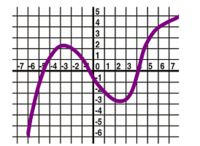
$\bullet$ 3. The graph of a function $f(x)$ is given below. (a) Find $f(-4)$, $f(0)$, and $f(4)$. (b) Find such an $x$ that $f(x)=2$. (c) Is the function one-to-one?

$\bullet$ 4. Find the inverse of the function $f(x)= 3x^2+1$. Choose appropriate domains for these two functions.

$\bullet$ 5. Restate (but do not solve) the following problem algebraically: “What are the dimensions of the rectangle with the smallest possible perimeter and area fixed at $100$?”

$\bullet$ 6. (a) Solve the equation $(x^2+1)(x+1)(x-1)=0$. (b) Solve the inequality $(x^2+1)(x+1)(x-1)>0$.

$\bullet$ 7. Find the composition $h(x)=(g\circ f)(x)$ of the functions $y=f(x)=x^{2}-1$ and $g(y)=\frac{y-1}{y+1}.$ Evaluate $h(0)$.

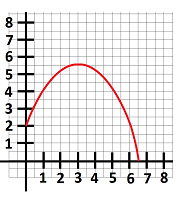
$\bullet$ 8. The graph of the function $y=f(x)$ is given below. Sketch the graph of $y=2f(x)$ and then $y=2f(x)-1$.