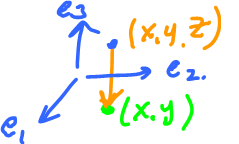Linear operators: part 5

Rank and nullity of a linear operator

Based on the discussion above:

Theorem: Given a linear operator $A \colon V \rightarrow U$ and its matrix (for some basis), the image ${\rm im \hspace{3pt}}A$ is spanned by the column vectors of the matrix (called the column space).

Given a linear operator $A \colon V \rightarrow U$, define the rank of $A$ as the dimension of the image of $A$: $${\rm rank \hspace{3pt} A} = {\rm dim \hspace{3pt} im \hspace{3pt}}A.$$

Then the theorem above tells us that

• ${\rm rank \hspace{3pt}}A \leq $ number of columns in $A$, and even
• ${\rm rank \hspace{3pt}}A = $ number of linear independent columns in $A$,

that's the rank of the matrix. (equal to the number of linearly independent rows, exercise)

Define the nullity of $A$ is the dimension of the kernel of $A$: $${\rm nul \hspace{3pt}} A = {\rm dim \hspace{3pt} ker \hspace{3pt}}A.$$

It tells how much not one-to-one $A$ is.

What is the relation between rank and nullity?

Example: Look at the projection (always the best example): $$P \colon {\bf R}^3 \rightarrow {\bf R}^2, (x,y,z) \rightarrow (x,y).$$

Find: rank=? nul=?

$${\rm rank \hspace{3pt}}P = {\rm dim \hspace{3pt} im \hspace{3pt}}P = {\rm dim \hspace{3pt}} {\bf R}^2 = 2.$$

$${\rm nul \hspace{3pt}}P = {\rm dim \hspace{3pt} ker \hspace{3pt}}P = {\rm dim \hspace{3pt}}z{\rm -axis \hspace{3pt}}=1.$$

Example: Projection $P \colon {\bf R}^3 \rightarrow {\bf R}^2.$

$${\rm rank \hspace{3pt}}P = {\rm dim \hspace{3pt}} {\bf R}^2 = 1.$$

$${\rm nul \hspace{3pt}}P = {\rm dim \hspace{3pt}}y{\rm -axis \hspace{3pt}}=1.$$

Example: General projection $P \colon {\bf R}^n \rightarrow {\bf R}^m$, $m \leq n$, given $$P(x_1,\ldots,x_n) = (x_1,\ldots,x_m).$$ Then

• $P$ is onto, so ${\rm rank \hspace{3pt}} P = m$.
• $P$ is not one-to-one. Find ${\rm ker \hspace{3pt}} P$.

$$\begin{array}{} {\rm ker \hspace{3pt}}P &= \{(x_1,\ldots,x_n) \colon P(x_1,\ldots,x_n)=0 \} \\ &= \{ (x_1,\ldots,x_n) \colon (x_1,\ldots,x_m) = 0 \} \\ &= \{ (0,\ldots,0, x_{m+1},\ldots,x_n) \colon x_{m+1},\ldots,x_n \in {\bf R} \} \end{array}$$

$$\begin{array}{} {\rm nul \hspace{3pt}}P &= {\rm dim \hspace{3pt} ker \hspace{3pt}} P \\ &= {\rm dim \hspace{3pt}} {\bf R}^{n-m} \\ &= n-m. \end{array}$$

Observe that rank and nullity match: $(m)+(n-m)=n$. Suggests that this is a rule.

Theorem: Given a linear operator $A \colon V \rightarrow U$ with $V$ finite dimensional space, then

$${\rm rank \hspace{3pt}}A + {\rm nul \hspace{3pt}}A = {\rm dim \hspace{3pt}} V$$

(splits!)

To prove this, we need to study the structure of these spaces as related to the operator...

What happens to the basis of $V$ under $A$?

The idea is based on this simple example:

$$\{e_1,e_2,e_3 \} \stackrel{A}{\rightarrow} \{e_1,e_2\},$$

basis of the image (it will give us the rank).

What about $e_3$? $e_3 \stackrel{A}{\rightarrow} 0$.

Then $\{e_3\}$ forms a basis of ${\rm ker \hspace{3pt}} A$.

Here operator matches the standard basis...

In general, start with a basis of ${\rm ker \hspace{3pt}}A$ (key step), $\{v_1,\ldots,v_m\}$.

Where does a basis of ${\rm im \hspace{3pt}}A$ come from?

To find it, complete $\{v_1,\ldots,v_m\}$ to a basis (key step) of the whole $V$: $\{v_1,\ldots,v_m,\ldots,v_n\}$.

Why is it possible? Expansion Theorem.

Linear operator and generated subspaces

We are given a linear operator $A \colon V \rightarrow U$ with $V$ finite dimensional.

Plan: The basis we choose for $A$ is what's left after we took out the basis of ${\rm ker \hspace{3pt}}A$:

$$\begin{array}{} {\rm space} & {\rm basis} \\ V & \{v_1,\ldots,v_m,\ldots,v_n\} \\ {\rm ker \hspace{3pt}}A & \{v_1,\ldots,v_m\} \\ {\rm left} & \ldots \ldots \{v_{m+1},\ldots,v_n\}. \end{array}$$

Note: these are in $V$ but ${\rm im \hspace{3pt}}A \subset U$.

Consider $$D = \{A(v_{m+1}),\ldots,A(v_n)\}$$ ($(n-m)$ of them).

Prove that it is a basis of ${\rm im \hspace{3pt}}A$.

Part (A).

Prove that ${\rm span \hspace{3pt}}D={\rm im \hspace{3pt}}A$.

Take $u \in {\rm im \hspace{3pt}}A$ and show that $u$ is a linear combination of $D$. How?

$$u \in {\rm im \hspace{3pt}}A \Rightarrow u = A(v).$$ gor some $v \in V$.

Then $$v=a_1v_1+\ldots+a_nv_n$, $a_1,\ldots,a_n \in {\bf R}$$ (remember $\{v_1,\ldots,v_n\}$ is a basis of $V$).

Apply $A$ (use linearity): $$\begin{array}{} u &= A(v) \\ &= A(a_1v_1+\ldots+a_nv_n) \\ &= a_1A(v_1) + \ldots + a_nA(v_n) \end{array}$$ ($n$ elements here).

This is a linear combination but not the same as $D$ ($(n-1)$ elements).

$$=a_1A(v_1)+\ldots+a_mA(v_m)+a_{m+1}A(v_{m+1}+\ldots+a_nA(v_m)$$

Here the terms up through the $m^{\rm th}$ are not in $D$ (they are known), the ones after are a linear combination of elements of $D$.

These are a basis $(v_1,\ldots,v_m)$ of ${\rm ker \hspace{3pt}}A$, so...

$$=0 + \ldots + 0 + a_{m+1}A(v_{m+1}) + \ldots + a_nA(v_n).$$

So, $u$ is a linear combination of elements of $D$, Hence $D$ spans ${\rm im \hspace{3pt}}A$.

Part (B).

Prove that $D$ is linearly independent.

Same idea:

• 1. Set it up in ${\bf M}$,
• 2. Then take back to $V$,
• 3. Use basis, then
• 4. Bring it back to $U$.

Suppose

$$\lambda_{m+1}A(v_{m+1})+\ldots+\lambda_nA(v_n) = 0$$

for some $\lambda_{m+1},\ldots,\lambda_n \in {\bf R}$ (here $A(v_i)$ are elements of $D$).

To get $A$ alone, use linearity, rewrite:

$$A(\lambda_{m+1}v_{m+1}+\ldots+\lambda_nv_n) = 0$$

Input to $A$ is in $V$, in fact this element:

• 1. $v=\lambda_{m+1}v_{m+1}+\ldots+\lambda_nv_n$.

It satisfies $A(v)=0$, so $v \in {\rm ker \hspace{3pt}}A$. Hence, use its basis $\{v_1,\ldots,v_m\}$. So,

• 2. $v = \lambda_1v_1+\ldots+\lambda_mv_m$,

for some $\lambda_1,\ldots,\lambda_m \in {\bf R}$.

Now $v$ is written in two ways 1 and 2.

$$(*) v=\lambda_1v_1+\ldots+\lambda_mv_m= \lambda_{m+1}v_{m+1}+\ldots+\lambda_nv_n.$$

So what? Let's compare left hand side to right hand sides.

Sidenote: Alternatively, $$\lambda_1v_1+\ldots+\lambda_mv_m - \lambda_{m+1}v_{m+1} - \ldots - \lambda_nv_n = 0$$

is a linear combination of $\{v_1,\ldots,v_n\}$, basis of $V$, so all the coefficients are $0$'s.

On the one hand:

• $\{v_1,\ldots,v_m\}$ basis of ${\rm ker \hspace{3pt}}A$.

On the other hand:

• $\{v_{m+1},\ldots,v_n\}$ was added to complete a basis of $V$ (the proof of the Expansion Theorem).

Then, recall

• $v_{m+1} \not\in {\rm span \hspace{3pt}} \{v_1,\ldots,v_m\}$
• ...
• $v_n \not\in {\rm span \hspace{3pt}} \{v_1,\ldots,v_{n-1}\}$

So, at least, $$v_{m+1},\ldots,v_n \not\in {\rm span \hspace{3pt}} \{v_1,\ldots,v_m\} = {\rm ker \hspace{3pt}}A.$$

So what? What does (*) tell us?

The only vector they have in common is $0$, so $$\lambda_1=\ldots=\lambda_m=\ldots=\lambda_n=0.$$

So, go back to $U$, observe that $A(v_{m+1}),\ldots,A(v_n)$ are linearly independent. $\blacksquare$

One can extract from the proof information about the structure of $V,U, {\rm ker \hspace{3pt}}A, {\rm im \hspace{3pt}}A,$ beyond their dimensions (exercise):

$${\rm dim \hspace{3pt} ker \hspace{3pt}}A + {\rm dim \hspace{3pt} im \hspace{3pt}}A = {\rm dim \hspace{3pt}}V$$

That's our theorem.

Corollary: $A$ is one-to-one if and only if ${\rm ker \hspace{3pt}}A = \{0\}$.

Proof:

$$\Longleftrightarrow {\rm dim \hspace{3pt} ker \hspace{3pt}}A = 0 \Longleftrightarrow {\rm dim \hspace{3pt} im \hspace{3pt}}A = {\rm dim \hspace{3pt}}V \Longleftrightarrow {\rm im \hspace{3pt}}A=V$$

Theorem: Suppose $A \colon V \rightarrow U$ linear.

• 1. If $A$ is one-to-one and $\{v_1,\ldots,v_n\}$ linearly independent, then $\{A(v_1),\ldots,A(v_n)\}$ is linearly independent.
• 2. If $A$ is onto and $\{v_1,\ldots,v_n\}$ spans $V$, then $\{A(v_1),\ldots,A(v_n)\}$ spans $U$.

That's an exercise.

Classification theorem of vector spaces

Theorem. Suppose $U,V$ are finite dimensional vector spaces. Then $U$ and $V$ are isomorphic if and only if $${\rm dim \hspace{3pt}}U = {\rm dim \hspace{3pt}} V.$$

Example: ${\bf R}^4$, ${\bf P}^3$, ${\bf M}(2,2)$: dimension=$4$.

Lesson: Only coefficients matter for algebra!

Proof: Construct an isomorphism: linear, one-to-one, onto, $A \colon U \rightarrow V$.

• ${\rm dim \hspace{3pt}}U=n$ implies there is a basis $\{u_1,\ldots,u_n\}$
• ${\rm dim \hspace{3pt}}V=n$ implies there is a basis $\{v_1,\ldots,v_n\}$.

So what do we do?

We match the elements of the bases. We define $$A(u_i)=v_i$, $i=1,\ldots,n.$$

We know that it suffices to define a linear operator on the basis only. This part is done.

Prove that $A$ is one-to-one. Look at

$$\begin{array}{} {\rm ker \hspace{3pt}}A &= \{u \colon A(u) = 0 \} \\ &= \{u \colon A(a_1u_1+\ldots+a_nu_n)=0 \} \\ &= \{u \colon a_1A(u_1) + \ldots + a_nA(u_n) = 0 \} \\ &= \{ u = a_1u_1 + \ldots + a_nu_n \colon a_1v_1 + \ldots + a_nv_n = 0 \} \\ &= \{u = 0a_1 + \ldots + 0a_n \} \\ &= \{0\}, \end{array}$$ Here $v_i$ are basis elements, they are linearly independent, so $a_1=\ldots=a_n=0$.

So by theorem, $A$ is one-to-one.

Similarly, to prove that $A$ is onto, look at $${\rm im \hspace{3pt}}A = \{v \in V \colon v =A(u) {\rm \hspace{3pt} for \hspace{3pt} some \hspace{3pt}} u \in U \}.$$

Take $v \in V$, show that $v \in {\rm im \hspace{3pt}}A$. How?

Represent $$\begin{array}{} v &= b_1v_1+\ldots+b_nv_n \\ &= b_1A(u_1) + \ldots + b_nA(u_n) \\ &= A(b_1u_1 + \ldots + b_nu_n) \\ &= A(w), \end{array}$$

where $u=b_1u_1 + \ldots + b_nu_n$, so $v \in {\rm im \hspace{3pt}}A$ and $A$ is onto. $\blacksquare$

This is really important...

Theorem: Isomorphism is an equivalence relation on the set of all vector spaces.

Proof: Check the axioms: (2) $V \sim U \rightarrow U \sim U$ (symmetry).

Indeed, suppose $A \colon V \rightarrow U$ is an isomorphism, then we need $B \colon U \rightarrow V$ also an isomorphism.

Choose $B=A^{-1}$, it exists because $A$ is one-to-one, onto, and linear by theorem.

• 1. (Reflexivity) $V \sim V$, why? Need $A \colon V \rightarrow V$ an isomorphism, choose $A = {\rm id}_V$.
• 3. (Transitivity) $V \sim U$, $U \sim W$, the $V \sim W$.

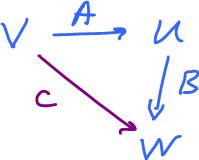
$$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} V & \ra{A} & U \\ C \searrow & & \da{B} \\ & & W \end{array} $$

Given $A,B$ two isomorphisms. Complete the diagram with the composition $C = BA$. Easy to prove that $C$ is an isomorphism. \blacksquare$

Partition of all finite-dimensional vector spaces:

Best representations: ${\bf R}^0$-${\bf R}^1$-${\bf R}^2$-${\bf R}^3$-${\bf R}^4$-

It's similar to modular arithmetic: ${\bf Z}$ $a \sim b$ if $a = b {\rm \hspace{3pt} mod \hspace{3pt}}n$ same remainder after division by $n$.

$n=3$

Partition of ${\bf Z}$ into three classes. Create $${\bf Z}_3 = \{0,1,2\}$$ with algebra. Each is the best representation of each class.