Rates of change

We will consider a new examples of applications of the derivative as the rate of change of a variable. However, let's recall the example -- where calculus came from.

The Example

$x$ is time, $y(x)$ is the position.

• Horizontal motion:

Motion along straight line

$\frac{dy}{dx}=f^{\prime}(x)$ is the velocity.

• Vertical motion (altitude):

• Typically, know the position (from odometer), find velocity.
• Also, know the velocity (from speedometer), find the position.

Example. $f^{\prime}(x) = 2x$, what is $f$? $$\begin{aligned} f(x) &= x^{2} \\ f(x) &= x^{2} + C. \end{aligned}$$ This is called anti-differentiation.

Other Examples:

• Exponential growth/decay: Different but $x$ is still time (below).

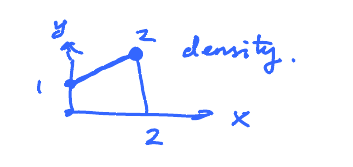
Linear Density

Given a metal rod.

Uniform Pure Metal Bar

Define: $\text{linear density} = \frac{\text{mass}}{\text{length}}$.

Technically, this is the average density. What if the rod isn't uniform, like an alloy? For example, suppose we have two pieces of different metals, the we melt them together (no stir!).

Non-Uniform Metal Bar

Suppose the densities are 1 lbs/in and 2 lbs/in at the ends respectively. Then the density of this alloy will gradually change from 1 to 2.

This is the "mass function" of $x$, the location: $y=m(x)$ is the mass of the rod from $O$ to $x$. Consider how $m$ is changing:

Mass function with respect to $x$.

Take a small piece of the rod, $\Delta x$ long. Then $$ \text{Average Density} = \frac{\text{Mass}}{\text{Length}} = \frac{\Delta m}{\Delta x} = \frac{m(x + \Delta x) - m(x)}{\Delta x}$$ So, $$ \text{linear density} = \lim_{\Delta x \to 0} \frac{\Delta m}{\Delta x} = m^{\prime}(x) $$

Bar of Non-Uniform Density 1 lbs/in & 2 lbs/in. What is the total mass?

Density Distribution of Bar

$$ \text{Mass} = \text{Average Density} \cdot \text{Length} = 1.5 \cdot 2 = 3 $$

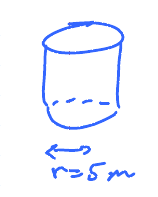
Rising water in a cylinder tank

This is a word problem about related rates.

Given a cylindrical water tank:

1. Radius 5
2. Water is pumped in at $3 \frac{\text{m}^{3}}{\text{min}}$,
3. How fast is the level increasing?

Solution.

I. First name things, all of them:

• $r$ radius,
• $V$ volume,
• $A$ Area of the bottom,
• $H$ Height of water,
• $t$ time.

II. Collect information about by rephrasing the data in the problem in terms of these variables:

1. $r=5$
2. $\frac{dV}{dt}=3$
3. $\frac{dH}{dt} = ?$

III. Connect these variables (using the geometry of the situation):

$$\left.\begin{aligned} A & = \pi r^{2} \\ V &= AH \end{aligned} \right\} \to V = \pi r^{2} H = 25\pi H $$

IV. Differentiate the equation in (III).

$$\begin{aligned} \frac{d}{dt}\left(V\right) &= \frac{d}{dt}\left( 25 \pi H\right) \\ \frac{dV}{dt} & = 25 \pi \frac{dH}{dt} \end{aligned} $$

V. Substitute data we know. $$\begin{aligned} 3 &= 25 \pi \frac{dH}{dt} \\ \text{So } \frac{dH}{dt} &= \frac{3}{25\pi} \frac{\text{m}}{\text{min}}\end{aligned}$$

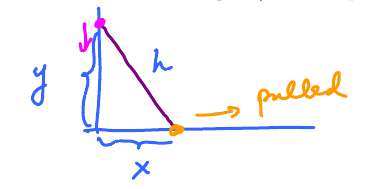
Ladder leaned against a wall

A ladder stands against the wall:

1. 10 ft. ladder
2. Bottom moves 1 ft/sec.
3. Question: How fast is the top moving when the bottom is 6 ft from the wall?

Diagram of falling ladder leaning against wall.

Introduce variables $x$, $y(h)$, functions of time, $t$. Translate the variables into equations. Translate the geometry too.

1. $h = 10$
2. $\frac{dx}{dt} = 1$
3. $\frac{dy}{dt} = ?$ when $x = 6$.
4. $x^{2} + y^{2} = h^{2}$

This is all we need. (No need for the words or the picture anymore.)

Simplify:
Given: $$\begin{aligned} x^{2} + y^{2} & = 100, \\ \frac{dx}{dt} &= 1 \end{aligned}$$ Find $\frac{dy}{dt}$ for $x=6$.

Differentiate the equation with respect to the independent variable: $$\begin{aligned} \frac{d}{dt}\left( x^{2} + y^{2} \right) & = \frac{d}{dt}\left(100\right) \\ 2x\frac{dx}{dt} + 2y\frac{dy}{dt} & = 0, \text{ solve for } \frac{dy}{dt} \\ \frac{dy}{dt} &= - \frac{x}{y}\frac{dx}{dt}, \text{ substitute } \\ &= -\frac{6}{y} 1, \\ & \text{ Now } y \text{ comes from } x^{2} + y^{2} = 100 \\ &= -\frac{6}{8} \\ & = -\frac{3}{4} \end{aligned} $$