Calculus I -- Fall 2018 -- midterm

MATH 229 -- Fall 2018 -- Midterm exam

Name:_________________________ $\qquad$ 8 problems, 10 points each

• Write the problems in the given order, each problem on a separate page.
• Show enough work to justify your answers; make reference to theorems and definitions.

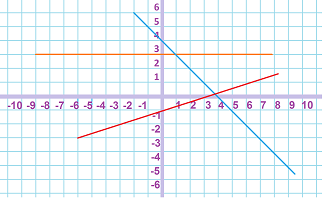
$\bullet$ 1. Three straight lines are shown below. Find their slopes:

$\bullet$ 2. Your location is recorded every half-hour, shown below. Estimate your velocity as a function of time. $$\begin{array}{r|c} \text{time, }x&\text{location, }y\\ \hline 0&20\\ .5&30\\ 1&20\\ 1.5&20\\ 2&50\\ \end{array}$$

$\bullet$ 3. Sketch, when possible, the graph of (a) a function that is continuous but not differentiable, (b) a function that is differentiable but not continuous, (c) a function with $f'(c)=0$ but no extreme point at $c$.

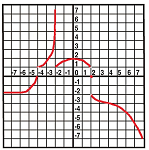
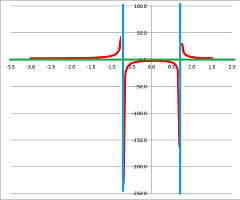
$\bullet$ 4. Using one-sided limits, describe the behavior of the two functions sketched below:

$\bullet$ 5. From the definition (look it up!), compute the derivative of $f(x)=-x^2+x$ at $x=1$.

$\bullet$ 6. Sketch the graph of the derivative of the second function given in problem #4. Identify all important features of the graph.

$\bullet$ 7. Find the derivative of the function $f(x)=\cos \sqrt{x}$.

$\bullet$ 8. Find the derivative of the function $f(x)=e^{\sin x}$.