Calculus II -- Spring 2018 -- midterm

MATH 230 -- Spring 2018 -- midterm exam

Name:_________________________ $\qquad$ 7 problems, 10 points each

• Write the problems in the given order, each problem on a separate page.
• Show enough work to justify your answers.

$\bullet$ 1. Evaluate the integral by substitution $$\int xe^{x^{2}}\, dx.$$

$\bullet$ 2. Evaluate the improper integral: $$\int_1^{\infty} \frac{1}{2x}\, dx.$$

$\bullet$ 3. Execute the following substitution in the integral (don't evaluate the resulting integral): $$\int \sqrt{1+\sin x}\, dx,\quad u=\sin x.$$

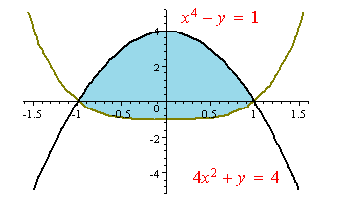
$\bullet$ 4. Find the area enclosed by the curves below:

$\bullet$ 5. Find the center of mass of the region bounded by the curves $y=4-x^{2},\ y=-2$.

$\bullet$ 6. Evaluate the limit if it exists: $\lim_{n\to \infty}\ln \left({\frac{n}{n+1}} \right).$

$\bullet$ 7. Give an example of a sequence for each of the following: (a) $a_n\to 0$ as $n\to \infty$, (b) $a_n\to 1$ as $n\to \infty$, (c) $a_n\to +\infty$ as $n\to \infty$, (d) $\{a_n\}$ diverges but not to infinity.