Calculus II -- Fall 2018 -- midterm

MATH 230 -- Fall 2018 -- Midterm exam

Name:_________________________ $\qquad$ 8 problems, 10 points each

• Write the problems in the given order, each problem on a separate page.
• Show enough work to justify your answers.

$\bullet$ 1. Execute the substitution $u=e^x$ for the integral (don't evaluate the resulting integral): $$\int \sin (1+e^x)\, dx.$$

$\bullet$ 2. Find the area enclosed by the curves $y=x^2$, $y=-x^3$, and the line $x=1$.

$\bullet$ 3. Set up but do not evaluate the Riemann sums and the integral for the volume of a box $A\times B\times C$ in terms of its cross-sections.

$\bullet$ 4. Suppose a sequence is defined recursively by $$a_{n+1}=2a_n+1\text{ with } a_0=1.$$ Does the sequence converge or diverge?

$\bullet$ 5. Give formulas for the following sequences: (a) $a_n\to 0$ as $n\to \infty$ but it's not increasing or decreasing; (b) $b_n\to +\infty$ as $n\to \infty$ but it's not increasing.

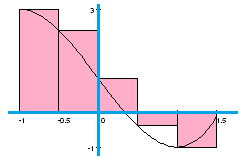
$\bullet$ 6. If the graph below represents the velocity of an object as a function of time, what does the shaded area (the Riemann sum) represent?

$\bullet$ 7. Evaluate the improper integral: $$\int_1^{\infty} e^{-2x}\, dx.$$

$\bullet$ 8. Apply the Integration by Parts formula to the integral, $$\int xe^x\, dx,$$ with these two choices of the “parts”:

• (a) $x$ and $e^x\, dx$,
• (b) $e^x$ and $x\, dx$.