This site is being phased out.
Calculus III -- Spring 2014 -- final exam
Name:_________________________
10 problems, 10 points each
- Justify every step you make with as thorough explanation as possible.
- Unless requested, no decimal representation of the answers is necessary.
- Start every problem at the top of the page.
$\bullet$ 1. (1) Sketch the parametric curve $x=\cos t,y=\sin 2t$. (2) The curve intersects itself. Find the angle of this intersection.
$\bullet$ 2. Sketch the graph of a function of two variables $z=f(x,y)$ the derivatives of which have the following signs: $f_x>0, f_{xx}>0, f_y<0, f_{yy}<0$.
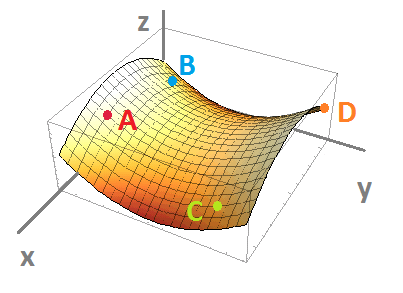
$\bullet$ 3. The graph of a function of two variables $z=f(x,y)$ is given below along with four points on the graph. Sketch the gradient for each on a separate $xy$-plane:
$\bullet$ 4. Give the definition of the curvature. Give examples of curves with various curvatures.
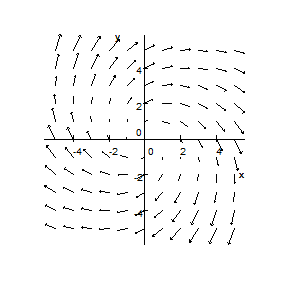
$\bullet$ 5. A vector field is sketched below. Suppose $C$ is the clockwise oriented square centered at the origin. Is $\int _{C}\mathbf{F}\cdot d\mathbf{r}$ positive, negative or $0$? Explain.
$\bullet$ 6. This is the formula of Green's Theorem: $$\oint_{C} (L\, dx + M\, dy) = \iint_{D} \left(\frac{\partial M}{\partial x} - \frac{\partial L}{\partial y}\right)\, dA. $$ Explain its parts and the conditions that have to be satisfied.
$\bullet$ 7. Prove that the vector field $F(x,y,z)=z\mathbf{j} - y\mathbf{k}$ is not conservative.
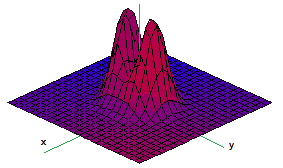
$\bullet$ 8. Make a sketch of contour (level) curves for the function below:
$\bullet$ 9. Sketch the vector field $$F(x,y)=\dfrac{1}{x^{2}+y^{2}}(y\mathbf{i}-x\mathbf{j}).$$
$\bullet$ 10. Find the work done by force field $$F(x,y)=< xy,y^{2}>.$$ in moving an object along the parabola $x=t,y=t^{2},0\leq t\leq1.$
$\bullet$ 11. Use a Riemann sum with $8$ terms to estimate the value of the integral $$\iiint_{D}(x+y+z)dV,$$ over the cube $D=[0,1]\times[0,1]\times[0,1]$. Choose your own sample points.
$\bullet$ 12. (1) Represent the cylinder of radius $1$ and height $1$ centered on the $z$-axis as a parametric surface. (2) Find the tangent plane to the cylinder at the point $(\sqrt{2}/2,\sqrt{2}/2,1/2)$. (3) Compute the flux of the vector field $F=< 2,1,1 >$ across the part of the cylinder that lies in the first octant.
$\bullet$ Extra credit problem. (5 points, no partial credit) Suppose you are towing a trailer-home. During the first few minutes, every time you look at the rear view mirror you can see only the lower part of the home. Later, every time you look you can see only the top part. Discuss the profile of the road.