Calculus 2: final

Grading

This is a final exam for Calculus 2: course.

1. Set up the Riemann sum and the integral for the Disk Method for computation of the volume of the right circular cone whose radius of the base is 1 and the height is 1.
2. Find by integration the length of a circle of radius r.
3. Evaluate the integral: $∫\ln x/x²\,dx$.
4. Evaluate the integral: $∫\cos t/(\sin ²t(\sin t+1))dt$.
5. Test the following series for convergence (including absolute/conditional): $∑\sin ²n/√(n⁵-1)$.
6. Find the radius and the interval of convergence of the series $∑(1+n)(x+2)ⁿ/2ⁿ$.
7. Find the Taylor polynomial of order 2 centered at a=1 of the function $f(x)=e^{x²}$.
8. Find an equation of the line tangent to the parametric curve $x=4\cos θ,y=3\sin θ$ at the point corresponding to $θ=3π/4$.
9. Find a polar representation of a spiral wrapping around a circle - from the inside!
10. Complete the following: (a) "The sum of a series $∑_{n=1}^{∞}$ is ..." (b) "The ellipse is the set of points ..."
11. Indicate which the following statements below is true or false (no proof necessary):
    1. If the series $∑_{n=1}^{∞}a_{n}$ and $∑_{n=1}^{∞}b_{n}$ diverge then the series $∑_{n=1}^{∞}(a_{n}+b_{n})$ also diverges.
    2. The series $1/7²+1/8²+1/9²+1/10²+…$ converges.
    3. If $a_{n}>b_{n}>0$ and$ ∑_{n=1}^{∞}a_{n}$ converges, then $∑_{n=1}^{∞}b_{n}$ also converges.
    4. $∑_{n=1}^{∞}(-1)²ⁿ⁺¹(1/n)$ converges.
    5. If the series $∑(-1)ⁿa_{n}$ with $a_{n}>0$ converges absolutely then the series $∑a_{n}$ converges absolutely.

---

1. Evaluate the integral $$\int \sin^{3}t\cos^{2}tdt.$$
2. Evaluate the integral: $$\int x^{3}\sqrt{9-x^{2}}dx.$$
3. Evaluate $$\int_{-1}^{1}\dfrac{1}{\sqrt{|x|}}dx.$$
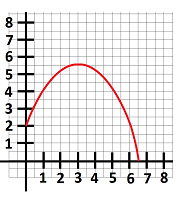
4. Let $I=\int_{0}^{6}f(x)dx.$ (a) Use the graph of $y=f(x)$ to estimate $L_{3},M_{3},R_{6}.$
   
   (b) Estimate $T_{3}$ and compare it to $I$.
5. The region bounded by the graphs of $y=\sqrt{x},y=0,$ and $x=1$ is revolved about the $x$-axis. Find the surface area of the solid generated.
6. Find (by integration) the length of a circle of radius $r.$
7. Find a parametric or polar representation of a curve similar to a spiral wrapping around a circle - from the inside! (no proof necessary).
8. (a) State the definition of the sum of a series. (b) Use (a) to show that the series $$\sum_{n=1}^{\infty}(\dfrac{1}{n+1}-\dfrac{1}{n})$$ converges.
9. Test the following series for convergence (including absolute/conditional): $$\sum\dfrac{\sin^{2}n}{\sqrt{n^{5}+1}}.$$
10. Find the radius and the interval of convergence of the series \[\sum_{n=1}^{\infty}\dfrac{(1+n)(x+2)^{n}}{2^{n}}.\]
11. Find the power series representation of the function $$f(x)=\dfrac{x^{2}% }{1-x^{2}}$$ and its interval of convergence.
12. Find the Taylor polynomial $T_{2}(x)$ of order $2$ centered at $a=\pi$ of the function $f(x)=\sin^{2}x.$
13. Indicate which the following statements below is true or false (no proof necessary):
    1. If the series $\sum_{n=1}^{\infty}a_{n}$ and $\sum_{n=1}^{\infty}b_{n}$ diverges then the series $\sum_{n=1}^{\infty}(a_{n}+b_{n})$ also diverges.
    2. The series $\frac{1}{7^{2}}+\frac{1}{8^{2}}+\frac{1}{9^{2}}+\frac{1}{10^{2}}+\ldots$ converges.
    3. If $a_{n}>b_{n}>0$ and $\sum_{n=1}^{\infty}a_{n}$ converges, then $\sum_{n=1}^{\infty}b_{n}$ also converges.
    4. The series $\sum_{n=1}^{\infty}(-1)^{2n+1}\dfrac{1}{n}$ converges.
    5. The sequence $\{1,\frac{1}{2},1,\frac{1}{3},1,\frac{1}{4},1,...\}$ converges to $0.$
14. Test for convergence: $$\sum(\sqrt[n]{2}-1).$$