This site is being phased out.
Area integral
Riemann integral defined over intervals can be generalized to functions of two variables integrated over rectangles and regions made of rectangles.
We consider
$$f: {\bf R}^2 \rightarrow {\bf R}.$$
The are of the rectangle
$$R = [ a, b ] \times [ c, d ]$$
is
$$A = (b - a)(d - c),$$
i.e. the area of the product of $2$ intervals is the product of their lengths.
In general, the area of each little rectangle is
The Riemann sum of $f: {\bf R} \rightarrow {\bf R}$ for this partition:
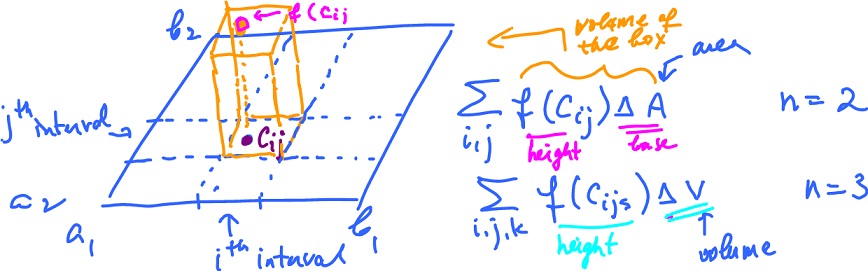
In dim = $2$:
Recall dim $= 1$. Consider
$$\displaystyle\lim_{k \rightarrow \infty} \displaystyle\sum_{i=1}^k f( c_i ) \Delta x$$
where $c_i$ denotes the midpoint of the respective intervals. If this limit exists, it is called the Riemann integral of $f$ from $a$ to $b$. We write
$$\displaystyle\int_a^b f(x) dx,$$
and call $f$ an integrable function on $[ a, b ]$.
For dim $= 2$ it's all very similar
$$\displaystyle\lim_{k \rightarrow \infty} \displaystyle\sum_{i=1}^k f( c_{ij} ) \Delta A = \displaystyle\int\displaystyle\int_R f(x) dA,$$
where
$$R = [ a, b ] \times [ c, d ].$$
Example. Let $f(x) = x, a = 0, b = 1$, and
Then
$$\begin{array}{} \displaystyle\lim_{k \rightarrow \infty} \displaystyle\sum_{i=1}^k f( c_i ) \Delta x \\ &= \displaystyle\lim_{k \rightarrow \infty} \displaystyle\sum_{i=1}^k c_i \Delta x \\ &= \displaystyle\lim_{k \rightarrow \infty} ( c_1 + ... + c_k ) \frac{1}{k} \\ &= \displaystyle\lim_{k \rightarrow \infty} ( 0 + (\frac{1}{k}) + (\frac{2}{k} ) + ... + (\frac{k-1}{k} ) k \\ &= \displaystyle\lim_{k \rightarrow \infty} ( (\frac{1}{k}^2) + (\frac{2}{k}^2) + ... + (\frac{k-1}{k}^2) ) {\rm \hspace{3pt} arithmetic \hspace{3pt} progression} \\ &= \frac{k \frac{k-1}{2}}{k^2} \\ &= \frac{1}{2} \end{array}$$
So,
$$\begin{array}{} \displaystyle\int_{[0,1]} x dx &= \displaystyle\int_0^1 x dx \\ &= \frac{x^2}{2}|_0^1 \\ &= \frac{1}{2}. \end{array}$$
Related: areas of regions in digital images.