Applied Calculus -- Spring 2015 -- midterm

Name:_________________________ $\qquad$ 8 problems, 10 points each

• Justify every step you make with as thorough an explanation as possible, in English.
• Unless requested, no decimal representation of the answers is necessary.
• Start every problem at the top of the page.

$\bullet$ 1. For the function $f(x)=\frac{2x^2}{7x^2-x+1}$, find its large scale behavior, i.e., $f(x)\to ?$ as $x\to \pm \infty$.

$\bullet$ 2. Represent this function $h(x)= \sqrt{x^2-1}$ as the composition of two functions. Find its derivative.

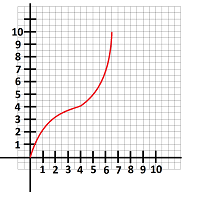
$\bullet$ 3. Describe the concavity of this function:

$\bullet$ 4. Sketch the graphs of functions with these features: (a) $f$ has a local maximum at $x=2$; (b) $g$ has a vertical asymptote at $x=1$; (c) $h$ has a horizontal asymptote at $y=-1$.

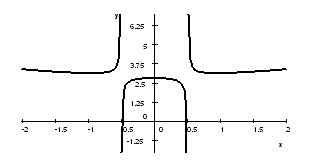
$\bullet$ 5. The graph of function $f$ is given below. List at least five of its main features.

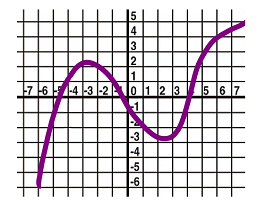
$\bullet$ 6. The graph of a function $f(x)$ is given below. Estimate the values of the derivative $f'(x)$ for $x=-4$, and $x=2.5$.

$\bullet$ 7. Calculate the derivative of $$f(x) = \frac{x^2}{x^2-1}.$$

$\bullet$ 8. Find all critical points of the function $f(x)=2x^3-6x+7$.