Applied Calculus -- Spring 2015 -- final exam

Name:_________________________ $\qquad$ 10 problems, 10 points each

• Justify every step you make with as thorough an explanation as possible, in English.
• Unless requested, no decimal representation of the answers is necessary.
• Start every problem at the top of the page.

$\bullet$ 1. Compute the derivative of $f(x)=e^{x^2+3x}$.

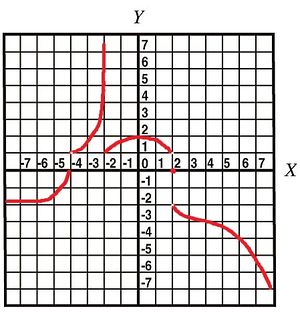
$\bullet$ 2. A sketch of the graph of a function $f$ is given below. List at least five of its main features.

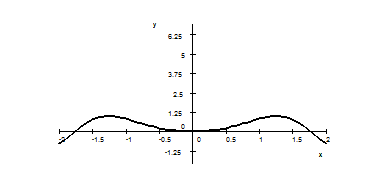
$\bullet$ 3. The graph of a function $f(x)$ is given below. Estimate the values of the derivative $f'(x)$ for $x=0$ and $x=4$. Show your computations.

$\bullet$ 4. Find the local maximum and minimum points of the function $f(x)=x^3-3x$.

$\bullet$ 5. Evaluate the integral $\int_0^1x^3dx$.

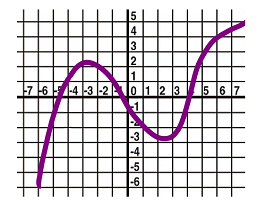
$\bullet$ 6. The graph of function $y=f(x)$ is given below. Sketch the graph of its derivative $y=f'(x)$.

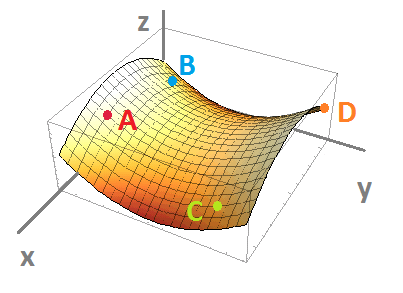
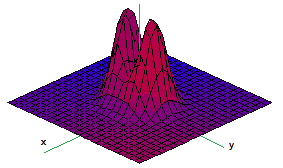
$\bullet$ 7. The graph of a function of two variables $z=f(x,y)$ is given below along with four points on the graph. Provide the signs (positive or negative) of the partial derivatives of $f$ at these points. For example, $\frac{\partial f}{\partial x}<0$ at point $A$.

$\bullet$ 8. Find all critical points of the function $f(x,y)=2x^3-6x+y^2-2y+7$.

$\bullet$ 9. Make a sketch of contour (level) curves for the following function:

$\bullet$ 10. The wave heights $h$ in the open sea depend on the speed $v$ of the wind and the length of time $t$ that the wind has been blowing at that speed. Values of the function $h=f(v,t)$ are recorded in the table below. Estimate the rate of change of $h$ with respect to $v$ when $v=40$ and $t=15$. Show your computations. $$\begin{array}{c|ccc} v\backslash t &15 &20 &25\\ \hline 30 &16 &17 &18\\ 40 &25 &28 &31\\ 50 &36 &40 &45 \end{array}$$