Algebra on graphs

Graphs

The very first data structure that needs to be analyzed topologically is graphs:

The examples of graphs shown come as networks of bridges, atoms in a molecule, related individuals, or computers.

Definition. A graph $G =(N,E)$ consists of two finite sets:

• the set of nodes $N=N_G$, and
• the set of edges $E=E_G$, which is a set of pairs of nodes. $\\$

We don't allow distinct edges for the same pair of nodes, nor doubles, such as $AA$, and we assume that $AB=BA$.

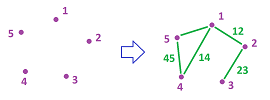
Example. Let's define a graph $G$ by:

• $N:=\{1,2,3,4,5 \}$, and
• $E:=\{12,23,45,14 \}$. $\\$

Let us be clear from the beginning that the dataset given above is the whole graph and what's below is just an illustration:

To draw an illustration, we first put the nodes in a more or less circular arrangement and then add the corresponding edges.

A common representation of a graph is via its incidence matrix, i.e., the matrix with a $1$ in the $(i,j)$-entry if the graph contains edge $ij$ and $0$s elsewhere. For $G$, we have: $$\begin{array}{c|cccccc} N & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 0 & 1 & 0 & 1 & 0 \\ 2 & 1 & 0 & 1 & 0 & 0 \\ 3 & 0 & 1 & 0 & 0 & 0 \\ 4 & 1 & 0 & 0 & 0 & 1 \\ 5 & 0 & 0 & 0 & 1 & 0 \end{array}$$ $\square$

Cycles

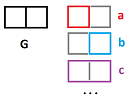
Definition. An edge-path in a graph $G$ from node $A$ to node $A$ is called a cycle (i.e., a $1$-cycle) in $G$.

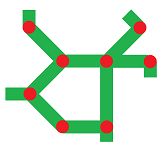
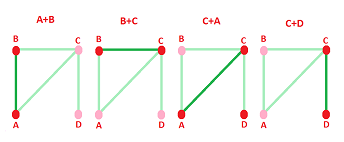
The graph $G$ below appears to have $2$ holes. However, the graph itself has (at least) $3$ cycles, $a,b,c$!

How do we eliminate the redundancy? We observe that combining $a$ and $b$ yields $c$:

File:TopologicalFigure8 and cycle algebra.png

Algebraically, it is: $$a+b=c.$$ In other words, the cycles are linearly dependent. That's why $c$ doesn't count.

Example. Let's consider our graph again:

Now consider our two cycles: $$\begin{array}{llllll} a & =12 + 25 + 56 + 61 \\ b & =23 + 34 + 45 + 52 \\ a+b & =12 + 25 + 56 + 61 + 23 + 34 + 45 + 52 \\ & =12 + (25 + 25) + 56 + 61 + 23 + 34 + 45 \\ & =12 + 56 + 61 + 23 + 34 + 45 \\ & = c \end{array}$$ Here we cancel the edge that appears twice. $\square$

Such cancelling is assured if we use the binary arithmetic: $$x+x=0,\ \forall x.$$ It is the arithmetic of integers modulo $2$, i.e., the algebra of ${\bf Z}_2$.

This idea takes us deep into algebra. One unexpected conclusion is that

$0$ is also a cycle!

Now, we list the four $1$-cycles that have no repeated edges: $$Z_1:=\{0 ,a,b,a+b\}.$$ It is a group.

Note: If we choose to stay within the realm of linear algebra, we have two options: either think of $Z_1$ as a vector space with coefficients over ${\bf Z}_2$ or enlarge $Z_1$ by including all of its real-valued linear combinations: $ra+sb,\ \forall r,s \in {\bf R}$. Then $\{a,b \}$ is a basis of this vector space and the idea becomes: $$\# \text{ of holes }= \dim Z_1 .$$ However, in order to assure cancellation, we would have to deal with the complexity of directed edges, with $AB \ne BA$. We will postpone following this idea until later.

Above, we have justified the use of binary arithmetic for edges but it is just as appropriate for the algebra of nodes. It suffices to consider the boundaries of edge-paths. Clearly, the boundary of an edge-path is the sum of its end-nodes. For instance, the path $12+23$ in the above graph has boundary $1+3$.

On the other hand, its boundary is the sum of the boundaries of $12$ and $23$. Those are $1+2$ and $2+3$. We end up with $$1+3 = (1+2) + (2+3).$$ Hence, $2+2=0$. That's binary arithmetic again.

The algebra of plumbing

We have been looking at the subsets of the sets of nodes and edges to study the topology of the graph. Next, we will pursue this analysis via a certain kind of algebra. We introduce this algebra with the following metaphor:

• One can think of a graph as a plumbing system that consists of a network of pipes and joints. There is no water yet.

Let's assume that each joint is equipped with an on-off switch.

Suppose the plumbers are, when necessary, told to “flip the switch”. Then two consecutive flips cause the switch to return to its original position. Furthermore, a sequence of such commands will result in another simple command: either “flip the switch” again or “do nothing”. Naturally, these two commands are represented as $1$ and $0$ and combining these commands is represented by the binary arithmetic of ${\bf Z}_2$: $$0+0=0,\ 1+0=1,\ 0+1=1,\ 1+1=0.$$

Now, this activity is happening at every joint. The plumber -- call him the joints guy -- receives complaints from the tenants about a possible leak in a given joint and a request to flip its switch.

Then a combined request is to flip a selection of switches, such as:

• flip switches at joints $A, B, ...$. $\\$

The joints listed appear in the requests several times or never. Requests may be issued at any time and combined with the outstanding ones. The plumber may, using binary arithmetic, reduce his workload one joint at a time. Or, he can combine two or more work requests into one as follows. The joints are ordered and these requests are recorded in a vector format, coordinate-wise. For instance, $(1,0,1,0, . . .)$ means: flip the first and third switches, etc. Then, $$(1,0,1,0, . . .)+(1,1,1,0, . . .)=(0,1,1,0, . . .).$$ Here, $0$ is the “do nothing” request. In other words, the algebra is that of this group: $$\Big( {\bf Z}_2 \Big)^n=\underbrace{{\bf Z}_2\oplus{\bf Z}_2\oplus ... \oplus {\bf Z}_2}_\text{n times},$$ where $n$ is the number of the joints in the network.

Let' also suppose that each pipe has, too, an on-off switch. There is also another plumber -- call him the pipes guy -- who flips these switches by request from the tenants. A combined request is to take care of a selection of pipes, such as:

• flip switches of pipes $a,b, ...$.

Once again, the pipes listed may appear several times and the requests may be issued at any time and combined with the outstanding one, using binary arithmetic. The set of all requests form a group: $\big( {\bf Z}_2 \big)^m,$ where $m$ is the number of the pipes in the network.

Now, there is no overlap between the activities of the two plumbers so far, and there is no relation between any two joints, or any two pipes, or a joint and a pipe. However, what if the pipes guy doesn't show up for work? Then one may try to amend his request, such as

• flip the switch of pipe $a$, $\\$

with a request for the joints guy. The choice of a substitution is obvious, if imperfect:

• flip the switches at ends of pipe $a$.

The result is a function, from the pipe requests to the joint requests: $$a=AB \ \mapsto \ A+B.$$ This is the key -- an algebraic way to link the network together.

Exercise. How can the pipes guy try to help the joints guy?

Chains of nodes and chains of edges

We will now approach topology of graphs in a fully algebraic way as the second step in our study of homology theory.

Suppose we are given a graph $G$:

• the set of nodes $N$, and
• the set of edges $E \subset N\times N$, without repetitions. $\\$

We have seen the importance of some special subsets of these sets. First, combinations of nodes may form components:

Second, combinations of edges may form paths (and loops):

In order to deal with these sets, we follow the idea from the last section and impose algebra on vertices and edges in the following very deliberate manner.

Definition. We define chains as formal sums of nodes or edges $$a_1+a_2+...+a_s$$ that follow this cancellation rule: $$x+x=0.$$

It's as if revisiting a node or an edge removes it from consideration...

A chain of edges

• cannot include doubles (such as $AA$), and
• cannot include edges with opposite directions (we assume $AB=BA$), but
• can include repetitions, and
• can include $0$.

Notation: The following notation will be used throughout the book. The set of chains of nodes, or $0$-chains, is: $$C_0=C_0(G):=\Big\{\displaystyle\sum_{A\in Q} A: A \subset N\Big\} \cup \{0\}.$$ The set of chains of edges, or $1$-chains, is $$C_1=C_1(G):=\Big\{\displaystyle\sum_{AB\in P} AB: P \subset E\Big\} \cup \{0\}.$$ These sets include $0$ understood as the chain with all coefficients equal to $0$.

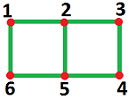
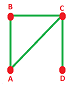
Example. Consider this graph $G$:

• $N=\{A,B,C,D\}$,
• $E=\{AB,BC,CA,CD\}$. $\\$

Its realization is shown below:

Then, $$\begin{array}{llllllll} &C_0 = & \{0,\\ && A,B,C,D,\\ &&A+B,B+C,C+D,D+A,A+C,B+D,\\ &&A+B+C,B+C+D,C+D+A,D+A+B,\\ &&A+B+C+D\},\\ &C_1 = & \{0,\\ && AB,BC,CA,CD,\\ &&AB+BC,BC+CA, ...\}. &\end{array}$$ $\square$

We recognize these as abelian groups. Recall that an abelian group is a set $X$ with a binary operation called addition $$x,y\in X \Longrightarrow x+y\in X,$$ such that

• the addition is associative and commutative;
• it contains the identity element $0\in X$ that satisfies: $x+0=x, \forall x \in X$; and
• it contains the inverse element $-x$ of each $x\in X$ that satisfies $x+(-x)=0$.

Exercise. Prove this conclusion.

In fact, we can rewrite the above groups via their generators: $$\begin{array}{lllll} C_0 = & <A,B,C,D >,\\ C_1 = & < AB,BC,CA,CD >. \end{array}$$ Recall that the rank of an abelian group is the minimal number of its generators. Then, $$\operatorname{rank} C_0=4,\ \operatorname{rank} C_1=4.$$

Definition. The group of chains of nodes(or $0$-chains) of the graph $G$ is given by $$C_0(G)=< N_G >,$$ and the group of chains of edges (or $1$-chains) by $$C_1(G)=< E_G >.$$

If we fix the ordered sets of nodes $N$ and edges $E$ as the bases of these groups, the chains can be written coordinate-wise as column-vectors: $$A=\left[ \begin{array}{llllll} 1\\ 0\\ 0\\ 0 \end{array} \right],\ B=\left[ \begin{array}{lllll} 0\\ 1\\ 0\\ 0 \end{array} \right],\ ...,\ A+B=\left[ \begin{array}{lllll} 1\\ 1\\ 0\\ 0 \end{array} \right], ... $$ We can rewrite these chains of nodes in a more compact way using transposition: $$A=[1,0,0,0]^T,\ B=[0,1,0,0]^T,\ ...,A+B=[1,1,0,0]^T,\ ...;$$ as well as the chains of edges: $$AB=[1,0,0,0]^T,\ BC=[0,1,0,0]^T,\ ...,AB+BC=[1,1,0,0]^T,\ ...$$

The boundary operator

Now, the relation between the edges $E$ and the nodes $N$ is simple:

the two endpoints of an edge are nodes of the graph.

Unfortunately, as there are two nodes $A,B$ for each edge $e$, this relation is not a function $E \to N$. However, these two nodes do form a chain, denoted by $$\partial e=A+B.$$ This is the key step:

the boundary of an edge, $AB$, is a chain of two nodes, $A+B$.

To define a function that will give us all boundaries of all edges of the graph $G$, we set its value for each edge, $AB \in E_G$, first: $$\partial (AB) = A+B.$$ The next step is to extend it to the rest of the chains by “additivity” (or “linearity”): $$\partial (x+y) = \partial (x) + \partial (y).$$ Recall that a function that satisfies this identity “preserves the operations” of the group; i.e., it is a homomorphism. The extension step is simple: $$\partial \Big(\displaystyle\sum _i x_i \Big) = \displaystyle\sum _i \partial (x_i),$$ where $\{x_i\}$ are the edges.

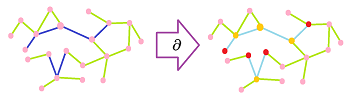
Example. Here is an example of a chain of edges (blue) and its boundary, a chain of nodes (red):

Some nodes appear twice (orange) and are cancelled, also seen in this algebra: $$\begin{array}{llll} \partial (AB +BC+CD)&=\partial (AB)+\partial (BC)+\partial (CD) \\ &= (A+B)+(B+C)+(C+D) \\ &=A+(B+B)+(C+C)+D\\ &=A+0+0+D\\ &=A+D. \end{array}$$$\square$

As a crucial step, for any graph $G$ we have a homomorphism $$\partial = \partial _G: C_1(G) \to C_0(G),$$ called the boundary operator of $G$.

Example. Let's present the boundary operator of the graph from the last section:

We have, of course,

• 1. $\partial (AB)=A+B,$
• 2. $\partial (BC)=B+C,$
• 3. $\partial (CA)=C+A,$
• 4. $\partial (CD)=C+D.$ $\\$

Rewrite these coordinate-wise:

• 1. $\partial \Big([1,0,0,0]^T\Big)=[1,1,0,0]^T$,
• 2. $\partial \Big([0,1,0,0]^T\Big)=[0,1,1,0]^T$,
• 3. $\partial \Big([0,0,1,0]^T\Big)=[1,0,1,0]^T$,
• 4. $\partial \Big([0,0,0,1]^T\Big)=[0,0,1,1]^T$. $\\$

The matrix of $\partial$ uses those as columns: $$D = \left[ \begin{array}{llllll} 1 & 0 & 1 & 0 \\ 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 \end{array} \right].$$ At this point, we (or the computer!) can easily find the boundary of any chain via simple matrix multiplication, as shown here: $$\partial (AB+BC) = \left[ \begin{array}{llllll} 1 & 0 & 1 & 0 \\ 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 \end{array} \right] \left[ \begin{array}{lllll} 1 \\ 1 \\ 0 \\ 0 \end{array} \right]. \begin{array}{lllll} \\ \\ \\ \end{array}$$

$\square$

Exercise. Compute all boundaries of all chains of edges for this graph.

The group of cycles

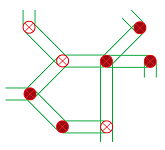
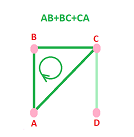
We already know that the issue is challenging because multiple cycles may go around a single hole:

Definition. A $1$-chain is called a $1$-cycle if its boundary is zero. The group of $1$-cycles of graph $G$ is defined to be $$Z_1= Z_1(G):=\{x\in C_1(G): \partial _G x=0\}.$$

Of course, this is simply the kernel of the boundary operator: $$Z_1(G):=\ker \partial _G.$$

Note: “C” in $C_0,C_1$ stands for “chain”, while “Z” in $Z_1$ stands for “Zyklus”, “cycle” in German.

We know that kernels are subgroups. Indeed, a quick proof shows that the kernel is closed under the operations of the group: $$\begin{array}{llllll} x,y \in \ker \partial & \Longrightarrow & \partial (x)=\partial (y)=0 \\ &\Longrightarrow & \partial (x+y)=\partial (x) +\partial (y)=0+0=0 \\ &\Longrightarrow & x+y \in \ker \partial. \end{array}$$ This makes $Z_1$ a subgroup of $C_1$. The “size” of a group is measured by its rank (or, in the language of linear algebra, its dimension).

Example. Some simple algebra is sufficient to find the group of cycles for our example graph:

We use the result above, $\partial (AB +BC+CA)=0$, and a direct examination of $C_1$ to conclude that $$\partial (x)=0 \Longrightarrow x=AB +BC+CA \text{ or } x=0.$$ Hence, $$\begin{array}{llllll} Z_1 &=< AB +BC+CA >=\{0,AB +BC+CA\},\\ \operatorname{rank} Z_1 &=1. \end{array}$$ $\square$

Exercise. Compute $Z_1(G)$ for $G$ the graph with $7$ edges realized as the figure eight.

The group of boundaries

First we realize that

an edge-path from $A$ to $B$ = a chain of edges the boundary of which is $A+B$.

To confirm, consider the next example.

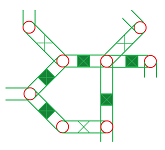
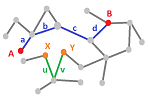
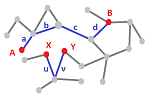
Example. Suppose we are given a graph:

Then, $$\begin{array}{llllll} \partial (a+b+c+d)&=A+B &\Longleftrightarrow &A \sim B,\\ \partial (u+v) &=X+Y &\Longleftrightarrow &X \sim Y. \end{array}$$

But such a chain of edges doesn't have to be a single edge-path. Why not two paths? We can join these two into one chain:

Does this make sense algebraically? Yes: $$\partial (a+b+c+d+u+v)=A+B +X+Y \Longleftrightarrow A +X\sim B+Y.$$ After all, $\partial$ is additive!

A more precise way to understand the result is given by this equivalence: $$\partial (a+b+c+d+u+v)=A+B +X+Y \Longleftrightarrow A +X+ B+Y \sim 0.$$ $\square$

Then, our definition is very simple.

Definition. A $0$-chain is called a $0$-boundary if it is the boundary of some $1$-chain. The group of $0$-boundaries of graph $G$ is defined as $$B_0=B_0(G):=\{P\in C_0(G):\ P=\partial_G(w) \text{ for some } w\in C_1(G) \}.$$

Of course, this definition can be reworded as follows: $$B_0(G):=\operatorname{Im} \partial _G.$$

We know that the images of groups under homomorphisms are subgroups. Indeed, a quick proof shows that this set is closed under the operations: $$\begin{array}{llllll} x,y\in \operatorname{Im} \partial &\Longrightarrow & x=\partial (X),y=\partial (Y)\\ &\Longrightarrow & x+y=\partial (X)+ \partial (Y)=\partial (X+Y) \\ &\Longrightarrow & x+y\in \operatorname{Im} \partial. \end{array}$$

This makes $B_0$ a subgroup of $C_0$.

Example. Let's find the group of boundaries for our example graph:

The group is generated by the values of the boundary operator on the edges, which we have already found: $$\partial (AB)=A+B,\ \partial (BC)=B+C,\ \partial (CA)=C+A,\ \partial (CD)=C+D.$$ We compute: $$\begin{array}{llllll} B_0 &=&< A+B,B+C,C+A,C+D >\\ &=&< A+B,B+C,C+D > \\ &=& \{0,\\ &&A+B,B+C,C+A,C+D,B+D,A+D,\\ &&A+B+C+D\},\\ \operatorname{rank} B_0=3. \end{array}$$ It follows that $\operatorname{rank} C_0-\operatorname{rank} B_0 = 1$. $\square$

Exercise. Modify the above analysis when edge $AD$ is added.

Graph maps

To sort this out, we start with just the nodes.

Example. Let's illustrate the behavior of those continuous functions above that preserve and merge components. We consider two edge-less graphs $G$ and $J$: $$N_G=\{A,B\},\ E_G=\emptyset,\ N_J=\{X,Y,Z\},\ E_J=\emptyset,$$ and define a “function of nodes”: $$f_N:N_G \to N_J$$ by either

• $f_N(A)=X,\ f_N(B)=Y$, or
• $f_N(A)=X,\ f_N(B)=X$. $\\$

$\square$

Next, we need to understand what may happen to an edge under such a “discrete” function.

It is natural to initially assume that the edges are to be taken to edges, by means of some function: $$f_E:E_G \to E_J.$$ Such an assumption doesn't seem to cause any problems; in fact, it matches our basic interpretation of graphs as combinations of “agents” and the relations between them. We simply assign an agent to an agent and a relation to a relation.

However, what about a constant function? What is the discrete counterpart of the function $$f:X\to Y,\ f(x)=y_0\in Y,\ \forall x\in X?$$ An easy answer is to allow an edge to be taken to a node, the event that we will call a “collapse”: $$f(AB)=X \in N_J,\ \forall AB\in E_G.$$

We just learned that a function $f:G\to J$ between graphs should be a combination of two, the node function: $$f_N:N_G \to N_J.$$ and the edge function: $$f_E:E_G \to E_J \cup N_J.$$

Example. Consider two single-edge graphs: $$N_G=\{A,B\},\ E_G=\{AB\},\ N_J=\{X,Y\},\ E_J=\{XY\}.$$ What functions can we define between them?

Let's we assume that $$f_E(AB)=XY.$$ Then we can have several possible values for $A,B$:

• 1. $f_N(A)=X, \ f_N(B)=Y$,
• 2. $f_N(A)=Y, \ f_N(B)=X$,
• 3. $f_N(A)=X, \ f_N(B)=X$,
• 4. $f_N(A)=Y, \ f_N(B)=Y$. $\\$

The first two options make sense because they preserve the relation between the agents. This is not the case for options 3 and 4! By looking at the graphs of these functions (on graphs), we realize that what we accept here is continuity:

and what we reject is the discontinuity:

$\square$

Example. Let's start over with the assumption:

• $f_N(A)=X, f_N(B)=X$. $\\$

The only way to make sense of these is to define the value of the edge to be a node:

• $f_E(AB)=X$.

And for

• $f_N(A)=Y, f_N(B)=Y$, $\\$

we set

• $f_E(AB)=Y$. $\\$

Then we simply have two constant functions here. $\square$

What we have learned is that the values of the function on the nodes dictate the values on the edges, and vice versa.

Keeping in mind that we are after a discrete analog of continuous functions, let's consider another example.

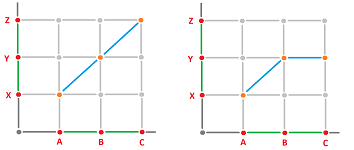
Example. Given two two-edge graphs: $$N_G=\{A,B,C\},\ E_G=\{AB,BC\},\ N_J=\{X,Y,Z\},\ E_J=\{XY,YZ\}.$$ What functions can we define between them?

Consider just these three possibilities:

They are given by these functions:

• (1) $f_N(A)=X, \ f_N(B)=Y, \ f_N(C)=Z, \ f_E(AB)=XY, \ f_E(BC)=YZ$,
• (2) $f_N(A)=X, \ f_N(B)=Y, \ f_N(C)=Y, \ f_E(AB)=XY, \ f_E(BC)=Y$,
• (3) $f_N(A)=X, \ f_N(B)=Y, \ f_N(C)=Z, \ f_E(AB)=XY, \ f_E(BC)=Z$. $\square$

Even a casual look at the graphs reveals the difference: the presence or absence of continuity. In fact, these three graphs look like they could have come from a calculus textbook as illustrations of the issue of continuity vs. discontinuity: $$\lim _{x\to B-} f(x) =f(B) =\lim _{x\to B+} f(x).$$

We need to ensure this kind of continuity. We plot the nodes first and then attach the edges to them. If we discover that this is impossible, no realization of the function can be continuous and it should be discarded.

Therefore, we require from the edge function $f_E$ the following:

• for each edge $e$, $f_E$ takes its endpoints to the endpoints of $f_E(e)$. $\\$

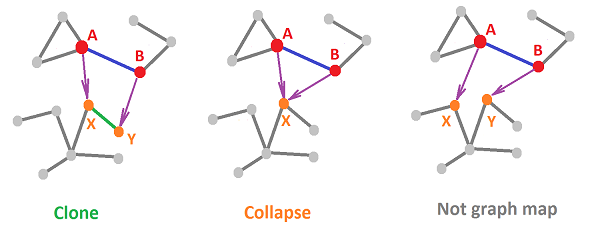
Or, in a more compact form, $$f_N(A)=X, \ f_N(B)=Y \Longleftrightarrow f_E(AB)=XY.$$ We say that, in this case, the edge is cloned.

But what about the collapsed edges? It's easy; we just require:

• for each edge $e$, if $e$ is taken to node $X$, then so are its endpoints, and vice versa. $\\$

Or, in a more compact form, $$f_N(A)=f_N(B)=X \Longleftrightarrow f_E(AB)=X .$$

Definition. A function of graphs $f:G\to J$, $$f=\Big\{f_N:\ N_G\to N_J,\ f_E:E_G \to E_J \cup N_J \Big\},$$ is called a graph map if $$f_E(AB)= \begin{cases} f_N(A)f_N(B) & \text{ if } f_N(A) \ne f_N(B),\\ f_N(A) & \text{ if } f_N(A) = f_N(B). \end{cases}$$

In the most abbreviated form, this discrete continuity condition is: $$f(AB)=f(A)f(B),$$ with the understanding that $XX=X$.

With this property assumed, we only need to provide $f_N$, and $f_E$ will be derived.

Below we illustrate these ideas for general graphs. Here are two continuous possibilities for a discrete function and one discontinuous:

Exercise. Prove that the composition of two graph maps is a graph map.

Exercise. Under what circumstances is there the inverse of a graph map which is also a graph map?

Chain maps

We can now move on to algebra.

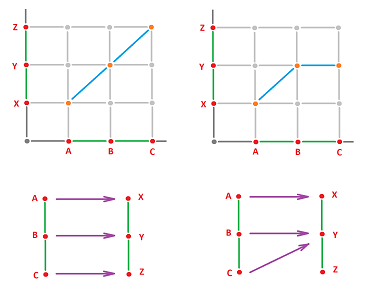
Example. We consider the maps of the two two-edge graphs given above: $$\begin{array}{lll} N_G=\{A,B,C\},& E_G=\{AB,BC\},\\ N_J=\{X,Y,Z\},& E_J=\{XY,YZ\}; \end{array}$$ and the two graph maps.

The key idea is to think of graph maps as functions on the generators of the chain groups: $$\begin{array}{lll} C_0(G)=< A,B,C >,& C_1(G)=< AB,BC >,\\ C_0(J)=< X,Y,Z >,& C_1(J)=< XY,YZ >. \end{array}$$ Let's express the values of the generators in $G$ under $f$ in terms of the generators in $J$.

The first function is given by $$\begin{array}{lllll} &f_N(A)=X,&f_N(B)=Y,&f_N(C)=Z,\\ &f_E(AB)=XY,&f_E(BC)=YZ.& \end{array}$$ It is then written coordinate-wise as follows: $$\begin{array}{lllll} &f_0\Big ([1,0,0]^T\Big)=[1,0,0]^T,&f_0\Big ([0,1,0]^T\Big)=[0,1,0]^T,&f_0\Big ([0,0,1]^T\Big)=[0,0,1]^T,\\ &f_1\Big ([1,0]^T\Big)=[1,0]^T,&f_1\Big ([0,1]^T\Big)=[0,1]^T. \end{array}$$ The second is given by $$\begin{array}{lllll} &f_N(A)=X, &f_N(B)=Y,&f_N(C)=Y,\\ &f_E(AB)=XY,&f_E(BC)=Y. \end{array}$$ It is written coordinate-wise as follows: $$\begin{array}{lllll} &f_0\Big([1,0,0]^T\Big)=[1,0,0]^T, &f_0\Big([0,1,0]^T\Big)=[0,1,0]^T, &f_0\Big([0,0,1]^T\Big)=[0,0,1]^T,\\ &f_1\Big([1,0]^T\Big)=[1,0]^T, &f_1\Big([0,1]^T\Big)=0. \end{array}$$ The very last item requires special attention: the collapsing of an edge in $G$ does not produce a corresponding edge in $J$. This is why we make an algebraic decision to assign it the zero value.

As always, it suffices to know the values of a function on the generators to recover the whole homomorphism. These two functions $f_N$ and $f_E$ generate two homomorphisms: $$f_0:C_0(G) \to C_0(J),\ f_1:C_1(G) \to C_1(J).$$ It follows that the first homomorphism is the identity and the second can be thought of as a projection. $\square$

Exercise. Prove the last statement.

Exercise. Find the matrices of $f_0,f_1$ in the last example.

Exercise. Find the matrices of $f_0,f_1$ for $f:G\to J$ given by $f_E(AB)=XY, \ f_E(BC)=XY$.

Let's take another look at the “discrete continuity conditions” from the last subsection. No matter how compact these conditions are, one is forced to explain that the collapsed case appears to be an exception to the general case. To get around this inconvenience, let's find out what happens under $f$ to the boundary operator of the graph.

Example. We have two here: $$\begin{array}{lll} \partial _G: &C_1(G) \to C_0(G)\\ \partial _J: &C_1(J) \to C_0(J), \end{array}$$ one for each graph.

Now, we just use the fact that $$\partial (AB) = A + B,$$ and the continuity condition takes this form: $$\partial (f_1(AB))=f_0( \partial (AB)).$$ It applies, without change, to the case of a collapsed edge. Indeed, if $AB$ collapses to $X$, both sides are $0$: $$\begin{array}{llllll} &\partial (f_1(AB)) &=\partial (0) &=0;\\ &f_0( \partial (AB))&= f_0( A+B)=f_0(A)+f_0(B)=X+X &=0.&&\square \end{array}$$

We follow this idea and introduce a new concept.

Definition. The chain map generated by a graph map $f:G \to J$ is a pair of homomorphisms $f_{\Delta}:=\{f_0,f_1\}$: $$\begin{array}{lll} f_0:C_0(G) \to C_0(J),\\ f_1:C_1(G) \to C_1(J), \end{array}$$ generated by $f_N$ and $f_E$ respectively.

By design, these two homomorphisms satisfy the following.

Theorem (Algebraic Continuity Condition). For any graph map $f:G \to J$, its chain map satisfies: $$\partial _Jf_1(e)=f_0( \partial _G e),$$ for any edge $e$ in $G$.

Whenever the boundary operator can be properly defined, we can use this condition in any dimension and not just for graphs.

Exercise. Suppose a graph map collapses all edges. Find its chain map.

Exercise. Find the matrix of the chain map of a graph map that shifts by one edge a graph of $n$ edges arranged in (a) a string, (b) a circle.

Exercise. Find the matrix of the chain map of a graph map that folds in half a graph of $2n$ edges arranged in (a) a string, (b) a circle, (c) a figure eight; also (d) for a figure eight with $4n$ edges -- the other fold.

Exercise. Find the matrix of the chain map of a graph map that flips a graph of $2n$ edges arranged in (a) a string, (b) a circle, (c) a figure eight; also (d) for a figure eight with $4n$ edges -- the other flip.

Below are the main theorems of this theory.

Theorem. Transitioning to chain maps preserves the identity: $$(\operatorname{Id}_G)_0={\rm Id}_{C_0(G)},\ ({\rm Id}_G)_1={\rm Id}_{C_1(G)}.$$

Theorem. Transitioning to chain maps preserves the compositions: $$(fg)_0=f_0g_0,\ (fg)_1=f_1g_1.$$

Theorem. Transitioning to chain maps preserves the inverses: $$(f^{-1})_0=f_0^{-1},\ (f^{-1})_1=f_1^{-1}.$$

Exercise. Prove these three theorems.

A wonderfully compact form of the above condition is below: $$\begin{array}{|c|} \hline \\ \quad \partial f=f \partial \quad \\ \\ \hline \end{array} $$ We will see this identity a lot. An appropriate way to describe what happens here is to say that the chain maps and the boundary operators commute. The idea is visualized with so-called “commutative diagrams”.

Commutative diagrams

This very fruitful approach will be used throughout.

Compositions of functions can be visualized as flowcharts:

In general, we represent a function $f : X \to Y$ diagrammatically as a black box that takes an input and releases an output (same $y$ for same $x$): $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccccccc} \text{input} & & \text{function} & & \text{output} \\ x & \ra{} & \begin{array}{|c|}\hline\quad f \quad \\ \hline\end{array} & \ra{} & y \end{array} $$ or, simply, $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} X & \ra{f} & Y. \end{array} $$ Suppose now that we have another function $g : Y \to Z$; how do we represent their composition $fg=g \circ f$?

To compute it, we “wire” their diagrams together consecutively: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccccccc} x & \ra{} & \begin{array}{|c|}\hline\quad f \quad \\ \hline\end{array} & \ra{} & y & \ra{} & \begin{array}{|c|}\hline\quad g \quad \\ \hline\end{array} & \ra{} & z \end{array}$$ The standard notation is the following: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} X & \ra{f} & Y & \ra{g} & Z. \end{array} $$ Or, alternatively, we may want to emphasize the resulting composition: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{rclcc} X & \ra{f} & Y \\ &_{gf} \searrow\quad & \da{g} \\ & & Z \end{array} $$ We say that the new function “completes the diagram”.

The point illustrated by the diagram is that, starting with $x\in X$, you can

• go right then down, or
• go diagonally; $\\$

and either way, you get the same result: $$g(f(x))=(gf)(x).$$

In the diagram, this is how the values of the functions are related: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{rrrlll} &x\in& X &\quad\quad \ra{f} & Y &\ni f(x) \\ &&& _{gf} \searrow \quad& \da{g} \\ &&& (gf)(x)\in & Z &\ni g(f(x)) \end{array} $$

Example. As an example, we can use this idea to represent the inverse function $f^{-1}$ of $f$. It is the function that completes the diagram with the identity function on $X$: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} & X & \quad\ra{f} & Y \\ & & _{{\rm Id}_X} \searrow\quad & \da{f^{-1}} \\ \hspace{.37cm}& & & X&\hspace{.37cm}\square \end{array}$$

Exercise. Plot the other diagram for this example.

Example. The restriction of $f:X\to Y$ to subset $A\subset X$ completes this diagram with the inclusion of $A$ into $X$: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{lccllllllll} & A &\quad \hookrightarrow & X \\ & & _{f|_A} \searrow\quad & \da{f} \\ \hspace{.37cm}& & & Y&\hspace{.37cm}\square \end{array}$$

Diagrams like these are used to represent compositions of all kinds of functions: graph functions, homomorphisms, linear operators, and many more.

Exercise. Complete the diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{cclccc} \ker f & \hookrightarrow & X \\ & _{?} \searrow & \da{f}\\ & & Y& \end{array} $$

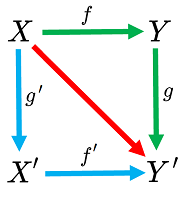
A commutative diagram may be of any shape. For example, consider this square: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{lclccccccc} X & \ra{f} & Y \\ \da{g'} & \searrow & \da{g} \\ X' & \ra{f'} & Y' \end{array} $$ As before, go right then down, or go down then right, with the same result: $$gf = f'g'.$$ Both give you the function of the diagonal arrow!

This identity is the reason why it makes sense to call such a diagram “commutative”. To put it differently,

vertical then horizontal is same as horizontal then vertical.

The illustration above explains how the blue and green threads are tied together in the beginning -- as we start with the same $x$ in the left upper corner -- and at the end -- where the output of these compositions in the right bottom corner turns out to be the same. It is as if the commutativity turns this combination of loose threads into a piece of fabric!

The algebraic continuity condition in the last subsection $$\partial _Jf_1(e)=f_0( \partial _G e)$$ is also represented as a commutative diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{cccccccccc} C_1(G) & \ra{f_1} & C_1(J) \\ \da{\partial _G} & \searrow & \da{\partial _J} \\ C_0(G) & \ra{f_0} & C_0(J). \end{array} $$

Exercise. Draw a commutative diagram for the composition of two chain maps.

Exercise. Restate in terms of commutative diagrams the last two theorems in the last subsection.

Cycles and boundaries under chain maps

Let's review. First, $f$ is a pair of functions:

• 1. $f_N:N_G\to N_J$, and
• 2. $f_E:E_G\to E_J \cup N_J$. $\\$

These two generate the chain map $f_{\Delta}$ of $f$, which is a pair of homomorphisms:

• 1. $f_0:C_0(G)\to C_0(J)$, and
• 2. $f_1:C_1(G)\to C_1(J)$. $\\$

These two “commute” with the boundary operator: $$f_0\partial=\partial f_1 .$$

These homomorphisms reveal what happens to the cycles. First, we have no interest in the $1$-chains that aren't $1$-cycles. That's why we consider the restriction of $f_1$ to the group of cycles $Z_1(G)$: $$f_1\Big|_{Z_1(G)}:Z_1(G)\to C_1(J);$$ it has the same values as the original. Now a crucial step.

Theorem. $f_1$ takes cycles to cycles.

Proof. Suppose $\partial _G(x)=0$, then by the commutativity property above, we have So, we've found the quotient with the generator explicitly presented: $$\hspace{.3in}\partial_J(f_1(x))=f_0(\partial_G(x))=f_0(0)=0.\hspace{.3in}\blacksquare$$

Remember, zero is also a cycle...

So, not only the restriction makes sense but also the values of this new function lie in $Z_1(J)$. Reusing “$f_1$” for this new function, we state this fact as follows.

Corollary. The map of cycles $f_1:Z_1(G)\to Z_1(J)$ is well-defined.

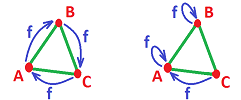
Example. Consider the graph in the form of a triangle: $$N_G=N_J=\{A,B,C\},\ E_G=E_J=\{AB,BC,CA\};$$ and suppose $f$ is this rotation: $$f_N(A)=B, \ f_N(B)=C, \ f_N(C)=A.$$ Its realization is on the left:

A quick computation shows that $$Z_1(G)=Z_1(J)=< AB+BC+CA >.$$ Now, $$\begin{array}{lll} f_1(AB+BC+CA)&=f_1(AB)+f_1(BC)+f_1(CA)\\ &=BC+CA+AB=AB+BC+CA. \end{array}$$ So, $f_1:Z_1(G)\to Z_1(J)$ is the identity (even though $f$ isn't). Conclusion: the hole is preserved.

Now, the other realization is that of the collapse of the triangle onto one of its edges given by $$f_N(A)=A, \ f_N(B)=B, \ f_N(C)=A.$$ Then $$\begin{array}{lll} f_1(AB+BC+CA)&=f_1(AB)+f_1(BC)+f_1(CA)\\ &=AB+BA+0=0. \end{array}$$ So, the homomorphism is zero. $\square$

Exercise. Carry out the “quick computation”.

Exercise. Modify the computations for another rotation and another collapse.