Advanced Topology: exercises

1. List all antiderivatives of $1/x$ and prove, from the definition, that they are continuous.
2. Show that the set of differential forms is a vector space.
3. Prove that $\Omega ^k({\bf R})$ is infinite dimensional.
4. Form the axiomatic definition of differential form, prove that $\Omega^1(p)=span\{dx,dy\}.$
5. Prove that if $\varphi \in \Omega^k$ and $k$ is odd, then $\varphi \wedge \varphi = 0$.
6. Compute (a) $x^2dx^1$ on $<1,2,3>$ at $(3,2,1)$; (b) $dx^1 \wedge dx^3 + x^1dx^2 \wedge dx^4$ on the pair $<-1,0,1,1>, <0,-1,0,1>$ at $ (1,0,0,0)$.
7. Simplify: $$2dx^1 \wedge dx^3 \wedge dx^2 + 3dx^2 \wedge dx^1 \wedge dx^2 - dx^2 \wedge dx^3 \wedge dx^1 .$$
8. Expand and simplify: $$(x^1 dx^2 + x^2 dx^1) \wedge (x^3 dx^1 \wedge dx^2 + x^2 dx^1 \wedge dx^3 + x^1 dx^2 \wedge dx^3).$$
9. Show that a form of even degree commutes with any other form.
10. Find the dimension of the space of differential forms of a point, $\dim \Omega ^k (p) = ?$
11. Provide explicit formulas of the basic forms in $\Omega ^2({\bf R}^3)$, i.e., $dxdy,dydz,dzdx$ in terms of the axiomatic definition. Suggest a formula for the general case of $\Omega ^k({\bf R}^n)$.
12. Compute the exterior derivative of $xydx \wedge dy + yz dy \wedge dz + dz \wedge dx$.
13. To solve the differential equation $$\frac{dy}{dx} = \frac{f(x)}{g(y)}$$ one uses "separation of variables" $$g(y)dy = f(x)dx.$$ Explain the relation between these two equations.
14. Compute $df$, where $f=x^1+2x^2+...+nx^n$, on $<1,-1,...,(-1)^{n-1}>$ at $(1,2,...,1)$.
15. Prove that in ${\bf R}^n$, $$df^1 \wedge ... \wedge df^n(x) = \det \frac{\partial f^i}{\partial x^j}(x)dx^1 \wedge ... \wedge dx^n.$$
16. Write the form $df$, where $f(x) = (x^1) + (x^2)^2 + ... + (x^n)^n$, as a combination of $dx^1,...,dx^n$.
17. Suppose $\alpha, \beta, \gamma \in \Omega ^1({\bf R}^3)$ are linearly independent. Assuming $dd(\alpha)=dd(\beta)=dd(\gamma)=0$, prove that $dd(\psi ^1)=0$.
18. A set $Y \subset {\bf R}^n$ is called star-shaped if there is $a\in Y$ such that for any $x \in Y$ the segment from $x$ to $a$ lies entirely within $Y$. Prove that any two continuous functions $f,g:\rightarrow Y$ are homotopic.
19. Given that the 2nd de Rham cohomology of the sphere is $1$-dimensional: $\Omega^2_{dR}({\bf S}^2)={\bf R}$, list the cohomology classes of the sphere. No proof required.
20. Prove that the boundary of a boundary is zero, in dimension $2$.
21. Show that any $(k−1)$-dimensional face of a $(k+1)$-dimensional cube $Q$ is a common face of exactly two $k$-dimensional faces of $Q$.
22. Two graphs $(V_1, E_1)$ and $(V_2, E_2)$ are equivalent if there exists a bijection $f : V_1 \rightarrow V_2$ such that, for any $u, v \in V_1$, we have $(u, v) \in E_1$ if and only if $(f(u), f(v)) \in E_2$.
23. Prove that any graph that is a tree can be represented as a one-dimensional cubical complex $X$ in the sense that it is equivalent to the graph $(K_0(X), E(X))$, where $E(X)$ are pairs of vertices of edges in $K_0(X)$. Give an example of a graph that cannot be represented by a one-dimensional cubical complex.
24. Let $Q_d$ be a cube and let $X$ be its one-dimensional skeleton, that is, the union of all edges of $Q_d$. For $d = 2, 3, 4, 5, 6$, determine the number of vertices of $Q_d$ and the number of edges of $Q_d$ (note that $X$ has the same vertices and edges as $Q_d$).
25. Use discrete differential forms to describe population growth.
26. For discrete forms in ${\bf R}^3$ compute: (a) $dx \wedge dy$; (b) $dx \wedge \psi ^2$, where the latter is equal to $1$ on a single square, say $\alpha$, parallel to the $xy$-plane and equal to $0$ elsewhere.
27. Compute the exterior derivative of the following form:
    
28. Simplify: $(a)\, 2dxdydz+3dydxdz-dydxdz,(b)(x^1dx^2+x^2dx^2)(x^2dx^1dx^2+x^2dx^1dx^3+x^1dx^2dx^3).$
29. Prove that $dx_{i_1}...dx_{i_{k}}=0$ if and only if $i_{s}=i_{r}$ for some $s\ne r$.
30. (a) Define discrete differential forms for the triangular grid on the plane. (b) Define the exterior derivative of $0$- and $1$-forms and prove that $dd=0$.
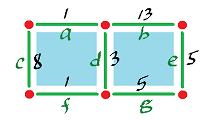
31. (a) Describe the vector spaces of discrete differential forms for the complex:
    
32. Evaluate the cohomology of the complex above (just the answer).
33. (a) Given a smooth function $F:{\bf R}\rightarrow{\bf R}$, what happens to the forms $1,dx$ under $F$? Hint: you can think of $F$ as a change of variables. (b) Given a smooth function $F:{\bf R}^2\rightarrow{\bf R}^2$, what happens to the forms $1,dx,dy,dxdy$ under $F$? (c) Given a function $F:R_1\rightarrow R_2$, what kind of function does $F$ generate between $\Omega^{k}(R_1)$ and $\Omega^{k}(R_2)$?
34. Prove that the following is or is not a (smooth) $2$-manifold: (a) point, (b) circle, (c) torus, (d) ${\bf R}^3$.
35. Evaluate $\int_{C}dx+dy$, where $C$ is the upper half of the unit circle oriented counter-clockwise.
36. Suppose $d:\Omega ^{k}({\bf R}^2)\rightarrow \Omega ^{k+1}({\bf R}^2)$ is the exterior derivative. Suppose $D:\Omega ^{k}(R^2)\rightarrow\Omega ^{k+1}({\bf R}^2)$ is an "alternative" exterior derivative; it satisfies the following: (a) the linearity, (b) the Product Rule, and (c) $DD=0$. Assume that $D=d$ on $\Omega^0({\bf R}^2)$ and prove that $D=d$ on $\Omega^1({\bf R}^2)$.
37. Define wedge product of forms. Give examples. State and prove the skew commutativity property.
38. Prove $dd=0$ for smooth $0$-forms.
39. Define de Rham cohomology. Give examples.
40. Define simple connectedness. Give examples. State the theorem about the closed and exact forms on a simply connected region in the plane.
41. Define discrete forms in the plane. Give $dx,dy,dxdy.$
42. Define the Hodge $\star$ operator for discrete forms on the plane. Give examples.
43. Compute $d(Fdx+Gdy)$ for discrete forms in the plane.
44. Define smooth manifolds. Give examples and non-examples.
45. Define orientation of $0$- and $1$-manifolds.
46. How do you construct a cochain from a smooth form?
47. Prove that $\int _{-C} \psi = \int _C \psi$ for $1$-forms.
48. State the general Stokes theorem. Give applications.
49. Draw the Mobius band in the 3D grid.
50. Using row operations compute the cohomology of the following complexes:
    1. 
    2. 
51. Show that the set of differential forms is a vector space.
52. Compute (a) $x^2dx^1$ on $<1,2,3>$ at $(3,2,1)$; (b) $dx^1 \wedge dx^3 + x^1dx^2 \wedge dx^4$ on the pair $<-1,0,1,1>, <0,-1,0,1>$ at $ (1,0,0,0)$.
53. Simplify: $$2dx^1 \wedge dx^3 \wedge dx^2 + 3dx^2 \wedge dx^1 \wedge dx^2 - dx^2 \wedge dx^3 \wedge dx^1 .$$
54. Compute the exterior derivative of $xydx \wedge dy + yz dy \wedge dz + dz \wedge dx$.
55. Suppose $\alpha, \beta, \gamma \in \Omega ^1({\bf R}^3)$ are linearly independent. Assuming $dd(\alpha)=dd(\beta)=dd(\gamma)=0$, prove that $dd(\psi ^1)=0$.
56. Given that the 2nd de Rham cohomology of $3$-space with a point removed is $1$-dimensional: $\Omega^2_{dR}({\bf R}^3-\{0\})={\bf R}$, list its cohomology classes. No proof required.
57. Prove that the boundary of a boundary is zero, in dimension $2$ (for cubical complexes).
58. For discrete forms in ${\bf R}^3$ compute: (a) $dx \wedge dy$; (b) $dx \wedge \psi ^2$, where the latter is equal to $1$ on a single square, say $\alpha$, parallel to the $xy$-plane and equal to $0$ elsewhere.
59. Compute the exterior derivative of the following form:
    
60. (a) Describe the vector spaces of discrete differential forms for the complex:
    
    (b) Evaluate the cohomology of the complex above (just the answer).
61. A set $Y \subset {\bf R}^n$ is called star-shaped if there is $a\in Y$ such that for any $x \in Y$ the segment from $x$ to $a$ lies entirely within $Y$. Prove that any two continuous functions $f,g:X\rightarrow Y$ are homotopic, for any $X$.
62. How do you construct a cochain from a continuous form?
63. Construct the dual cubical complex of the cubical complex of the figure 8 (the one with 7 edges).
64. For discrete forms in ${\bf R}^3$ compute: (a) $dx \wedge dy$; (b) $dx \wedge \psi ^2$, where the latter is equal to $1$ on a single square, say $\alpha$, parallel to the $xy$-plane and equal to $0$ elsewhere.
65. Using row operations compute the homology (or cohomology) of the one pixel complex: .
66. Let $K$ be the cubical complex of $[0,1]$ and let $L$ be the complex of $\{0,1\}$. Compute $C_1(K)/C_1(L)$. What is the meaning of what you've found?
67. Provide a cubical complex equipped with a metric tensor -- for a hollow cube.
68. State the continuous Poincare Lemma along with all necessary definitions.
69. Give examples of forms that are closed but not exact, both continuous and discrete.
70. Explain the Fundamental Correspondence (between forms and functions/vector fields).
71. Assuming that the Hodge duality of cells is already given define Hodge duality of forms.