This site is being phased out.
Topological spaces
Contents
Open and closed sets
In order to define and study
- continuity,
- path-connectedness,
and other related issues, all we need is to equip each of the sets involved with an additional structure called topology.
Definition. Given an arbitrary set $X$, a collection $\tau$ of subsets of $X$ is called a topology on $X$ if it satisfies the following conditions:
- (T1) $\emptyset, x \in \tau$;
- (T2) if $\alpha \subset \tau$ then $\cup \alpha \in \tau$;
- (T3) if $U,V \in \tau$ then $U \cap V \in \tau$.
The pair $(X,\tau)$ is called a topological space. The elements of $\tau$ are called open sets.
Of course, instead, we can, and did, start with the set of all neighborhoods $\gamma$ in $X$ and then define open sets as ones where every point has its own neighborhood: a subset $W$ of $X$ is called open (with respect to $\gamma$) if for any $x$ in $W$ there is a neighborhood $U$ ($\in \gamma$) of $x$ that lies entirely within $W$:
Then, as we have proven, the set of all such sets, say $\tau _{\gamma}$, satisfies (T1)-(T3).
We will use both approaches, whichever is more convenient at the time.
As an example, all “open”, as we have known them, intervals, finite or infinite, are open in ${\bf R}$: $$(0,1),..., (0, \infty ), (- \infty ,0),...$$
“Open” disks on the plane, and balls in the Euclidean space, are also open.
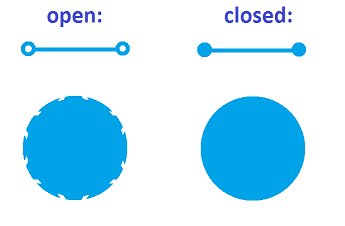
Definition. A subset is called closed if its complement is open.
For example all “closed” intervals, finite or infinite, are closed in ${\bf R}$: $$[0,1],..., [0, \infty ), (- \infty ,0],...$$
“Closed” disks on the plane, and “closed” balls in the Euclidean space are also closed. Points too.
There is a standard way to visualize open vs. closed sets. For the former, the borders are drawn “hollow” in order to suggest that they are not included for both dimensions $1$ and $2$:
Some sets are neither closed nor open (unlike doors!). Examples in ${\bf R}$ are half-open intervals: $[0,1),$ and convergent sequences: $$S=\left\{ \frac{1}{n}:\ n=1,2, ... \right\}$$ that don't include their limit.
To see that the latter is neither (with respect to the standard Euclidean topology), consider these two facts:
- $x=1$ does not have an interval around it that lies entirely inside an open $S$, $\quad \Rightarrow $ not open;
- $x=0$ is in the complement of $S$ but it does not have an interval around it that lies inside in ${\bf R} \setminus S$, $\quad \Rightarrow $ not closed.
However, $S \cup \{0 \}$ is closed.
Theorem. The set $\sigma$ of all closed sets satisfies the following conditions:
- (T1') $\emptyset, X \in \sigma$;
- (T2') if $\alpha \subset \sigma$ then $\cap \alpha \in \sigma$;
- (T3') if $P,Q \in \sigma$ then $P \cup Q \in \sigma$.
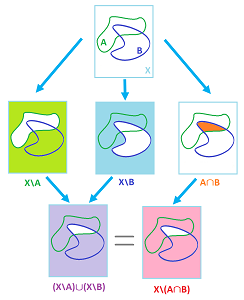
Proof. (T3') follows from (T3), illustrated below:
We simply used the de Morgan's Laws.
[math]\blacksquare[/math]
Exercise. Given a basis of neighborhoods $\gamma$, prove directly, i.e., without using the de Morgan's Laws, that the set $\sigma _{\gamma}$ of all closed sets with respect to $\gamma$ satisfies (T1')-(T3'). Hint: imitate the proof for $\tau _{\gamma}$.
Of course, condition (T3') implies that the union of any finite collection of closed sets is closed.
To see why the (T3') cannot be extended to infinite collections of sets, consider these examples: $$\bigcap \left\{\left( -\frac{1}{n}, \frac{1}{n}\right):\ n = 1,2, … \right\} = \{0 \};$$ $$\bigcup \left\{\left[-1 + \frac{1}{n}, 1 - \frac{1}{n}\right] :\ n = 1,2, … \right\} = (-1,1).$$
So, just as there is no (T3) for closed sets, there is no (T3') for open sets.
A note on terminology. Once we assume that the topology $\tau$ is fixed, all references to it will be routinely omitted. Instead of a topological space $(X,\tau)$, we will speak of a topological space $X$, along with some assumed fixed $\tau$, and
- “open sets in $X$” = the elements of $\tau$,
- “closed sets in $X$” = the complements of the elements of $\tau$,
- “neighborhoods of points in $X$” = the elements of some fixed basis $\gamma$ that generates $\tau$.
A profound (but not unexpected) benefit of limiting yourself to using only the language of open sets is that all properties you are able to discuss are intrinsic! They are called topological invariants.
Proximity of a point to a set
There are no measurements in topology. Does the distance between a point and a set make any sense?
Let's just try to decide if the distance is $0$ or not.
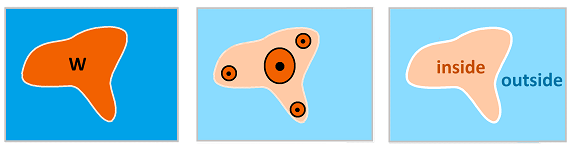
Suppose we are given a subset $A$ of a topological space $X$. We can state, without hesitation, that, if $x\in A$, then the distance between them is $0$!
Now, for $X:={\bf R}$, suppose $A$ is the set of points of the sequence $$A:=\left\{ \frac{1}{n}:\ n=1,2... \right\}.$$ What is the distance between $A$ and $0\not\in A$? Since the sequence converges to this point, the distance also appears to be $0$! But the distance to $-1$ can't be $0$.
What makes a difference topologically? There is a neighborhood of $-1$, or any number $x<0$, that separates it from the set $A$. That's what makes it “far from” $A$.
This idea of separation of a point from a set, or from its complement, is developed below.
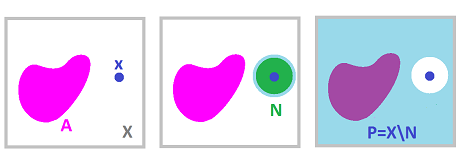
Definition. A point $x\in X$ is called an interior point of $A$ if there is a neighborhood $W$ of $x$ that lies entirely in $A$. The set of interior points of a set is called its interior denoted by: $$\operatorname{Int}(U).$$
In other words, these are the points that are “far from” $X \setminus A$ as each is isolated from the complement of $A$ by a neighborhood.
Then an open set $U$ coincides with its interior. In fact, we have the following:
Theorem. $\operatorname{Int}(A)$ is open for any $A$.
Example. The interior points of $A = [0,1]$ in ${\bf R}$ are $(0,1)$. Same for $(0,1], [0,1)$, and $(0,1)$.
In ${\bf R}^2$, let
- $A := \{(x,y): x^2+ y^2 \leq 1 \}$ (the closed disk), then
- $\operatorname{Int}(A) = D = \{(x,y): x^2 + y^2 < 1 \}$ (the open disk); also
- $\operatorname{Int}(D) = D.$
$\square$
Example. The interior of a circle $C = \{(x,y): x^2 + y^2 = 1 \}$ in the plane is empty. $\square$
Definition. A point $x$ is called an exterior point of $A$ if there is a neighborhood $W$ of $x$ that lies entirely in $X \setminus A$. We will use notation $$\operatorname{Ext}(A)$$ for this set called the exterior.
These are the points that are “far from” $A$.
In other words, exterior points are interior points of the complement.
Example. In ${\bf R}$, suppose $P$ is the set of point of the sequence $$P:=\left\{ \frac{1}{n}:\ n=1,2... \right\}.$$ Then the exterior points of $P$ are all points in the complement of $P$ except for $0$. Why not $0$? Because $\frac{1}{n}\to 0$; hence, for any $\epsilon >0$ there is a large enough $n$ so that $\frac{1}{n} \in B(0, \epsilon)$. Also, $\operatorname{Int}(P)$ is empty. $\square$
Definition. A point $x$ is called a limit point of $A$ if for any neighborhood $W$ of $x$ $$W \cap A \neq \emptyset.$$
Certainly, $0$ is a limit point for the set $P$ above. But also note that any point $x$ in $A$ is a limit point of $A$ since $x \in W \cap A$. To exclude this possibility and to be able to study convergence of sequence in sets, we introduce one more notion.
Definition. A point $x$ is an accumulation point of $A$ if for any neighborhood $W$ of $x$ $$W \cap (A \setminus \{x\}) \neq \emptyset.$$
A point $x$ that is a limit point but not an accumulation point of $A$ satisfies: there is a neighborhood $W$ of $x$ such that $$W \cap A = \{x\}.$$
Definition. A point $x$ in a set $A$ is called isolated if there is a neighborhood $W$ of $x$ the intersection of which with the set $A$ is $\{x \}$.
Example. Suppose $Q$ is the set that consists of the points of the same sequence as above but combined with its limit, $0$: $$Q:=\left\{ \frac{1}{n}:\ n = 1,2... \right\} \cup \{0\}.$$ Then all points of $Q$ are isolated except for $0$. $\square$
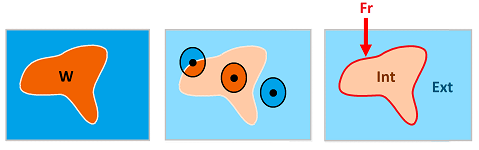
Definition. A point $x$ is called a frontier point of $A$ if it is a limit point for both the set $A$ and its complement. The set of all frontier points is called the frontier $\operatorname{Fr}(A)$ of subset $A$.
The condition can be restated as: any neighborhood $W$ of $x$ intersects both $A$ and $X \setminus A$.
Example. The frontier $\operatorname{Fr}(D)$, of the open disk $A$ is the circle $C$. $\square$
The frontier is not to be confused with the boundary even though they are sometimes equal.
Given a subset $A$ of a topological space $X$, all points of $X$ can now be classified according to how close they are to $A$ and to its complement.
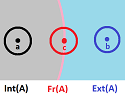
Interior - frontier - exterior
Theorem. For any set $A$ in $X$, the interior, the frontier, and the exterior of $A$ form a partition of $X$: $$X=\operatorname{Int}(A) \sqcup \operatorname{Fr}(A) \sqcup \operatorname{Ext}(A).$$
Proof. We want to show that the complement of the union of the interior and exterior consists of all points that are limit points of both $A$ and its complement. This is just a matter of manipulating the definitions in a predictable way:
Suppose $\gamma$ is the basis of neighborhoods. Then
- (1) $a\in \operatorname{Int}(A) \Leftrightarrow \exists N_a\in \gamma, N_a\subset A$;
- (2) $b\in \operatorname{Ext}(A) \Leftrightarrow \exists N_a\in \gamma, N_b\subset X\setminus A$.
Now,
- $x\in\operatorname{Int}(A) \cup \operatorname{Ext}(A) \Leftrightarrow $
- (1) $\exists N_a\in \gamma,x\in N_a,N_a\subset A$; OR
- (2) $\exists N_b\in \gamma,x\in N_b,N_b\subset X\setminus A$.
Therefore, a point is in the complement if and only if it satisfies the negation of (1) and (2):
- $c\notin \operatorname{Int}(A) \cup \operatorname{Ext}(A) \Leftrightarrow c\in X\setminus(\operatorname{Int}(A) \cup \operatorname{Ext}(A))= (X\setminus \text{Int}(A)) \cap (X\setminus \operatorname{Ext}(A))\Leftrightarrow$
- (1') $\forall N_c\in \gamma, N_c\cap A \ne \emptyset$; AND
- (2') $\forall N_c\in \gamma, N_c\cap X\setminus A \ne \emptyset$;
Putting these two together:
- $c\notin \operatorname{Int}(A) \cup \operatorname{Ext}(A) \Leftrightarrow $
- $\forall N_c\in \gamma, N_c\cap A \ne \emptyset$ and $N_c\cap (X\setminus A) \ne \emptyset$.
$\blacksquare$
Definition. The closure, $\operatorname{Cl}(A)$, of $A$ is the set of all limit points of $A$.
The following two theorems are obvious:
Theorem. $$\operatorname{Int}(A) \subset A \subset \operatorname{Cl}(A).$$
Theorem. $$\operatorname{Cl}(A) = \operatorname{Int}(A) \cup \operatorname{Fr}(A).$$
Theorem.
- 1. $\operatorname{Int}(A)$ is open.
- 2. $\operatorname{Fr}(A)$ is closed.
- 3. $\operatorname{Cl}(A)$ is closed.
Proof. (1) is obvious. (2) and (3) below. $\blacksquare$
To summarize these definitions, let's consider the gaps in this sentence for $x\in A$, and the three ways they can be filled:
$$\begin{array}{c|c|c|c|c} \text{“If } \exists W_x \text{ so that} & ... & , x \text{ is an} & ... & \text{point.”}\\ \hline ... & W_x \subset A & ... & \text{interior} & ... \\ ... & W_x \subset X \setminus A & ... & \text{exterior} &...\\ ... & W_x \cap A =\{x\} & ... & \text{isolated} &... \end{array}$$
Now consider another sentence, for $x\in A$, with gaps and the three ways they can be filled:
$$\begin{array}{c|c|c|c|c} \text{“If } \forall W_x \text{we have} & ... & , x \text{ is a} & ... & \text{point.”}\\ \hline ... & W_x \cap A \neq \emptyset & ... & \text{limit} & ... \\ ... & W_x \cap (A\setminus \{x\}) \neq \emptyset & ... & \text{accumulation} & ... \\ ... & W_x \cap A \neq \emptyset, W_x \cap (X \setminus A) \neq \emptyset & ... & \text{frontier} &... \end{array}$$
Theorem.
- (1) The closure is the intersection of a certain collection of closed sets. $\Rightarrow$
- (2) The closure is closed. $\Rightarrow$
- (3) The frontier is closed.
It follows from this result/.
Theorem. The closure of a set is the smallest closed set containing the set: $$\operatorname{Cl}(A)=\bigcap \{G: G \text{ closed in } X,A\subset G\}.$$
Proof. Let $$\begin{array}{ll} \alpha := &\{G: G \text{ closed in } X,A\subset G\},\\ \bar{A}:= &\cap \alpha. \end{array}$$ Then we need to show
- $\bar{A} = \operatorname{Cl}(A)$.
A proof of equality will often contain two parts:
- 1. $\bar{A} \subset \operatorname{Cl}(A)$, and
- 2. $\bar{A} \supset \operatorname{Cl}(A)$.
Part 1. We start on the right. Suppose $x \notin \operatorname{Cl}(A)$. Then, by definition, $x$ is not a limit point of $A$, so
- there is an open neighborhood $N$ of $x$ such that
- $N \cap A =\emptyset$.
Now, we need to connect $N$ to $\bar{A}$ and, hence, to $\alpha$. But the latter consists of closed sets, while $N$ is open! So, let's try $$P:=X\setminus N.$$ This clever idea is illustrated below:
Observe:
- $P$ is closed because $N$ is open, and
- $P$ contains $A$ because $N \cap A = \emptyset$.
Therefore, $P\in \alpha$. It follows that $$\bar{A}=\cap \alpha \subset P.$$ Hence, $x \notin \bar{A}$.
To summarize what has been proven, $$x \notin \operatorname{Cl}(A) \Rightarrow x \notin \bar{A}.$$ Finally, we rephrase this as: $$\operatorname{Cl}(A) \supset \bar{A}.$$ Note: except for choosing to consider $P$, the proof can be seen as routine and based entirely on the definition.
$\blacksquare$
Exercise. Prove: $$\bar{A} \supset \operatorname{Cl}(A).$$
Exercise. Prove: $$\operatorname{Cl}(A \cap B) \subset \operatorname{Cl}(A)\cap \operatorname{Cl}(B).$$ What if there are infinitely many sets?
Theorem. The interior of a set is the largest open set contained by the set: $$\operatorname{Int}(A)=\bigcup \{U: U \text{ open in } X,A\supset G\}.$$
Exercise. Prove this theorem based entirely on the definition, just as the last theorem.
Exercise. Prove: $$\overline{B(p,d)}=\bar{B}(p,d).$$
Convergence of sequences
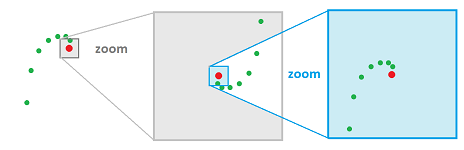
Recall from calculus that a sequence of numbers $\{x_n:\ n=1,2,...\}$ converges to number $a$ if for any $\epsilon >0$ there is $N>0$ such that for any integer $n>N$ we have $$|x_n-a|<\epsilon.$$ In other words, the elements of the sequence will be eventually within $\epsilon$ from $a$. In the case of an $m$-dimensional Euclidean space, the last part will be $$||x_n-a||<\epsilon,$$ with the norm $|| \cdot ||$ replacing the absolute value.
This idea is visualized through a repeated zooming in on the “tail” of the sequence:
Based on our experience with continuity, we know how to recast this definition in terms of bases of neighborhoods. We just observe that the last past is simply: $$x_n\in B(a,\epsilon ),$$ with the latter set an element of the Euclidean basis. In other words, the elements of the sequence will be eventually within $U=B(a,\epsilon )$ from $a$. Finally, we just replace the standard Euclidean neighborhood with one of arbitrary nature, as follows.
Definition. Suppose $X$ is a set with a basis of neighborhoods $\gamma$. Suppose also $\{x_n:\ n=1,2,...\}$ is a sequence of elements of $X$ and $a\in X$. Then we say that the sequence converges to $a$, $$\lim _{n \to \infty} x_n =a \text{, or }$$ $$x_n\to a \text{ as } n\to \infty,$$ if for any $U\in \gamma$ there is $N>0$ such that $$n>N \Rightarrow x_n\in U.$$
Exercise. Prove that the definition is remains equivalent if we replace “basis $\gamma$” with “topology $\tau$”.
Since squares refine disks, every convergent (in the usual sense) sequence in ${\bf R}^2$ will also converge with respect to the squares.
Exercise. Prove that if $x_n\to a$ then $(x_n,0) \to (a,0)$:
Exercise. Show that if a sequence converges with respect to a basis $\gamma$, it also converges with respect to any basis equivalent to $\gamma$.
Let's consider convergence in the two extreme cases: discrete and anti-discrete.
Example. When do we have $x_n\to a$ in discrete topology? So many choices for $U$... Let's try $U:=\{a\}$! Then $x_n\in U$ means simply that $x_n=a$. So, the only sequences that converge to $a$ are those that are equal to $a$, eventually:
- $x_1,x_2,...,x_k,a,...,a,...$ converges to $a$; however
- $1,1/2,1/3,...,1/n,...$ diverges.
$\square$
Example. When do we have $x_n\to a$ in anti-discrete topology? There is only one choice for us, $U:=X$! But then $x_n\in U$ means that there is no restriction whatsoever. Consequently, all sequences converge to all points -- at the same time. Yes, even this one: $$\lim _{n\to \infty}1= 0.$$ $\square$
Just as the analysis of path-connectedness in the last section, these examples are intended to demonstrate how little we can rely on intuition and visualization at this level of abstraction. This also sets the standard of proof in point-set topology.
Exercise. What condition on the topology of $X$ would guarantee the uniqueness of limits?
Theorem. Continuous functions preserve convergence: if $f:X\to Y$ is a continuous function and $x_n\to a$ as $n\to\infty$ in $X$, then $f(x_n)\to f(a)$ as $n\to\infty$ in $Y$.
Exercise. Prove the theorem.
Exercise. Given a sequence $\alpha = \{x_n:\ n=1,2,...\}$ in a topological space $X$. View the sequence as a subset $A = \{x_n:\ n\in{\bf N} \}$ of $X$ and compare the meanings of the limit points of $A$ and the accumulation points of $A$. What about the limit of $\alpha$?
Exercise. Suppose we have a set $X$. Suppose also a collection $\alpha$ of sequences in $X$ is given and each sequence $q$ in $\alpha$ is associated with a point $x_q\in X$. What is an appropriate topology for $X$? Construct a topology on $X$ such that $p\to x_p$ for any $p\in \alpha$ and the rest diverge. Hint: what restrictions on $\alpha$ would guarantee that this is possible?
Metric spaces
Notice that, in the Euclidean space, convergence of points $$x_n\to a$$ simply means convergence of certain numbers, $$||x_n-a||\to 0.$$ In other words, the distance from $x_n$ to $a$ converges to $0$, in ${\bf R}$. So, in a given topological space, we can capture convergence of its sequences if we can find an appropriate distance function.
Definition. Given a set $X$, any function $$d: X \times X \to {\bf R}$$ is called a metric (or a “distance function”) if it satisfies the following conditions, for every $x,y,z \in X$,
- (M1) positivity: $d(x,y) \geq 0$, with equality if and only if $x=y$;
- (M2) symmetry: $d(x,y) = d(y,x)$;
- (M3) triangle inequality: $d(x,z) \leq d(x,y) + d(y,z)$.
In this case, the pair $(X,d)$ is called a metric space.
For $a \in X$ and $\epsilon > 0$, the open ball around $a$ of radius $\epsilon$ is the set $$B(a,\epsilon) := \{x \in X :\ d(x,a) < \epsilon\}.$$ These sets form a basis of neighborhoods $\gamma _m$ for $X$. Indeed, (B2) follows from (M3). Then the topology on $X$ generated by $\gamma _m$, or any other metric, is called a metric topology.
The Euclidean space ${\bf R}^n$ is a metric space with the metric defined by $$d(x,y)= d_E(u,v):= ||u-v||.$$
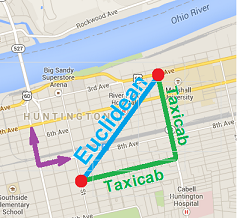
Example (taxicab metric). Let's compare the Euclidean metric on the plane, $$d_E(u,v):= \sqrt{|u_1-v_1|^2+|u_2-v_2|^2}$$ to the taxicab metric (aka “Manhattan metric”). To find the distance between the vectors we go along the grid: $$d_M(u,v):= |u_1-v_1|+|u_2-v_2|.$$
Taxicab's circle is a square... and, as we know, the squares generate the same topology as the disks: the geometry is different but the topology is the same!
$\square$
Exercise. The post office metric is based on the idea that postman's has to go through the post office. Find the formula and prove that this is a metric.
The discrete topology is generated by this trivial metric: $$d_D(x,y):=\begin{cases} 1 & \mbox{if } x \ne y, \\ 0 & \mbox{if } x = y. \end{cases}$$ However, the anti-discrete topology (with more than one point) cannot be generated by a metric!
Exercise. Suppose $d$ is a metric on $X$. Prove that the function $d_1:X\times X\to {\bf R}$ given by $$d_1(x,y):=\min\{d(x,y),1\}$$ is also a metric. Are they equivalent?
Spaces of functions
Notation. Let $C(X)$ stand for the set of all continuous functions on $X$.
Consider $C[a,b]$,the set of all continuous functions $f:[a,b]\to {\bf R},\ b>a$.
One may equip this set with a variety of topologies, starting with discrete and anti-discrete. However, the main meaningful examples come from the two primary ways sequences of functions may converge.
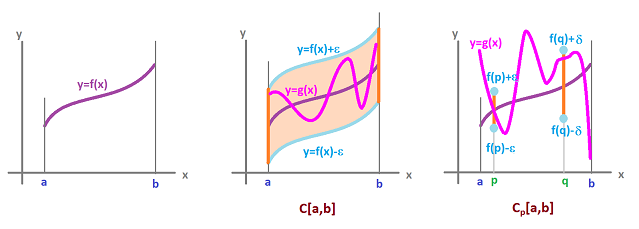
The first is the uniform convergence: a sequence $f_n\in C[a,b],\ n=1,2,...,$ uniformly converges to $f$ if $$\max_{x\in [a,b]}|f_n(x)-f(x)|\to 0.$$ This convergence is produced by the sup-metric (or sup-norm) on $C[a,b]$: $$d_S(f,g):=\max_{x\in [a,b]}|f(x)-g(x)|.$$ The picture below (middle) shows an $\epsilon$-neighborhood of $f$: a function $g$ can behave arbitrarily as long as it stays within the “tunnel” with these two “walls”: $y=f(x)-\epsilon$ and $y=f(x)+\epsilon$.
Exercise. Why is the sup-norm well-defined?
The following result, which we accept without proof, underscores the importance of this topology and the reason why it is the default choice.
Theorem. The uniform limit of continuous functions is continuous.
The second way is the point-wise convergence: a sequence $f_n\in C[a,b],\ n=1,2,...,$ point-wise converges to $f$ if $$|f_n(x)-f(x)|\to 0,\ \forall x\in [a,b].$$ The picture above (right) shows a neighborhood of $f$: a function $g$ can behave arbitrarily as long as it passes through, not a “tunnel”, but a series of “gates”, with these “posts”: $f(p)-\epsilon$ and $f(p)+\epsilon$, $f(q)-\delta$ and $f(q)+\delta$, etc.
Exercise. Explain why the depicted set is a neighborhood.
There can be multiple values of $x$ for which the “gates” are built, with different widths, but not infinitely many! That's why they can't hold the functions as tight as a “tunnel”. There is no metric for this topology.
Example. The point-wise limit of continuous functions doesn't have to be continuous. Just choose: $$a:=0,\ b:=1,\ f_n(x):=x^n,$$ $$f(x):= \begin{cases} 0 &\text {if } x \in [0,1), \\ 1 & \text{if } x = 1. \end{cases}$$ The limit function is discontinuous!
$\square$
Exercise. (a) Prove that uniform convergence implies point-wise convergence. (b) Give an example of a sequence $f_n\in C[a,b]$ with
- $f_n\to f\in C[a,b]$ point-wise, but
- $f_n\not\to f\in C[a,b]$ uniformly.
Exercise. (a) Define a metric on $C[a,b]$ based on the definite integral. (b) Compare it to the uniform and point-wise convergence.
The order topology
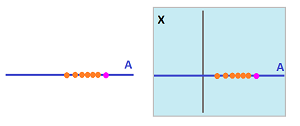
The standard basis of the topology of the reals consists of all open intervals: $$\{(a,b):\ a,b\in{\bf R},a < b\}.$$ But what is an interval? It is a set of all elements in ${\bf R}$ that lie strictly between two given elements of ${\bf R}$. This is not a coincidence: this is how a basis is formed for all partially ordered sets.
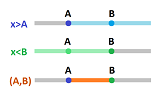
The three types of intervals in a linearly ordered set, such as ${\bf R}$ or ${\bf Z}$, are illustrated below:
What about partially ordered sets? Recall that a partial order is a binary relation “$\le$” between pairs of elements of a set $X$ that satisfies these three axioms:
- 1. reflexivity: $x \le x$;
- 2. antisymmetry: if $x \le y$ and $y \le x$ then $x = y$;
- 3. transitivity: if $x \le y$ and $y \le z$ then $x \le z$.
Of course, we write $x < y$ when $x \le y$ and $x \ne y$. Then $X$ is called a partially ordered set or poset.
Given an order on a set $X$, the basis $\beta$ of topology of $X$ is chosen to be the collection of all intervals of all three types:
- $(A,\infty)=\{x\in X: x > A\}$,
- $(-\infty,B)=\{x\in X: x < B\}$,
- $(A,B)=\{x\in X: x > A, x < B\}$.
It is called the order topology generated by the order.
Exercise. Prove that $\beta$ is a basis.
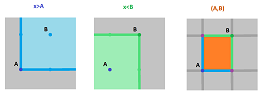
For example, ${\bf R}^2$ and ${\bf Z}^2$ are ordered by:
Consider the three types of intervals in ${\bf R}^2$:
Observe that, except for the points $A,B$ themselves, the (Euclidean) boundaries of these regions are included in the open intervals!
Exercise. Show how “open rays” define the same topology.
Exercise. Define a partial order on $C[a,b]$ and compare the order topology with the sup-metric topology.
Above we used for ${\bf R}^2$ and ${\bf Z}^2$ the product order on the product set $X\times Y$ set of two ordered sets $X,Y$:
Alternatively, this is how the product $X\times Y$ set of two ordered sets $X,Y$ is ordered via the so-called the lexicographical order:
Exercise. Provide the intervals with respect to the lexicographical order on ${\bf R}^2$.
Example. A different kind of ordered set is given by any group of people ordered by genealogical descendancy: $A > B$ if $A$ is a direct descendant of $B$. Then some typical open intervals are:
- (parent, child) $=\emptyset$;
- (grandparent, grandchild) $=\{$parent$\}$;
- (husband, wife) $=\emptyset$;
- (cousin, cousin) $=\emptyset$; etc.
$\square$
Exercise. Given an arbitrary set $X$, let $P$ be any collection of subsets of $X$. Prove that $P$ is partially ordered by inclusion and describe the intervals of its order topology.