Topological features of images

Redirect to:

Topology

Topological issues in image analysis

The following simple questions show the important role played by topology in analysis of digital images and computer vision.

A microchip - very complex structure that is hard to analyze with a naked eye:

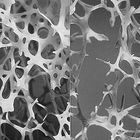
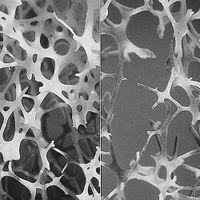
Bone under microscope - a 3D image:

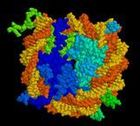
Complex molecule of a protein:

3D structure of an alloy:

How do you teach a computer to

count the number, the shapes, and sizes of components in a microchip?
tell the letter 'P' from the letter 'B' or locate all tunnels in a human bone or a large molecule?
find, count, and measure voids in a piece of alloy or a mixture of two liquids?

And further, how can one extract these features from the image?

Note: It's not too much of a stretch to translate "topology" (from the Greek) as "image analysis"...

Algebraic topology

The way to answer these questions has been known to mathematicians for more than a century. The techniques of algebraic topology, specifically, homology theory, have been available since long before the proliferation of computers and digital imaging. However, homology theory has not been broadly used in the current imaging technology. One of the reasons is that these techniques are only applicable to either “sets” or "cell complexes".

From the point of view of image processing, these are binary still images. It is, therefore, our goal to make algebraic topology applicable to, first, gray scale and color images and, second, video sequences. But we start with binary images.

Homology theory can answer the questions above by finding explicit, algebraic representations called homology classes of the necessary topological features of the image. Specifically, for each of the three situations above, one finds these classes in the appropriate dimensions:

objects or connected components – dimension 0,
holes or tunnels – dimension 1, and
voids or cavities – dimension 2.

The numbers of (algebraically independent) homology classes in each dimension are called the Betti numbers, $B_0, B_1, B_2$. Simple examples are given in the table below.

	$B_0$ (parts)	$B_1$ (holes)	$B_2$ (voids)
Letter 'O'	1	1	0
Two letters 'O'	2	2	0
Letter 'B'	1	2	0
Donut	1	1	0
Tire	1	2	1
Ball	1	0	1

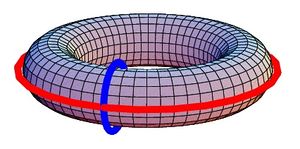
The torus (tire) has two tunnels captured by these two "cycles". In case of a donut the blue one does not count because it can be contracted (is "homologous") to a point:

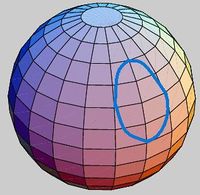
On the ball any cycle is homologous to a point - no tunnels:

Exercise. MRI is a non-intrusive method that allows the use of three-dimensional computer modeling to create images of the internal organs. As a result, doctors are able to determine the state of these organs, for example the integrity of the scull, or blockage of an artery, or the presence of a tumor. Explain why these issues are topological in nature.

More examples of topological issues in computer vision are given below.

Of course, from the practical point of view one has to evaluate these topological features in terms of their significance. For example, is it a big object or small? Is the hole wide or narrow? You can't answer these questions topologically. These are geometrical issues. See Measuring objects.

Exercises

The questions below ask you to evaluate certain topological features. In fact, each question can be answered with an appropriate choice of a homology class. What are the dimensions of those classes?

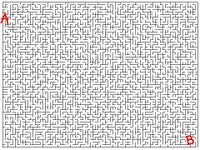
Exercise 1. In the maze, can you get from A to B? Answer