This site is being phased out.
The homology of a gray scale image
We will try to understand the meaning of the homology of gray scale images.
Below is an example of a gray scale image and its "frames", i.e., three thresholded versions. These are binary images that we understand as cell complexes (see Cell decomposition of images). Here white is empty.
For completeness sake one can add a fully white image in the beginning and fully black in the end.
Here is another example:
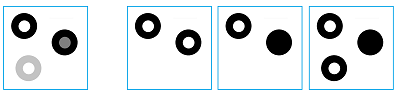
For complete analysis, let's consider this simple image:
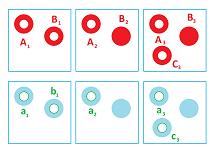
First the image is "thresholded". The lower level sets of the gray scale function of the image form a filtration: a sequence of three binary images, i.e., cell complexes: $K^{1}\hookrightarrow K^{2}\hookrightarrow K^{3},$ where the arrows represent the inclusions. Suppose $A_{i},B_{i},C_{i}$ are the homology classes that represent the components of $K^{i}$ and $a_{i},b_{i},c_{i}$ are the holes, clockwise starting at the upper left corner. The homology groups of these images also form sequences -- one for each dimension $0$ and $1$.
Suppose $F_{1},F_{2}$ are the two homology maps, i.e., homomorphisms of the homology groups generated by the inclusions of the complexes, with $F_{3}=0$ included for convenience. These homomorphisms act on the generators, as follows: \begin{eqnarray*} A_{1} &\rightarrow &A_{2}\rightarrow A_{3}\rightarrow 0,B_{1}\rightarrow B_{2}\rightarrow B_{3}\rightarrow 0, \\ C_{2} &\rightarrow &C_{3}\rightarrow 0,a_{1}\rightarrow a_{2}\rightarrow a_{3}\rightarrow 0, \\ b_{1} &\rightarrow &0,c_{3}\rightarrow 0. \end{eqnarray*}
To avoid double counting, we want to count only the homology classes that don't reappear in the next homology group. As it turns out, a more algebraically convenient way to accomplish this is to count only the homology classes that go to $0$ under these homomorphisms. These classes form the kernels of $F_{1},F_{2},F_{3}$. Now, we choose the homology group of the original, gray scale image to be the direct sum of these kernels: \begin{equation*} H_{0}(\{K^{i}\})=<A_{3},B_{3},C_{3}>,\text{ }H_{1}(\{K^{i}% \})=<b_{1},a_{3},c_{3}>. \end{equation*} Thus the image has three components and three holes, as expected.
As a diagram, the $0$- and $1$-homology groups of the frames and the homomorphisms form two sequences: $$R^2 → R^2 → R^3 → 0,$$ $$R^2 → R^1 → R^2 → 0.$$ Instead of counting objects that do not reappear in the next frame, we use linear algebra to find the cycles in each frame that go to $0$ under $F_{1},F_{2},F_{3}$. These cycles form the kernels $$\ker F_{1}, \ker F_{2}, \ker F_{3}$$ of these linear operators. Then, the homology group of the gray scale image should be $$H_{0}(\{K^{i}\}) = \ker F_{1} \times \ker F_{2} \times \ker F_{3} = 0 \times 0 \times R^3 = R^3,$$ $$H_{1}(\{K^{i}\}) = \ker F_{1} \times \ker F_{2} \times \ker F_{3} = R \times 0 \times R^2 = R^3 .$$ Three components and three holes, again.
This is our conclusion: the homology group of a gray scale image is the product of the kernels of the linear operators generated by the inclusions of its frames.
Exercise: Compute the homology group of the blurred version and the negative of the above image.