This site is being phased out.
The high contrast homology of a gray scale image
Redirect page
Redirect to:
In image analysis one may want to measure the importance of topological features in terms of their contrast.
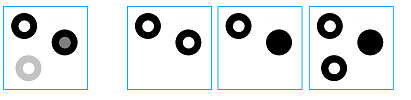
The images below show how the number of objects declines as the contrast threshold increases: $0, 30, 50, 70, 125$:
Recall how we defined the homology group of the image below. First, we created a filtration: a sequence of three binary images: $$K^{1}\hookrightarrow K^{2}\hookrightarrow K^{3},$$ where the arrows represent the inclusions. Suppose $A_{i},B_{i},C_{i}$ are the homology classes that represent the components of $K^{i}$ and $a_{i},b_{i},c_{i}$ are the holes, clockwise starting at the upper left corner.
Also $F_{1},F_{2}$ are the two homology maps, i.e., homomorphisms of the homology groups generated by the inclusions of the complexes, with $F_{3}=0$ included for convenience. These homomorphisms act on the generators, as follows: \begin{eqnarray*} A_{1} &\rightarrow &A_{2}\rightarrow A_{3}\rightarrow 0,B_{1}\rightarrow B_{2}\rightarrow B_{3}\rightarrow 0, \\ C_{2} &\rightarrow &C_{3}\rightarrow 0,a_{1}\rightarrow a_{2}\rightarrow a_{3}\rightarrow 0, \\ b_{1} &\rightarrow &0,c_{3}\rightarrow 0. \end{eqnarray*}
Next, we count only the homology classes that go to $0$ under these homomorphisms. These classes form the kernels of $F_{1},F_{2},F_{3}$. Then, the homology is the direct sum of these kernels: \begin{equation*} H_{0}(\{K^{i}\})=<A_{3},B_{3},C_{3}>,\text{ }H_{1}(\{K^{i}% \})=<b_{1},a_{3},c_{3}>. \end{equation*}
This approach is simple but it has a drawback. From the sequence of homology classes $$a_{1}\rightarrow a_{2}\rightarrow a_{3}\rightarrow0,$$ the one that is chosen to appear in the homology of the image is $a_{3}.$ However this class represents the least prominent feature from the three. This issue becomes more obvious if we take into account all 256 level of gray. For example, for a blurred version of the image we have the sequence of homology classes $$a_{1}\rightarrow a_{2}\rightarrow...\rightarrow a_{255}\rightarrow a_{256}\rightarrow0.$$ Then the last non-zero element will represent the smallest hole with lowest contrast. The better choice to capture the hole would be $a_{1}$ since it represent the largest hole with highest contrast.
Then, alternatively, we define the homology group of the image as \begin{align*} H_{\ast}(\{K^{i}\}) & =H_{\ast}(K^{1})/\operatorname{Im}F_{0}\oplus H_{\ast }(K^{2})/\operatorname{Im}\,F_{1}\oplus H_{\ast}(K^{3})/\operatorname{Im}% \,F_{2}\\ & \simeq H_{\ast}(K^{1})\oplus(\operatorname{Im}\,F_{1})^{\bot}% \oplus(\operatorname{Im}\,F_{2})^{\bot}. \end{align*} Then we still have three components and three holes as $H_{\ast}(\{K^{i}\})$ is generated by the equivalence classes of $A_{1},B_{1},C_{2},a_{1},b_{1},c_{3}.$
Next, one may observe that the contrast of some of the features in the original image is lower than others. These are the holes in the second and the third rings as well as the third ring itself. In the image analysis context one may evaluate the area/volume of the connected components and then classify ones that are too small as noise. The average contrast is another way to evaluate the importance of a component. Yet more measurements are: perimeter, roundness, location, and their combinations.
A different kind of measurement is contrast. By contrast of a lower level set we understand the difference between the highest gray level adjacent to the object and the lowest gray level within the object and the opposite for upper level sets. This measurement is purely topological. Also, unlike the other measurements listed above, contrast is equally applicable to all homology classes not just ones of dimension (or co-dimension) $0$. This fact is reflected in the algebra presented above. Indeed we can compute the contrast as the life-spans (persistence) of these homology classes:
\[% \begin{matrix} {}% p(A_{1})=3, & p(A_{2})=2, & p(A_{3})=1,\\ p(B_{1})=3, & p(B_{2})=2, & p(B_{3})=1,\\ & p(C_{2})=2, & p(C_{3})=1,\\ p(a_{1})=3, & p(a_{2})=2, & p(a_{3})=1,\\ p(b_{1})=1, & & \\ & & p(c_{3})=1.% \end{matrix} \]
Suppose we are only interested in features with high contrast at least $3$ and consider the rest noise. Then the homology classes with persistence of $3$ or higher among the generators are: $A_{1},B_{1},a_{1}.$ However, since the persistence can decrease under algebraic operations, the set of elements of high persistence isn't a subspace of the respective homology group of the filtration. Instead, we look at the noise:
\[% \begin{matrix} {}% 0=\ker F_{3}F_{2}F_{1}, & <A_{2},B_{2},C_{2}>=\ker F_{3}F_{2}, & <A_{3},B_{3},C_{3}>=\ker F_{3},\\ <b_{1}>=\ker F_{3}F_{2}F_{1}, & <a_{2}>=\ker F_{3}F_{2}, & <a_{3},c_{3}>=\ker F_{3}, \end{matrix} \]
Now we "remove" the noise from each of the homology groups of the filtration: \begin{align*} & <A_{1},B_{1}>/0=<A_{1},B_{1}>,<A_{2},B_{2},C_{2}>/<A_{2},B_{2},C_{2}>=0,\\ & <A_{3},B_{3},C_{3}>/<A_{3},B_{3},C_{3}>=0,<a_{1},b_{1}>/<b_{1}>=<a_{1}>,\\ & <a_{2}>/<a_{2}>=0,<a_{3},c_{3}>/<a_{3},c_{3}>=0. \end{align*} Thus the 3-persistent homology of the image is: \begin{align*} H_{0}^{3}(\{K^{i}\}) & =<A_{1},B_{1}>,\\ H_{1}^{3}(\{K^{i}\}) & =<a_{1}>. \end{align*}
To summarize, the homology classes with persistence of $3$ or higher among the generators are: $A_{1},B_{1},a_{1}.$ However, the set of the classes of high persistence isn't a subgroup of the homology group of the respective complex. Instead, we look at the classes with low persistence, i.e., the noise. In particular, the classes in $H_{\ast }(K^{1})$ of persistence 2 or lower form the kernel of $F_{2}F_{1}$. We now "remove" this noise from the homology groups of the filtration by considering their quotients over these kernels. In particular, the $3$-persistent homology groups of the image are: \begin{align*} H_{0}^{3}(\{K^{i}\})& =<A_{1},B_{1}>/0=<A_{1},B_{1}>, \\ H_{1}^{3}(\{K^{i}\})& =<a_{1},b_{1}>/<b_{1}>=<a_{1}>. \end{align*} Observe that the output is identical to the homology of a single complex, i.e., a binary image, with two components and one hole. The way persistence is defined ensures that we can never remove a component as noise but keep a hole in it.
Observe now that the holes in the second and third rings have the same persistence (contrast) and, therefore, occupy the same position in the homology group regardless of their birth dates (gray level). Second, if we shrunk one of these rings, its persistence and, therefore, its place in the homology group wouldn't change. These observations confirm the fact that the homology group of the gray scale image, unlike the barcodes, captures only its topology.
In the case of a Vietoris-Rips complex, not only the barcode, the interval $[birth, death]$, but also the persistence, the number $death - birth$, of a homology class contains information about the size of representatives of these classes. For example, a set of points arranged in a circle will produce a 1-cycle with twice as large birth, death, and persistence than the same set shrunk by a factor of $2$. However, persistence defined as $death/birth$ will have the desired property of scale independence. The same result can be achieved by an appropriate re-parametrizing of the filtration.
Exercise: Compute the persistent homology group of the blurred version and the negative of the above image.