This site is being phased out.
Quotients
Contents
Gluing things together
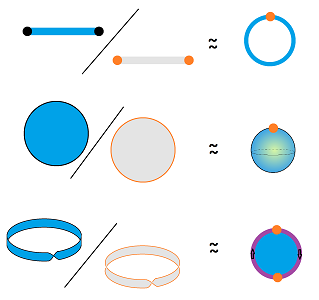
A new way of building new things from old is gluing:
One can build a lot of (topologically) different things with nothing but sheets of paper and a glue-stick:
In light of this gluing metaphor, some of the axioms of equivalence relations will make practical sense. The Reflexivity Axiom, $A \sim A$, can be understood as: every spot of the sheet is glued to itself. The Symmetry Axiom, $A \sim B \Rightarrow B \sim A$, becomes: a drop of glue holds either of the two sheets equally well.
Most of the time, we will attach the sheets edge-to-edge, without overlap. In that case, welding may be a better metaphor:
Then the Transitivity Axiom, $A \sim B, B \sim C \Rightarrow A \sim C$, means: the two seams are fully merged and become indistinguishable.
Thinking of a zipper is also appropriate:
Topologically, zipping a jacket turns a square with two holes into a cylinder with two holes, or, even better, a disk with two holes turns into a disk with three holes:
Making balloon animals is another example:
Meanwhile, we have already seen gluing when we constructed topological spaces from cells as realizations of simplicial complexes:
These realizations, however, were placed within a specific Euclidean space ${\bf R}^N$. We will see that this is unnecessary.
Quotient sets
Before we consider the topological issues, let's take care of the underlying sets.
We pick two examples of somewhat different nature.
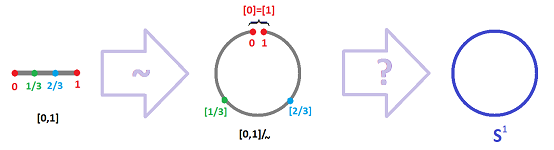
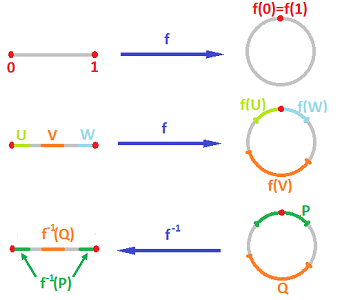
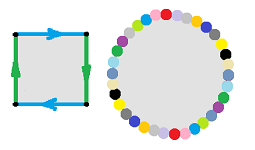
Example (circle). The easiest way to construct the circle ${\bf S}^1$ is to take the closed segment $[0,1]$ and glue the end-points together. The gluing procedure is captured by the following equivalence relation on $X = [0,1]$:
- 1. $0 \sim 1$, and
- 2. $x \sim x$ for all $x\in X$.
The second condition is required by the Reflexivity Axiom and will be assumed implicitly in all examples. Then we record the equivalence relation simply as $$0 \sim 1.$$ Now, notation for the quotient set is: $${\bf S}^1 := [0,1]/_{\sim}.$$ As we know, this is the set of all equivalence classes of this equivalence relation: $$X / _{\sim} := \{[x]: x\in X\},$$ where $$[x]: = \{y\in X: y \sim x\}= \begin{cases} \{0,1\} \text{ if } x=0,1; \\ \{x\} \text{ if } x\in (0,1). \end{cases}$$ The image below is just an illustration of what these equivalence classes look like:
$\square$
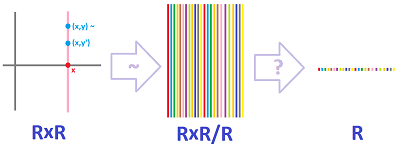
Example (plane). The next example is a familiar one from linear algebra. We let
- $X = {\bf R}^2$ and
- $(x,y) \sim (x,y')$ for all $x,y,y'\in {\bf R}$.
The equivalence classes are the vertical lines. Instead of using the gluing metaphor, we say that each of these lines collapse to a point. Indeed, each of the vertical lines corresponds to its point of intersection with the $x$-axis. Hence, the quotient set corresponds, in this sense, to the real line. Algebraically, we write: $$X/_{\sim} = \{ \{(x,y): y\in {\bf R}\} :\ x\in {\bf R}\} \leadsto \{ x :\ x\in {\bf R}\} = {\bf R}.$$
$\square$
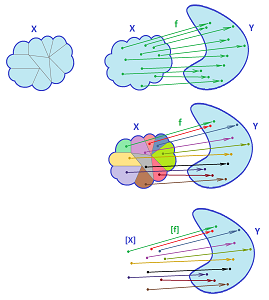
Definition. The function that takes each point to its equivalence class is called the identification function:
- $q: X \to X/_{\sim}$ given by
- $q(x) := [x]$.
It may be called the “gluing” or “attaching” map in a topological context.
When we recognize the quotient as a familiar set, we may try to present the identification map explicitly. In the first example, the identification function $$f: [0,1] \to {\bf S}^1$$ is given by $$f(t) := (\cos(\pi t), \sin(\pi t)),\ t\in [0,1].$$ In the second example, $q$ may be thought of as the projection: $$q: {\bf R}^2 \to {\bf R},$$ given by $$q(x,y) := x,\ x,y\in {\bf R}.$$
Next, we consider a couple of more complex examples of gluing.
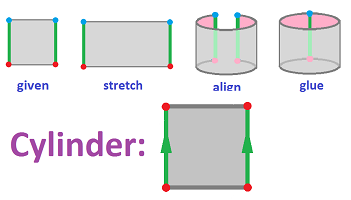
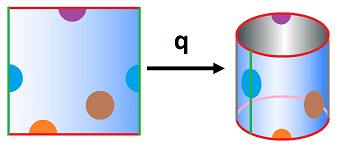
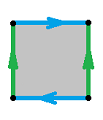
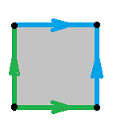
Example (surfaces). One can glue the two opposite edges of the square to create a cylinder:
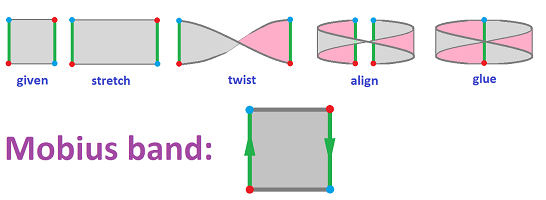
If you twist the edge before gluing, you get the Möbius band:
However, in order to properly interpret this literal gluing in terms of quotients, we need to recognize that, mathematically, only points can be glued to each other. In these two examples, the points are glued pairwise:
Once this is understood, we can sometimes see a pattern of how the points are glued to each other and think of this process as gluing two whole edges, as long as they are oriented properly! These orientations of the edges are shown with arrows that have to be aligned before being glued.
We have here: $$X = [0,1] \times [0,1] = \{(x,y):\ x\in [0,1], y\in [0,1]\}.$$ And the equivalence relation for the cylinder is given by:
- $(x,y) \sim (u,v)$ if $y=v$ and $x,u=0$ or $1$,
or simply:
- $(0,y) \sim (1,y)$.
The equivalence relation for the Möbius band is given by:
- $(x,y) \sim (u,v)$ if $y=1-v$ and $x,u=0$ or $1$,
or simply:
- $(0,y) \sim (1,1-y)$.
$\square$
With all this talk about creating a circle, a torus, etc., we shouldn't fool ourselves into thinking that these are anything more than clues to possible outcomes. Without a topology as a way to capture the proximity, the quotient set will remain a bag of points:
Quotient spaces and maps
Even though we always start with $X$ assumed to be a topological space, the quotient has been, so far, just a set. We can't simply assume that the quotient also has “some” topology without losing the connection to $X$.
What we need is a standard way of imparting or inducing a topology on the quotient set $X/_{\sim}$ from that of $X$. The idea is similar to the way we chose a topology, the relative topology, on a subset of $X$ based on that of $X$. The crucial difference between these two situations is that the functions we use for this purpose point in the opposite directions:
- for a subset, the inclusion $i_A:A\to X$ is a function to $X$, while
- for a quotient set, the identification function $q:X\to X/_{\sim}$ is a function from $X$.
In either case, the issue is that of continuity of the new function.
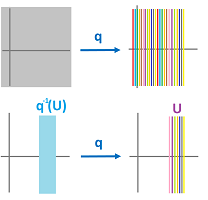
Note that the identification functions in the examples above are familiar. In the second example, $q$ is the projection: $$q : {\bf R}^2 \to {\bf R}$$ given by $$q(x,y) := x.$$ And it is continuous... provided ${\bf R}$ is equipped with the Euclidean topology, of course. Then it's easy to verify that the preimage of an open set is open: $$f^{-1}\left( (a,b) \right) = (a,b) \times {\bf R}.$$
In the first example, the identification function $f$ is the gluing map: $$f : [0,1] \to {\bf S}^1,$$ given by $$f(t) := \left( \cos(\pi t), \sin(\pi t) \right), \ \forall t \in [0,1].$$ Once again, it's continuous provided we supply the circle with an appropriate topology. Naturally, we want the topology of the new topological space to match the relative topology acquired from the inclusion ${\bf S}^1\subset {\bf R}^2$. The standard basis of this topology of the plane consists of disks; therefore, the basis of the topology of the circle should consist of the arcs: $$A(a,b) := \{ \left(\cos(\pi t),\sin(\pi t) \right) :\ t \in (a,b) \},$$ where $(a,b)$ is any interval in ${\bf R}, a<b$.
Clearly, if $0 \leq a,b \leq 1$, then $$f^{-1}\left( A(a,b) \right) = (a,b),$$ which is open. What if $0 < a < 1$ while $1 < b < 2$? Then $$f^{-1}\left( A(a,b) \right) = (a,1] \cup [0,b).$$ It is also open relative to $[0,1]$. Again, we have a continuous function.
Definition. Given a topological space $X$ and an equivalence relation $\sim$ on $X$, the quotient space $X/ \sim$ is a topological space on the quotient set $X/ _{\sim}$ such that $U$ is open in $X/ _{\sim}$ iff $q^{-1}(U)$ is open in $X$, where $q$ is the identification function.
To put this differently, if $\tau$ is the topology of $X$ then $$\{ q^{-1}(U) :\ U \in \tau \}$$ is the topology of $X/ _{\sim}$.
Exercise. Prove that this collection of sets is indeed a topology.
Exercise. What if we replace “topology” with “a basis of neighborhoods”?
Since the identification function is now continuous, we may call it the identification map.
In the example of the circle above, the preimage of an arc is either an open interval or the union of two half-open intervals at the end-points. Let's consider the second example from the last subsection.
Example (plane). The equivalence classes are the vertical lines and, therefore, the preimage of any subset $U \subset X/_{\sim}$ is made of vertical lines. This set is an open vertical band when the lines in $U$ cut an open interval on the $x$-axis:
Therefore, the topology on the quotient set is that of ${\bf R}$.
$\square$
Exercise. Consider the two equivalence relations for ${\bf R}^2$ below: $(x,y)\sim (a,b)$ if
- (a) $x^2+y=a^2+b$, and
- (b) $x^2+y^2=a^2+b^2$.
Identify these quotient spaces ${\bf R}^2 / _{\sim}$ as familiar topological spaces.
As we have seen, the quotient construction may add non-trivial homology classes. It's true for all dimensions except $0$:
Theorem. If $X$ is path-connected then so is $X/_{\sim}$, for any equivalence relation $\sim$.
Proof. Since the identification function $q : X \to X/_{\sim}$ is both continuous and onto, the new space $X/_{\sim} = \operatorname{Im} q$ is path-connected as the image of a path-connected topological space. $\blacksquare$
Theorem. If $X$ is compact then so is $X/_{\sim}$, for any equivalence relation $\sim$.
Exercise. Prove the theorem.
We discover then that, instead of thinking in terms of the topological space of equivalence classes, it may be more convenient to consider a familiar topological space as a candidate and then prove that they are homeomorphic. In fact,
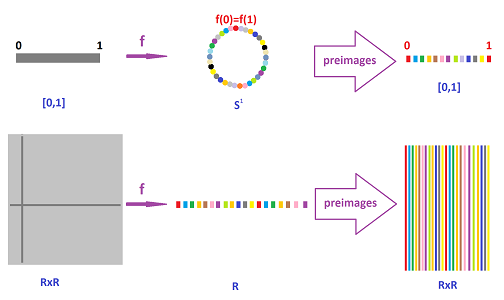
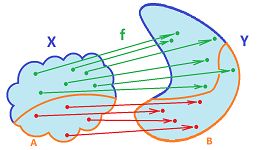
We just need to find an appropriate target space for this function. Indeed, suppose $f:X\to Y$ is an onto function from a topological space $X$ to a set $Y$. Then we define $$a \sim b \Leftrightarrow a,b\in f^{-1}(y),y\in Y,$$ or $$a \sim b \Leftrightarrow f(a)=f(b).$$ This is an equivalence relation on $X$ and its equivalence classes are the preimages of points under $f$. Then the topology on $Y$ is created by the definition from the last subsection.
For the two examples of maps from the last subsection, $$f:[0,1]\to {\bf S}^1$$ and $$f:{\bf R} \times {\bf R} \to {\bf R},$$ the idea is illustrated below:
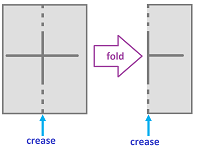
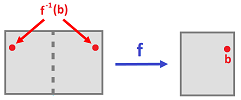
Example (folding). Consider first folding the $xy$-plane, $$f(x,y) := (|x|,y).$$
Now, the folding of the rectangle $[-1,1] \times [0,1]$ is given by the same formula and is continuous as a restriction of $f$.
$\square$
Not every continuous function, however, is an identification map. The following theorem presents the necessary extra conditions.
Theorem. Let $f:X\to Y$ be an onto map. If
- $f$ maps open sets of $X$ to open sets in $Y$, or
- $f$ maps closed sets of $X$ to closed sets in $Y$,
then $f$ is an identification map.
Exercise. Prove the theorem.
Exercise. Given an identification map $f:X\to Y$ and a subset $A\subset X$, show that the restriction $f\Big|_A:A\to f(A)$ doesn't have to be an identification map.
Theorem. Let $q:X\to X/_{\sim}$ be the identification map. Suppose $Y$ is a topological space and $f:X\to Y$ is a map that is constant on each equivalence class of $X$. Then there is a map $f':X/_{\sim}\to Y$ such that $f'q=f$. In other words, there is a map for the bottom arrow to make this diagram commutative: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{cccccccccc} X & & \\ \da{q} & \searrow ^f & \\ X/_{\sim} & \ra{f'} & Y \end{array} $$
Exercise. Prove the theorem.
What happens to maps when one or both of the spaces are subjected to the quotient construction?
Suppose first that just the domain of a map $f:X\to Y$, is equipped with an equivalence relation. Then quotient map $[f]:X/_{\sim} \to Y$ of $f$ is given by $[f]([x]):=f(x)$.
Of course, the new map is well-defined only if $f$ takes each equivalence class to a single point, i.e., $$x\sim x' \Rightarrow f(x)=f(x').$$
Proposition. The quotient map of $fX\to Y$, when defined, is continuous.
Exercise. Prove the proposition.
Exercise. What of the target space $Y$ has an equivalence relation. Analyze the possibility of $[f]:X \to Y/_{\sim}$.
The general case of a map from a quotient space to a quotient space is familiar from algebra. Given a map $f:X\to Y$, its quotient map $[f]:X/_{\sim} \to Y/_{\sim}$ is given by $$[f]([x]):=[f(x)].$$
Exercise. (a) When is $[f]$ well-defined? (b) Prove it is continuous.
Examples
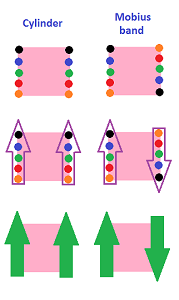
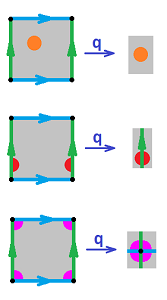
Example (cylinder). Let's consider the cylinder construction and examine what happens to the topology. The results are similar to the example of the circle: the preimage of an open disk under the identification map is either an open disk or the union of two half-disks at the edge.
$\square$
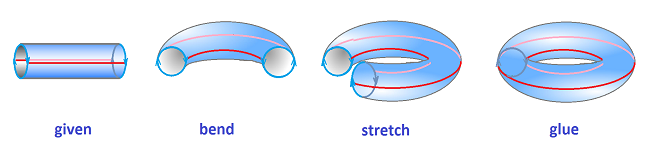
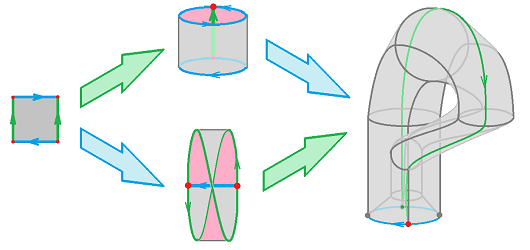
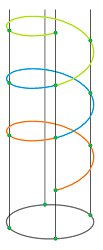
Example (torus). One can get the torus ${\bf T}^2$ from the cylinder by gluing the top to the bottom: $$(x,0) \sim (x,1).$$ This is how it is visualized:
The equivalence relation for the torus built directly from the square is as follows: $$(0,y) \sim (1,y)\text{ and } (x,0) \sim (x,1).$$ This way the torus is still a quotient of the square. Then one can easily see the three types of neighborhoods:
There is an alternative way to glue (in the real world) the edge to itself:
Since the outcome is supposed to be the same, we discover a self-homeomorphism of the torus which is non-trivial in the sense that a longitude is mapped to a latitude. Such a homeomorphism would, in a sense, turn the torus inside out.
$\square$
Note: solutions of a “doubly periodic” differential equation, $(x',y')=f(x,y)$ with $f(x+T,y)=f(x,y+S)=f(x,y)$, can be thought of as paths on the torus.
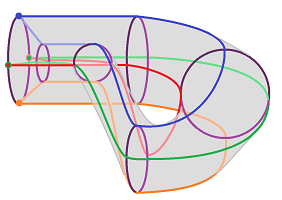
Example (Klein bottle). One can get the Klein bottle ${\bf K}^2$ from the cylinder by gluing the top to the bottom in reverse: $$(x,0) \sim (1-x,1).$$ The horizontal arrows point in the opposite directions:
and, to align them, we need to “cut” through the cylinder's side. This is how it is visualized:
To understand that there is really no self-intersection, one can think of the Klein bottle as a circle moving through space. For example, consider a smoke ring that leaves your mouth, floats forward, turns around, shrinks, and then floats back in:
$\square$
Just as with the torus, there are two ways to construct the Klein bottle from the square:
Exercise. Identify this space:
Example (projective plane). We can also make the projective plane ${\bf P}^2$ from this square:
One can understand it as if the diametrically opposite, or “antipodal”, points on the boundary of the disk are identified. Alternatively, we start with ${\bf R}^2 \setminus \{ 0,0 \}$ and choose the lines through the origin to be the equivalence classes.
$\square$
Example (complex projective plane). It is similar, but the reals replaced with the complex numbers: $${\bf CP}^n:={\bf S}^{2n+1} / _{\sim},$$ where $$z\sim z' \Leftrightarrow z=e^{i\theta}z',\ \exists\theta.$$ and $${\bf S}^{2n+1}=\{z\in {\bf C}^{n+1}:\ ||z||^2=1\}.$$
$\square$
Exercise. The projective plane ${\bf P}^2$ contains the Mobius band ${\bf M}^2$. Find it.
Exercise. What happens if we identify the antipodal points on the circle?
Example. There are many ways to create a circle. An insightful way is to make it from the line. One just winds the helix, which is ${\bf R}$ topologically, around the circle, ${\bf S}^1$:
Then the identification map $f : {\bf R} \to {\bf S}^1$ may be thought of as the restriction of the projection of the $3$-space to the plane, or it is given explicitly by: $$f(t) := (\cos(\pi t), \sin(\pi t)),\ t \in {\bf R}.$$ $\square$
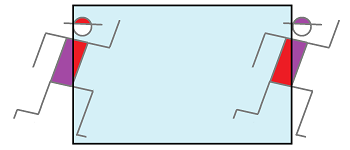
Example. Suppose we have a room with two doors and suppose as you exit through one door you enter through the other (it's the same door!). If you look through this door, this is what you see:
The reason is that, in this universe, light travels in circles... If you run fast enough, an outside observer might see (parts of) you at two different places at the same time:
To produce this effect, we identify the front wall with the back wall.
$\square$
Exercise. Describe this situation as a quotient of the cube.
Exercise. What if, as you exit one door, you enter the other -- but upside down? Which of the two below is the correct view?
Exercise. What if the front wall is turned $90$ degrees before it is attached to the back wall? Sketch what you'd see.
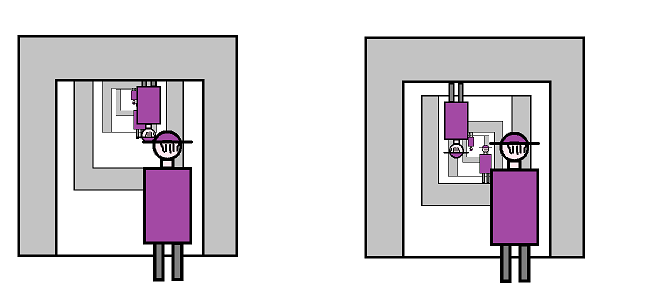
Exercise. If you've seen two mirrors hung on the opposite walls of the room, you know what they show: you see your face as well as the back of your head, with this pattern repeated indefinitely. How can we achieve this effect without mirrors? Using quotients, construct a topological space with this effect as (a) an enfilade of rooms, separated by glass, with a person in each; (b) a compact space.
Exercise. Repeat the last exercise for the second, web-cam, image above.
Exercise. What if the room had $n$ walls? What if we have mirrors on all four walls of the room? Five walls, $n$ walls? Four walls, ceiling, and floor?
Exercise. Interpret the Pasting Lemma about the continuity of a piece-wise defined function $f:X\to Y$ $$f(x)= \begin{cases}{} f_A(x) & \text{ if } x\in A, \\ f_B(x) & \text{ if } x\in B, \end{cases} $$ in terms of the quotient construction.
Exercise. Suppose our sphere ${\bf S}^2$ is the unit sphere in ${\bf R}^3$. Define a map $f:{\bf S}^2 \to {\bf R}^4$ by $f(x,y,z):=(x^2-y^2,xy,xz,yz)$. Use $f$ to construct an embedding of the projective plane ${\bf P}^2$ to ${\bf R}^4$.
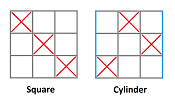
Exercise. Explore the winning combinations and the strategies for playing tic-tac-toe on the main surfaces:
Link to the file: tic.xls
Exercise. Which space do we obtain if we collapse the boundary of the Mobius band to a point? Hint: the boundary is a circle.
Exercise. Describe the space resulting from the ring if we identify antipodal pairs of points on the outer circle and also identify the antipodal pairs of points on the inner circle.
Collapsing subsets and pairs of spaces
The idea of “removing” something by means of the quotient construction is well-known in algebra and, in fact, we have used it to introduce homology. Now, we shall see that the idea is also applicable in topology.
The idea is to simply collapse the subset to be removed to a point. Then, there is only one non-trivial equivalence class!
Notation. Since we use the same notation as in algebra, the difference in the meaning needs to be emphasized:
- in algebra: $X / A$ is given by the equivalence relation: $x \sim y$ iff $x-y\in A$;
- in topology: $X / A$ is given by the equivalence relation: $x \sim y$ iff $x,y\in A$.
Exercise. The above example of projecting the plane onto the $x$-axis can be understood algebraically as the plane modulo the $y$-axis. Sketch this quotient if understood topologically.
With this simple equivalence relation, we can build a lot.
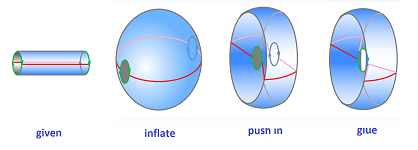
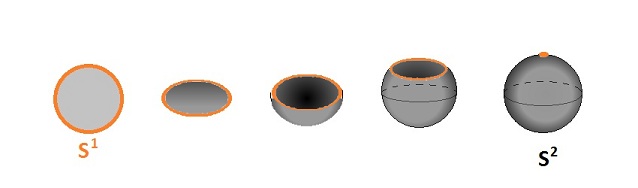
For example, the circle is still made from the segment: $$[0,1]/_{\sim}= [0,1] / \{0,1\} ={\bf I} / \partial {\bf I} \approx {\bf S}^1 .$$ The sphere is made from the disk: $${\bf B}^2/{\bf S}^1 \approx {\bf S}^2 ,$$ as illustrated below:
Exercise. Prove that the latter is a homeomorphism. Hint: use the stereographic projection.
More generally, one can construct the $n$-sphere from the $n$-ball by collapsing its boundary to a point: $${\bf S}^n = {\bf B}^n/{\bf S}^{n-1} .$$ Note that the $n$-sphere is constructed topologically, not as a subset of ${\bf R}^{n+1}$.
Definition. Given $X$ and a subset $A$, the equivalence relation defined by: $$x \sim y,\ \forall x,y \in A,$$ produces a quotient space denoted by: $$X/A.$$ It is read “$X$ modulo $A$”.
Once again, we need to keep in mind that this is just a special kind of a quotient space. The equivalence classes are
- $\{x\}$ for $x\in X \setminus A$, and
- $A$.
A few simple examples below:
Exercise. Sketch the torus with a longitude, and then a latitude, collapsed.
Exercise. What is ${\bf R}^2 / {\bf Z}^2$?
One can use this idea to develop topology of pairs $(X,A)$, where $X$ is a topological space and $A$ is its subset.
Notation. The topology of the pair is that of $X$ with $A$ collapsed: $$(X,A):=X/A,$$ and, further, its homology is: $$H(X,A):=H(X/A).$$
We can interpret all the previous development in light of this new approach by assuming that $$X=(X,\emptyset).$$
The main advantage of this approach is the ease of dealing with maps. Suppose there is a map between two spaces $$f:X\to Y,$$ both of which are supplied with equivalence relations. Recall that one can construct the quotient map $[f]$ of $f$ as a map of quotients $$[f]:X/_{\sim} \to Y/_{\sim}$$ by setting $$[f]([a]):=[f(a)].$$ However, it is possible only if each equivalence class on $X$ is mapped into an equivalence class on $Y$: $$f([a]) \subset [f(a)].$$ In other words, we have to require that $$a\sim b \Rightarrow f(a)\sim f(b).$$ Now, when these two equivalence relations are simply collapses, $X/A$ and $Y/B$, this requirement becomes much simpler: $$a\in A \Rightarrow f(a)\in B,$$ or $$f(A)\subset B.$$ Another way to put it is that the restriction of $f$ to $A$ with target space $B$ $$f\Big|_A:A \to B$$ has to be well-defined. In other words, this diagram is commutative: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{cccccccccc} A & \ra{f|_A} & B \\ \quad\da{i_A} & \searrow & \quad\da{i_B} \\ X & \ra{f} & Y, \end{array} $$ where $i_A,i_B$ are the inclusions.
Our interpretation is that $f$ is now a map of pairs: $$f:(X,A)\to (Y,B).$$
Exercise. Prove that the composition of two maps of pairs is also a map of pairs. Is this a category? Define the chain maps and the homology maps of maps of pairs.
Definition. The one-point union of two spaces $X,Y$ is defined by $$X \vee Y := \left( X \sqcup Y \right) / { \{x_0, y_0\} },$$ for some $x_0\in X,y_0 \in Y$.
Exercise. Under what circumstances is the one-point union independent of the choice of the points?
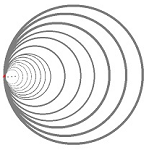
Example (Hawaiian earring). The Hawaiian earring is the subset of the plane that consists of infinitely many circles with just one point in common:
Specifically,
$\square$
Exercise. Show that the Hawaiian earring $X$ is path-connected.
Exercise. Let $Y={\bf R} / {\bf Z}$ be the quotient of the real line with all integer points identified. It can be understood as an “infinite bouquet of circles”. Show that the Hawaiian earring $X$ is not homeomorphic to $Y$.
Exercise. Explain the topology of ${\bf R} / {\bf Q}$.