This site is being phased out.
Maps of graphs
Contents
Continuous functions and discrete functions
Any study of topology would be incomplete without considering continuous transformations of objects, also known as maps.
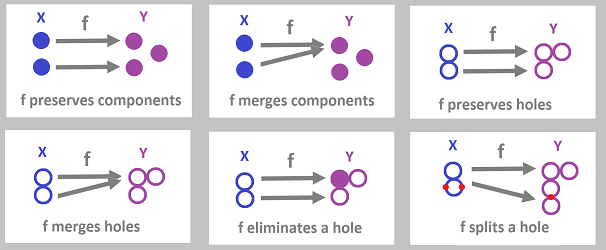
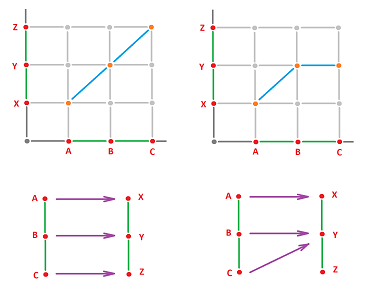
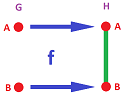
Below, we sketch a few simple examples of maps. One should notice that simply comparing the number of topological features, i.e., components and holes, in the domain and the target spaces doesn't reveal the complete picture. Instead, we want to track each of these features and record what map does to it.
Exercise. We “split” the hole here, why don't we split a component?
In order to be able to employ the algebraic machinery we've started to develop, we would like to match these transformations with their discrete counterparts, as functions of graphs: $$f:G\to J,$$ and then make sure that these functions reproduce these “topological events”.
To sort this out, we start with just the nodes.
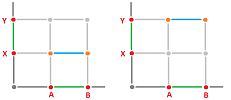
Example. To capture the behavior of the maps above that preserve and merge components, we consider two edge-less graphs $G$ and $J$: $$N_G=\{A,B\},\ E_G=\emptyset,\ N_J=\{X,Y,Z\},\ E_J=\emptyset,$$ and define a “function of nodes”: $$f_N:N_G \to N_J$$ by either
- $f_N(A)=X,\ f_N(B)=Y$, or
- $f_N(A)=X,\ f_N(B)=X$.
Then, of course, these functions generate point-by-point functions on the realizations of these graphs and those functions demonstrate the topological behavior depicted above.
$\square$
Next, we need to understand what may happen to an edge under such a “discrete” function.
It is natural to initially assume that the edges should be taken to edges, by means of a certain function: $$f_E:E_G \to E_J.$$ Such an assumption doesn't seem to cause any problems; in fact, it matches our basic interpretation of graphs as combinations of “agents” and the relations between them. Indeed, we map an agent to an agent and a relation to a relation.
However, what about a constant function? What is the discrete counterpart of the function $$f:X\to Y,\ f(x)=y_0,\ \forall x\in X?$$ An easy answer is to allow an edge to be taken to a node, the event that we will call a “collapse”: $$AB\in E_G,\ f(AB)=X \in N_J.$$
So, we have learned that a function $f:G\to J$ between graphs should be a combination of two, the node function: $$f_N:N_G \to N_J.$$ and the edge function: $$f_E:E_G \to E_J \cup N_J.$$
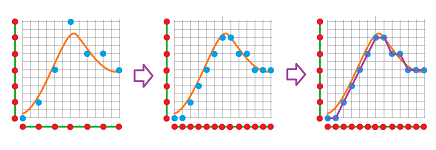
Finding a specific discrete representation, or a counterpart, of a given continuous transformation may require approximation and even refining the graph:
This issue is discussed at a later time and for now we will be satisfied with an analogy.
Graph maps
We still don't have a valid discrete counterpart of a continuous function.
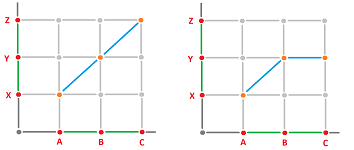
Example. Consider two single-edge graphs: $$N_G=\{A,B\},\ E_G=\{AB\},\ N_J=\{X,Y\},\ E_J=\{XY\}.$$ What functions can we define between them?
Let's we assume that $$f_E(AB)=XY.$$ Then we can have several possible values for $A,B$:
- 1. $f_N(A)=X, \ f_N(B)=Y$,
- 2. $f_N(A)=Y, \ f_N(B)=X$,
- 3. $f_N(A)=X, \ f_N(B)=X$,
- 4. $f_N(A)=Y, \ f_N(B)=Y$.
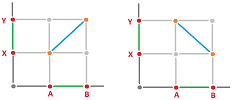
The first two options make sense because they preserve the relation between the agents. This is not the case for options 3 and 4! By looking at the graphs of these functions (on graphs), we realize that what we accept here is continuity:
and what we reject is the discontinuity:
$\square$
Example. Let's start over with the assumption:
- $f_N(A)=X, f_N(B)=X$.
The only way to make sense of these is to define the value of the edge to be a node:
- $f_E(AB)=X$.
And for
- $f_N(A)=Y, f_N(B)=Y$,
we set
- $f_E(AB)=Y$.
Then, we simply have two constant functions here.
$\square$
What we have learned is that the values of the function on the nodes dictate the values on the edges, and vice versa.
Keeping in mind that we are after a discrete analogue of continuous functions, let's consider another example.
Example. Given two two-edge graphs: $$N_G=\{A,B,C\},\ E_G=\{AB,BC\},\ N_J=\{X,Y,Z\},\ E_J=\{XY,YZ\}.$$ What functions can we define between them?
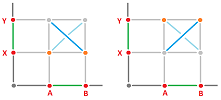
Consider just these three possibilities:
They are given by these functions:
- (1) $f_N(A)=X, \ f_N(B)=Y, \ f_N(C)=Z, \ f_E(AB)=XY, \ f_E(BC)=YZ$,
- (2) $f_N(A)=X, \ f_N(B)=Y, \ f_N(C)=Y, \ f_E(AB)=XY, \ f_E(BC)=Y$,
- (3) $f_N(A)=X, \ f_N(B)=Y, \ f_N(C)=Z, \ f_E(AB)=XY, \ f_E(BC)=Z$.
$\square$
Even a casual look at the graphs reveals the difference, which is the presence or absence of continuity. Indeed, these three graphs look like they could have come from a calculus textbook as illustrations of the issue of continuity vs discontinuity, at a point $x=B$, of a piece-wise defined function: $$\lim _{x\to B-} f(x) =f(B) =\lim _{x\to B+} f(x).$$
We need to ensure this kind of continuity. We plot the nodes first and then attach the edges to them. If this impossible, the function can't be continuous and should be discarded.
We require from the edge function $f_E$ the following:
- for each edge $e$, $f_E$ takes its end-points to the end-points of $f_E(e)$.
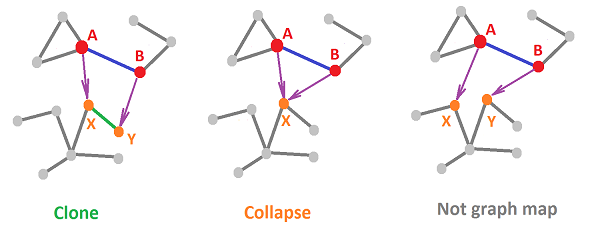
Or, in a more compact form, $$f_N(A)=X, \ f_N(B)=Y \Leftrightarrow f_E(AB)=XY.$$ We say that, in this case, the edge is cloned.
But what about the collapsed edges? It's easy; we just require:
- for each edge $e$, if $e$ is taken to node $X$, then so are its end-points, and vice versa.
Or, in a more compact form, $$f_N(A)=f_N(B)=X \Leftrightarrow f_E(AB)=X .$$
Definition. A function of graphs $f:G\to J$, $$f=\{ f_N:N_G\to N_J,f_E:E_G \to E_J \cup N_J \},$$ is called a graph map if $$f_E(AB)= \begin{cases} f_N(A)f_N(B) & \text{ if } f_N(A) \ne f_N(B),\\ f_N(A) & \text{ if } f_N(A) = f_N(B). \end{cases}$$
In the most abbreviated form, the discrete continuity condition is: $$f(AB)=f(A)f(B),$$ with the understanding that $XX=X$.
With this property assumed, we only need to provide $f_N$, and $f_E$ will be derived.
This idea also allows us to realize graph maps as continuous functions.
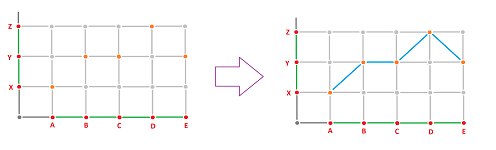
Example. Suppose $f:G\to J$ is such a map and suppose the two graphs are realized: $$|G|=[A,E] \subset {\bf R},\ |J|=[X,Z] \subset {\bf R}.$$ We are looking then for a continuous function $$|f|:[A,E]\to [X,Z].$$
We will need the node function $f_N$ only. Suppose $$f_N(A)=X, \ f_N(B)=Y, \ f_N(C)=Y, \ f_N(D)=Z, \ f_N(E)=Y.$$ Then, of course, we set $$|f|(A)=X, \ |f|(B)=Y, \ |f|(C)=Y, \ |f|(D)=Z, \ |f|(E)=Y.$$
Now we can see how easy it is to reconstruct the rest of the function. We just need to connect these points and, even though all we need is continuity, we simply connect them by straight segments. The formulas are familiar: $$|f|(tA+(1-t)B)=tX+(1-t)Y, \ t\in [0,1].$$ It's a bit trickier for the next edge: $$|f|(tB+(1-t)C)=tY+(1-t)Y=Y, \ t\in [0,1],$$ but it still works! We can handle collapses too.
$\square$
Exercise. Prove the continuity of $|f|$.
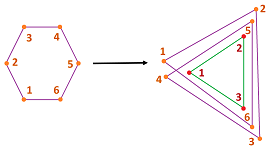
Below we illustrate these ideas for general graphs. Here are two "continuous" possibilities for a discrete function and one "discontinuous":
Exercise. Prove that the composition of two graph maps is a graph map.
Exercise. Under what circumstances is there the inverse of a graph map which is also a graph map?
Chain maps
We can now move on to algebra.
Example. We consider the maps of the two two-edge graphs given above: $$\begin{array}{lll} N_G=\{A,B,C\},& E_G=\{AB,BC\},\\ N_J=\{X,Y,Z\},& E_J=\{XY,YZ\}; \end{array}$$ and the two graph maps.
The key idea is to think of graph maps as functions on the generators of the chain groups: $$C_0(G)=< A,B,C >,\ C_1(G)=< AB,BC >,$$ $$C_0(J)=< X,Y,Z >,\ C_1(J)=< XY,YZ >.$$ Let's express the values of the generators in $G$ under $f$ in terms of the generators in $J$.
The first function is given by: $$\begin{array}{lllll} &f_N(A)=X,&f_N(B)=Y,&f_N(C)=Z,\\ &f_E(AB)=XY,&f_E(BC)=YZ.& \end{array}$$ It is then written coordinate-wise as follows: $$\begin{array}{lllll} &f_0([1,0,0]^T)=[1,0,0]^T,&f_0([0,1,0]^T)=[0,1,0]^T,&f_0([0,0,1]^T)=[0,0,1]^T,\\ &f_1([1,0]^T)=[1,0]^T,&f_1([0,1]^T)=[0,1]^T. \end{array}$$ The second is given by: $$\begin{array}{lllll} &f_N(A)=X, &f_N(B)=Y,&f_N(C)=Y,\\ &f_E(AB)=XY,&f_E(BC)=Y. \end{array}$$ It is written coordinate-wise as follows: $$\begin{array}{lllll} &f_0([1,0,0]^T)=[1,0,0]^T, &f_0([0,1,0]^T)=[0,1,0]^T, &f_0([0,0,1]^T)=[0,0,1]^T,\\ &f_1([1,0]^T)=[1,0]^T, &f_1([0,1]^T)=0. \end{array}$$ The very last item requires special attention: the collapsing of an edge in $G$ does not produce a corresponding edge in $J$. This is why we make an algebraic decision to assign it the zero value.
As always, it suffices to know the values of a function on the generators to recover the whole homomorphism. These two functions $f_N$ and $f_E$ generate two homomorphisms: $$f_0:C_0(G) \to C_0(J),\ f_1:C_1(G) \to C_1(J).$$ It follows that the first homomorphism is the identity and the second can be thought of as a projection.
$\square$
Exercise. Prove the last statement.
Exercise. Find the matrices of $f_0,f_1$ in the last example.
Exercise. Find the matrices of $f_0,f_1$ for $f:G\to J$ given by $f_E(AB)=XY, \ f_E(BC)=XY$.
Let's take another look at the “discrete continuity conditions” from the last subsection. No matter how compact these conditions are, one has to explain that the collapsed case appears to be an exception to the general case. To get around this inconvenience, let's find out what happens under $f$ to the boundary operator of the graph.
Example. We have two here: $$\begin{array}{lll} \partial _G: &C_1(G) \to C_0(G)\\ \partial _J: &C_1(J) \to C_0(J), \end{array}$$ one for each graph.
Now, we just use the fact that $$\partial (AB) = A + B,$$ and the continuity condition takes this form: $$\partial (f_1(AB))=f_0( \partial (AB)).$$ It applies, without change, to the case of a collapsed edge! Indeed, if $AB$ collapses to $X$, both sides are $0$: $$\begin{array}{lllll} \partial (f_1(AB)) &=\partial (0) &=0;\\ f_0( \partial (AB))&= f_0( A+B)=f_0(A)+f_0(B)=X+X &=0. \end{array}$$
$\square$
We follow this idea and introduce this concept.
Definition. The chain map generated by a graph map $f:G \to J$ is a pair of homomorphisms $f_{\Delta}:=\{f_0,f_1\}$: $$f_0:C_0(G) \to C_0(J),$$ $$f_1:C_1(G) \to C_1(J),$$ generated by $f_N$ and $f_E$ respectively.
By design, these two homomorphisms satisfy the following.
Theorem (Algebraic Continuity). For any graph map $f:G \to J$, its chain map satisfies: $$\partial _Jf_1(e)=f_0( \partial _G e),$$ for any edge $e$ in $G$.
Whenever the boundary operator can be properly defined, we can use this condition in any dimension and not just for graphs.
Exercise. Suppose a graph map collapses all edges. Find its chain map.
Exercise. Find the matrix of the chain map of a graph map that shifts by one edge a graph of $n$ edges arranged in (a) a string, (b) a circle.
Exercise. Find the matrix of the chain map of a graph map that folds in half a graph of $2n$ edges arranged in (a) a string, (b) a circle, (c) a figure eight; also (d) for a figure eight with $4n$ edges -- the other fold.
Exercise. Find the matrix of the chain map of a graph map that flips a graph of $2n$ edges arranged in (a) a string, (b) a circle, (c) a figure eight; also (d) for a figure eight with $4n$ edges -- the other flip.
Theorem. Transitioning to chain maps preserves the identity: $$(\operatorname{Id}_G)_0={\rm Id}_{C_0(G)},\ ({\rm Id}_G)_1={\rm Id}_{C_1(G)}.$$
Theorem. Transitioning to chain maps preserves the compositions: $$(fg)_{0}=f_{0}g_{0},\ (fg)_{1}=f_{1}g_{1}.$$
Theorem. Transitioning to chain maps preserves the inverses: $$(f^{-1})_{0}=f_{0}^{-1},\ (f^{-1})_{1}=f_{1}^{-1}.$$
Exercise. Prove these three theorems.
A wonderfully compact form of the above condition is below: $$\begin{array}{|c|} \hline \quad \partial f=f \partial \quad \\ \hline \end{array} $$ We will see this identity a lot later. An appropriate way to describe this is to say that the chain maps and the boundary operators commute. The idea is visualized with a “commutative diagram”.
Commutative diagrams
This very fruitful approach is used throughout.
Compositions of functions can be illustrated as flowcharts:
In general, we represent a function $f : X \to Y$ diagrammatically as a black box that processes the input and produces the output: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccccccc} \text{input} & & \text{function} & & \text{output} \\ x & \ra{} & \begin{array}{|c|}\hline\quad f \quad \\ \hline\end{array} & \ra{} & y \end{array} $$ or, simply, $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} X & \ra{f} & Y \end{array} $$ Now, what if we have another function $g : Y \to Z$; how do we represent their composition $fg=g \circ f$?
To compute it, we “wire” their diagrams together consecutively: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccccccc} x & \ra{} & \begin{array}{|c|}\hline\quad f \quad \\ \hline\end{array} & \ra{} & y & \ra{} & \begin{array}{|c|}\hline\quad g \quad \\ \hline\end{array} & \ra{} & z \end{array}$$ The standard notation is the following: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} X & \ra{f} & Y & \ra{g} & Z \\ \end{array} $$ Or, alternatively, we might emphasize the resulting composition: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} & X & \ra{f} & Y \\ & _{gf} & \searrow & \da{g} \\ & & & Z \end{array} $$ We say the new function “completes the diagram”.
The point illustrated by the diagram is that, starting with $x\in X$, you can
- go right then down, or
- go diagonally;
and either way, you get the same result: $$g(f(x))=(gf)(x).$$
Specifically, this is how the values of the functions are related: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} & x \in X & \ra{f} & Y \ni f(x) \\ & _{gf} & \searrow & \da{g} \\ & (gf)(x) & \in & Z \ni g(f(x)) \end{array} $$
Example. As an example, we can use this idea to represent the inverse function $f^{-1}$ of $f$. It is the function what completes the diagram with the identity function on $X$: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} & X & \ra{f} & Y \\ & _{{\rm Id}_X} & \searrow & \da{f^{-1}} \\ & & & X \end{array} $$ The restriction of $f:X\to Y$ to subset $A\subset X$ completes this diagram with the inclusion of $A$ into $X$: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} & A & \hookrightarrow & X \\ & _{f|_A} & \searrow & \da{f} \\ & & & Y \end{array} $$
$\square$
Diagrams like these are used to represent compositions of all kinds of functions: continuous functions, graph functions, homomorphisms, linear operators, and many more.
Exercise. Complete the diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{cccccc} \ker f & \hookrightarrow & X \\ & _{?} \searrow & \da{f}\\ & & Y& \end{array} $$
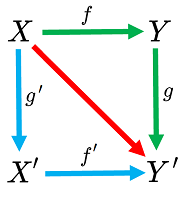
The diagram may be a square, or any other shape: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{cccccccccc} X & \ra{f} & Y \\ \da{g'} & \searrow & \da{g} \\ X' & \ra{f'} & Y' \end{array} $$
Again, go right then down, or go down then right, with the same result: $$gf = f'g'.$$ Both give you the diagonal function!
This identity is the reason why it makes sense to call such a diagram “commutative”. To put it differently,
The image above explains how the blue and green threads are tied together in the beginning -- as we start with the same $x$ in the left upper corner -- and at the end -- where the output of these compositions in the right bottom corner turns out to be the same. It is as if the commutativity turns this combination of loose threads into a piece of fabric!
The algebraic continuity condition in the last subsection $$\partial _Jf_1(e)=f_0( \partial _G e)$$ is also represented as a commutative diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{cccccccccc} C_1(G) & \ra{f_1} & C_1(J) \\ \da{\partial _G} & \searrow & \da{\partial _J} \\ C_0(G) & \ra{f_0} & C_0(J). \end{array} $$
Exercise. Draw a commutative diagram for the composition of two chain maps.
Exercise. Restate in terms of commutative diagrams the last two theorems in the last subsection.
Cycles and boundaries under chain maps
Ultimately, our interest is to track the topological changes as one graph is mapped to another. Given a graph map $f:G\to J$, the main two questions are about the two topological features we have been studying:
- 1. What is the counterpart in $J$ of each component of $G$ under $f$?
- 2. What is the counterpart in $J$ of each hole of $G$ under $f$?
However, these questions are imprecise.
As we know, the topological features are fully captured by the homology groups of these graphs and we can rephrase these questions as:
- 1. How does $f$ transform the $0$th homology group $H_0(G)$ (components) of $G$ into the $0$th homology group $H_0(J)$ of $J$?
- 2. How does $f$ transform the $1$st homology group $H_1(G)$ (cycles) of $G$ into the $1$st homology group $H_1(J)$ of $J$?
To answer these questions we need to conduct a further algebraic analysis of $f$.
Let's review. First, $f$ is a pair of functions:
- 1. $f_N:N_G\to N_J$, and
- 2. $f_E:E_G\to E_J \cup N_J$.
These two generate the chain map $f_{\Delta}$ of $f$, which is a pair of homomorphisms:
- 1. $f_0:C_0(G)\to C_0(J)$, and
- 2. $f_1:C_1(G)\to C_1(J)$.
These two commute with the boundary operator: $$f_0\partial=\partial f_1 .$$
These homomorphisms reveal what happens to the cycles. First, we have no interest in the $1$-chains that aren't $1$-cycles. That's why we consider the restriction of $f_1$ to the group of cycles $Z_1(G)$: $$f_1\Big|_{Z_1(G)}:Z_1(G)\to C_1(J);$$ it has the same values as the original. Now a crucial step.
Theorem. $f_1$ takes cycles to cycles.
Proof. Suppose $\partial _G(x)=0$, then by the commutativity property above, we have $$\partial_J(f_1(x))=f_0(\partial_G(x))=f_0(0)=0.$$ $\blacksquare$
Remember, zero is also a cycle...
So, not only the restriction makes sense but also the values of this new function lie in $Z_1(J)$. We use $f_1$ again for this new function. We have the following.
Corollary. The map of cycles $f_1:Z_1(G)\to Z_1(J)$ is well-defined.
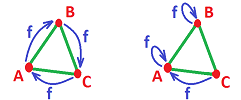
Example. Consider the graph in the form of a triangle: $$N_G=N_J=\{A,B,C\},\ E_G=E_J=\{AB,BC,CA\};$$ and suppose $f$ is this rotation: $$f_N(A)=B, \ f_N(B)=C, \ f_N(C)=A.$$ Its realization is on the left:
A quick computation shows that $$Z_1(G)=Z_1(J)=< AB+BC+CA >.$$ Now, $$\begin{array}{lll} f_1(AB+BC+CA)&=f_1(AB)+f_1(BC)+f_1(CA)\\ &=BC+CA+AB=AB+BC+CA. \end{array}$$ So, $f_1:Z_1(G)\to Z_1(J)$ is the identity (even though $f$ isn't). Conclusion: the hole is preserved.
Now, the other realization is that of the collapse of the triangle onto one of its edges given by: $$f_N(A)=A, \ f_N(B)=B, \ f_N(C)=A.$$ Then $$\begin{array}{lll} f_1(AB+BC+CA)&=f_1(AB)+f_1(BC)+f_1(CA)\\ &=AB+BA+0=0. \end{array}$$ So, the map is zero. Conclusion: the hole collapses.
$\square$
Exercise. Carry out the “quick computation”.
Exercise. Modify the computations for another rotation and another collapse.
Next, the components. This is more complicated because the $0$th homology groups of $G$ and $J$ are both quotients. We already have a homomorphism $$f_0 : C_0(G) \to C_0(J),$$ with the commutativity property, and we need to define somehow another homomorphism $$?: H_0(G) = \frac{C_0(G)}{ B_0(G)} \to H_0(J) = \frac{ C_0(J)}{ B_0(J)}.$$ The challenge is that a map on homology groups would have to handle classes of chains. The good news is that the problem is fully resolved in group theory (and in linear algebra). We review quotient maps next.
Quotient maps in algebra
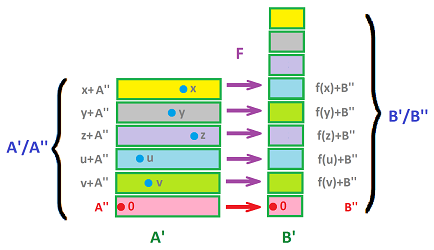
Suppose we have two groups $A, B$, and pairs of their subgroups $$A' '\subset A' \subset A, B' '\subset B' \subset B.$$ Suppose also that there is a homomorphism $$F: A \to B.$$ Then the only way to define the quotient map $$[F] : A'/A' ' \to B'/B' '$$ of $F$ is by setting its value for each equivalence class $[x]$ of $x$ to be the equivalence class of $F(x)$: $$[F]([x]) := [F(x)], \ \forall x\in A'.$$ But is this function well-defined?
What can possibly go wrong here?
First, what if $F(x) \not\in B'$? We have to require:
- (1) $F(A') \subset B'.$
Second, the formula might produce a different result if we choose another representative of the equivalence class $[x]$ of $x$. We want to ensure that this doesn’t happen: $$[y] = [x] \Rightarrow [F]([y])=[F]([x]),$$ or $$y \sim x \Rightarrow F(y) \sim F(x).$$
Recall the definition of the quotient group modulo $X$: $$a\sim b \text{ mod}(X) \Leftrightarrow a-b\in X.$$ So, we want to ensure that $$x-y\in A' ' \Rightarrow F(x)-F(y)\in B' ',$$ or $$x-y\in A' ' \Rightarrow F(x-y)\in B' '.$$ So, it suffices to ask for
- (2) $F(A' ') \subset B' '.$
This condition isn't surprising. After all, the new homomorphism should take the zero of the first quotient group, which is $A' '=0\in A' / A' '$, to the zero of the second quotient, which is $B' '=0\in B' / B' '$. The idea is illustrated below:
Example. To illustrate condition (2), consider linear operators $f:{\bf R} \to {\bf R}^3$. Which of them have well-defined quotient operator with respect to ${\bf R}^3 / {\bf R}^2$?
These are the equivalence classes:
The reflections do, but the rotations do not, unless the axis of rotation is the $z$-axis.
$\square$
Exercise. What about the stretches?
To summarize, the quotient map is well-defined provided the conditions (1) and (2) are satisfied. These two conditions can be conveniently stated as, $F$ is a map of pairs: $$F:(A',A' ')\to (B',B' ').$$
Exercise. Find all homomorphisms $f:{\bf Z}_2 \oplus {\bf Z}_2 \to {\bf Z}_2 \oplus {\bf Z}_2$ such that their quotient maps, $$[f]:\left( {\bf Z}_2 \oplus {\bf Z}_2 \right) / <(1,1)> \to \left( {\bf Z}_2 \oplus {\bf Z}_2 \right) / <(1,0)>,$$ are well-defined.
Exercise. Do the same for homomorphisms $f$ of integers and their quotients: $$[f]:{\bf Z}/<n> \to {\bf Z} /<m>.$$
Homology maps
As we examine the two requirements in the last subsection in our particular situation, we realize that for graphs we only need the latter: $$f_0(B_0(G)) \subset B_0(J).$$
Theorem. $f_0$ takes boundaries to boundaries.
Proof. Suppose $x=\partial _G(y)$, then by the commutativity formula above, we have $$f_0(x)=f_0(\partial_G(y))=\partial_J(f_1(y)).$$ $\blacksquare$
Recall that $[A]$ stands for the homology class of vertex (or a $0$-cycle) $A$ that consists of all $0$-cycles homologous to $A$.
Corollary. The map of components $[f_0]:H_0(G)\to H_0(J)$ given by $$[f_0]([A])=[f_0(A)]$$ is well-defined.
Proof. If $x\in B_0(G)$ then $f_0(x)\in B_0(J)$. Therefore, $f_0(B_0(G))\subset B_0(J)$. Further, $$[f_0]([A])=[f_0](A+B_0(G))= [f_0](A)+B_0(J)=[f_0(A)].$$ $\blacksquare$
Example. Consider this two-node graph and this single-edge graph: $$N_G=N_J=\{A,B\},\ E_G=\emptyset, \ E_J=\{AB\},$$ Merging of components is easy to illustrate with this map between them: $$f_N(A)=A,f_N(B)=B.$$ This is its realization:
It follows that $$\begin{array}{lllll} C_0(G)=H_0(G)=< [A],[B] >,\\ C_0(J)= < A,B >,H_0(J)=\{[A]=[B]\},\\ f_0([A])=f_0([B])=[A]. \end{array}$$ $\square$
Definition. The pair $f_*:=\{ [f_0],f_1 \}$ is called the homology map of the graph map $f$.
Exercise. Find the matrices of the homology map of a graph map that folds in half a graph of $2n$ edges arranged in (a) a string, (b) a circle, (c) a figure eight.
Exercise. Devise a graph map that "splits a hole" and then conduct a homological analysis to confirm this.
The following three theorems give us the main features of homology theory.
Theorem. Transitioning to homology maps preserves the identity: $$[({\rm Id}_G)_0]={\rm Id}_{H_0(G)},({\rm Id}_G)_1={\rm Id}_{H_1(G)}.$$
Theorem. Transitioning to homology maps preserves the compositions: $$[(fg)_{0}]=[f_{0}][g_{0}],(fg)_{1}=f_{1}g_{1}.$$
Theorem. Transitioning to homology maps preserves the inverses: $$[(f^{-1})_{0}]=[f_{0}]^{-1},(f^{-1})_{1}=f_{1}^{-1}.$$
Exercise. Prove these three theorems.
Example (self-maps of circle). Let's try to classify, best we can, the continuous functions of circle to circle. The best we can do, for now, is to think of the circles as realizations of two circular graphs $G,J$ made of $n,m$ nodes and $n,m$ edges respectively: $$\begin{array}{lll} N_G=\{A_0,A_1, ...,A_n=A_0\},&N_J=\{B_0,B_1, ...,B_m=B_0\}, \\ E_G=\{A_0A_1,...,A_{n-1}A_n\},&E_J=\{B_0B_1,...,B_{m-1}B_m\}, \end{array}$$ and then classify the graph maps $f:G\to J$. We have to allow all possible values of $n \ge m$ in order to be able to reproduce multiple wraps; one needs $n=2m$ for a double wrap.
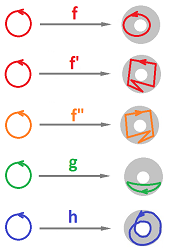
The outcome we might hope for is the one that captures the difference between a loop that goes around $1$ time from the one that goes around $2$ times from the one that goes around $3$ times, etc., and from those that go in the opposite direction:
For these functions, the numbers of turns are: $1,1,-1,0,2$. However, homology theory as it has been so far developed produces results that fall short of our goal.
The homology groups of the graphs are very simple: $$\begin{array}{lll} H_0(G)=< [A_0] >, & H_0(J)=< [B_0] >, \\ H_1(G)=< A_0A_1+ ...+A_{n-1}A_n >, & H_1(J)=< B_0B_1+...+B_{m-1}B_m >. \end{array}$$ We care only about the $1$st homology groups. Both of these groups are isomorphic to ${\bf Z}_2$; therefore, there can be only two possible homology maps: the zero and the isomorphism. In the former case, the graph map doesn't make a full turn or makes an even number of turns and in the latter case, it makes an odd number of turns, clockwise or counterclockwise. In binary arithmetic, the numbers of turns for the above functions become: $1,1,1,0,0$.
To be able to count the turns, we'd have to use directed edges and the integer arithmetic. This development is presented in the later chapters.
$\square$
Exercise. Provide the missing details: compute the homology groups of the graphs, represent the depicted functions as realizations of graph maps, compute their homology maps, etc.