Homology of balls and spheres

Redirect to:

• Cell complexes#Homology in dimension n

Let's compute the homology of the $n$-ball ${\bf B}^n$ and the $(n-1)$-sphere ${\bf S}^{n-1}, n>2$.

First, the ball.

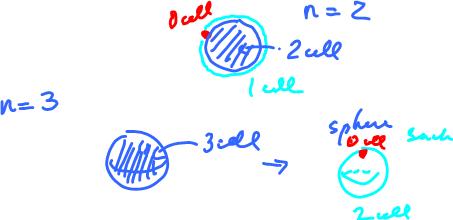
First represent ${\bf B}^n$ as a cell complex.

Cells:

• $n$-cells: ${\sigma}$,
• $(n-1)$-cells: $a$,
• $0$-cells: $A$.

The boundary operator:

• ${\partial}{\sigma} = a,$
• ${\partial}a = 0,$
• ${\partial}A = 0.$

Chain complex: $$C_{n+1}(K) \stackrel{\partial}{\rightarrow} C_n(K) \stackrel{\partial}{\rightarrow} C_{n-1}(K) \stackrel{\partial}{\rightarrow} C_{n-2}(K) \stackrel{\partial}{\rightarrow} ... C_1(K) \stackrel{\partial}{\rightarrow} C_0(K)$$

$$\begin{array}{llllll} 0 \stackrel{0}{\rightarrow} &{\rm span \hspace{3pt}}{\sigma} &\stackrel{\rm iso}{\rightarrow} &{\rm span \hspace{3pt}}{a} &\stackrel{0}{\rightarrow} &0 &\stackrel{0}{\rightarrow} &... &0 \stackrel{0}{\rightarrow} &{\rm {\rm span \hspace{3pt}}}{A} &{\rightarrow} &0 \\ &{\sigma} &{\rightarrow} &a &{\rightarrow} &0 & & & &A &{\rightarrow} &0. \\ {\rm kernels:} &Z_n = 0 & & Z_{n-1} = {\rm span \hspace{3pt}}{a} & & Z_{n-2} = 0 & &... &Z_1 = 0 & &Z_0 = {\rm span \hspace{3pt}}{A} \\ {\rm images:} &B_n = 0 & & B_{n-1} = {\rm span \hspace{3pt}}{a} & & B_{n-2} = 0 & &... &B_1 = 0 & & B_0 = 0 \\ {\rm quotients:} &H_n = 0 & & H_{n-1} = 0 & & H_{n-2} = 0 & & ... &H_1 = 0 & & H_0 = {\rm span \hspace{3pt}}{A} \end{array}$$

Here: "iso" = "isomorphism", kernels of what's on the right, images of what's on the left.

Next the sphere.

The sphere ${\bf S}^{n-1}$ has the same cell complex except for the $n$-cell which is missing.

Cells:

• $(n-1)$-cells: $a$,
• $0$-cells: $A$.

The boundary operator:

• ${\partial}a = 0,$
• ${\partial}A = 0.$

Chain complex: $$\begin{array}{llllll} C_{n+1}(K) &\stackrel{\partial}{\rightarrow} &C_n(K) &\stackrel{\partial}{\rightarrow} &C_{n-1}(K) &\stackrel{\partial}{\rightarrow} &C_{n-2}(K) &\stackrel{\partial}{\rightarrow} &... &C_1(K) &\stackrel{\partial}{\rightarrow} &C_0(K) \\ 0 &\stackrel{0}{\rightarrow} &0 &\stackrel{0}{\rightarrow} &{\rm span \hspace{3pt}}{a} &\stackrel{0}{\rightarrow} &0 &\stackrel{0}{\rightarrow} &... &0 &\stackrel{0}{\rightarrow} &{\rm span}{A} &{\rightarrow} 0 \\ & & & &a &{\rightarrow} &0 & & & & & A &{\rightarrow} 0. \\ {\rm kernels:} & &Z_n = 0 & & Z_{n-1} = {\rm span}{a} & & Z_{n-2} = 0 & & ... &Z_1 = 0 & &Z_0 = {\rm span}{A} \\ {\rm images:} & &B_n = 0 & & B_{n-1} = 0 & & B_{n-2} = 0 & & ... &B_1 = 0 & &B_0 = 0 \\ {\rm quotients:}& &H_n = 0 & & H_{n-1} = {\rm span}{a} & & H_{n-2} = 0 & & ... &H_1 = 0 & &H_0 = {\rm span}{A} \end{array}$$

To summarize...

Theorem.

• $H_k({\bf B}^n) = 0$ for $k \neq 0$, $H_k({\bf B}^n) = {\bf R}, n = 0, 1, 2, ...$
• $H_k({\bf S}^n) = 0$ for $k \neq 0,n, H_0({\bf S}^n) = H_n({\bf S}^n) = {\bf R}, n = 2, 3, ...$

Exercise. Solve the problem for $n = 1, 2$.