Graph representation of topology of color images

Start at Graph representation of topology of gray scale images and Color images.

What is the topology of a color image?

The RGB color space is $$C = \{ (r, g, b) : 0 ≤ r, g, b ≤ 255 \}.$$ There is a natural partial order on $C$: $$r ≤ r’, g ≤ g’, b ≤ b’ \Rightarrow (r, g, b) ≤ (r’, g’, b’).$$

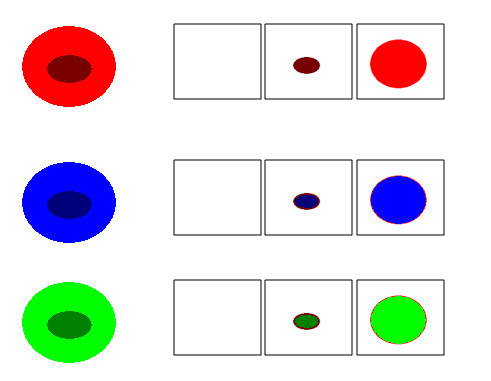
If only one of the three primary color is changing, the topology is the same as that of the corresponding gray scale image:

Then we recognize objects as darker areas surrounded by lighter background. Similarly, all three colors may be changing producing the same effect of a dark object on a light background. The rule applies to more general situations.

To make this specific, suppose we have a color image as a function $J:[0,N] \times [0,M] → C$, where $C$ is the RGB color space.

If we have any function $P:C → [0,255]$, then the composition $PJ:[0,N] \times [0,M] → [0,255]$ is a gray scale image. Suppose also that $P$ is increasing with respect to the partial order: $$r≤r', g≤g', b≤b' \Rightarrow P(r,g,b)≤P(r',g',b').$$ What this means is that the darker/lighter relationship between pixels is preserved under $P$ but some of it may disappear. In other words, the gray scale of $PJ$ is becoming darker as the color of $J$ is becoming darker.

Two things follow:

1. Every darker area surrounded by a lighter background in the gray scale image $PJ$ appears as a darker area surrounded by a lighter background in the original image $J$, for any $P$.
2. Every darker area surrounded by a lighter background in image $J$ appears as a darker area surrounded by a lighter background in the gray scale image $PJ$, for some $P$.

Therefore, in order to capture the topology of $J$ one needs to capture the topologies of all possible gray scale images $PJ$, without double counting.

A similar analysis will lead to an even simpler conclusion that in order to capture the topology of $J$ one needs to captures the topologies of all of its possible binarizations (via thresholding), without double counting.

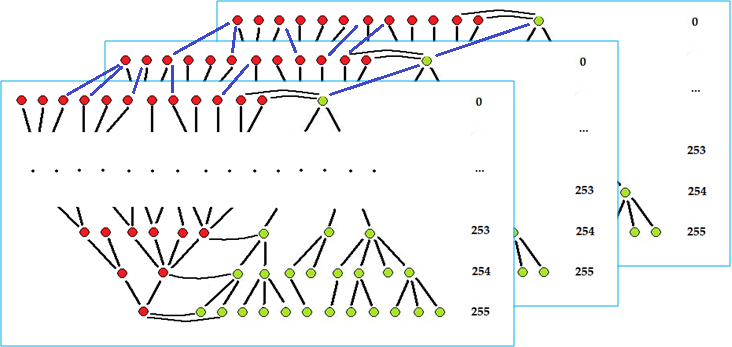
Topology graph of a color image

The nodes of the topology graph are the objects and holes in the thresholded image and there is an arrow from node $A$ to node $B$ if:

• object $B$ has hole $A$, provided $A$ and $B$ correspond to consecutive colors.
• object $B$ has hole $A$, provided $A$ and $B$ correspond to the same color.
• And vice versa.

Each of these slices is the topology graph of the gray scale image obtained from the color image by fixing a value of, say, green and blue and letting red vary. The end result is a box filled with graphs connected with its neighbors.

How to build the topology graph

All pixels in the image are ordered according to the partial order.

• Following this order, each pixel is processed:
  • add its vertices, unless those are already present as parts of other pixels;
  • add its edges, unless those are already present as parts of other pixels;
  • add the face of the pixel.
• At every step, the graph is given a new node and arrows that connect the nodes in order to represent the merging and the splitting of the cycles:
  • adding a new vertex creates a new component;
  • adding a new edge may connect two components, or create, or split a hole;
  • adding the face to the hole eliminates the hole.

For how, see Adding pixels.

Complete analysis

• Same as for gray scale but based on the partial order above
• Threshold the image to create $256 \times 256 \times 256$ binary images.
• Collect all objects and holes in the topology graph, as above.
• Filter noise out if necessary.
• Choose the tips, etc to give the "binary" topology of the image.