Euler characteristic of surfaces

Redirect to:

• Euler characteristic

The Euler characteristic $\chi(K)$ of $n$-dimensional cell complex $K$ is defined as the alternating sum of the number of cells in $K$ for each dimension:

$\chi(K) = \# 0$-cells $- \# 1$-cells $+ \# 2$-cells $- ... \pm \# n$-cells.

In case of surfaces, this is simply: $$\begin{array}{} \chi(K) &= \# 0{\rm -cells \hspace{3pt}} - \# 1{\rm -cells \hspace{3pt}} + \# 2{\rm -cells \hspace{3pt}} \\ &= \# {\rm \hspace{3pt} vertices} - \# {\rm \hspace{3pt} edges} + \# {\rm \hspace{3pt} faces}. \end{array}$$

Exercise. Compute the Euler characteristic of

• the Klein bottle,
• the $n$-torus.

Theorem. The Euler characteristic is a topological invariant, i.e., if surfaces $S$ and $T$ are homeomorphic, then $\chi(S) = \chi(T)$.

The converse of this theorem is not true, i.e., the Euler characteristic is not a complete topological invariant. Indeed there are non-homeomorphic complexes with the same Euler characteristic. Find examples (Exercise).

To justify this theorem, consider what elementary subdivisions of a $2$-dimensional cell complex do to the Euler characteristic:

Exercise. Show that if $S'$ is the barycentric subdivision of $S$ then $$\chi(S') = \chi(S).$$

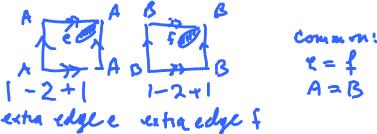
Let's consider what happens to the Euler characteristic when we form the connected sum of two tori.

Cutting the disks out has the following consequences:

• no new faces, net effect $0$,
• one new, shared edge, net effect $-1$,
• one existing vertex becomes shared, net effect $-1$.

Thus, the net effect is $-2$.

This argument applies to all surfaces:

Theorem. For two surfaces $S$ and $T$, $$\chi(S \# T) = \chi(S) + \chi(T) - 2.$$

Exercise. Use the formula to compute the Euler characteristic of the $n$-torus.

For more see also Euler-Poincare formula.