This site is being phased out.
Euler characteristic of graphs
Redirect to:
Euler characteristic
The Euler characteristic of graph $G$ is simply $$\chi(G) = \# \text{ of vertices } - \# \text{ of edges}.$$
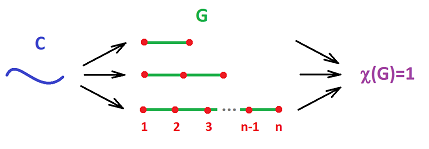
The topological significance of this number becomes clear if we consider a simple path $C$ in space. It can be a realization of a various graphs $G$ but suppose $G$ is a sequence of $n$ consecutive edges:
Then $$\chi (G) = n-(n-1)=1.$$ So, the number is independent from $n$! Therefore, it can be an attribute (characteristic!) of the path itself that separates it from all other curves. To make this conclusion, however, we need the following
Theorem. If a simple path is a realization of a graph, then this graph is a sequence of $n\ge 1$ consecutive edges.
Exercise. Prove the theorem.
Exercise. Show that if $C$ consists of $k$ path-components each of which is a simple curve and $C=|G|$ then $\chi (G) =k$.
So, maybe $\chi (G)$ is the number of path components of $|G|$? The example of a triangle $T$ shows that this is not correct as $\chi (T) = 0$. Below is best we can do.
Theorem. If $T$ is a tree (i.e., a connected graph with no cycles) then $$\chi(T) = 1.$$
Proof. Idea: Remove an edge then use induction.
So, we use induction on the number of edges the graph.
First, tree $T$ with a single edge has $\chi(T) = 1.$ Now, we assume that any tree with fewer than $n$ edges satisfies this equation. Suppose that tree $T$ has $n$ edges.
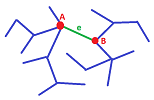
Remove any edge, $e=AB$, from $T$. The result is a new graph $G$ and $E_G=E_T - \{e \}$.
What kind of graph is it?
It is disconnected. Indeed, let $H=[A],K=[B]$, the components of $A,B$ respectively. As we know, each is connected. Secondly, removing an edge can't create cycles (Exercise...), so both are trees. Thirdly, there is no path from $A$ to $B$, because if there was one, say, $P$, then the combination of $P$ and $e$ would be a path from $A$ to $A$, a cycle in the tree $T$. Therefore, $H$ and $K$ are disjoint. Fourthly, Exercise...
So, $G$ splits into two trees $H$ and $K$ and each has fewer than $n$ edges. Therefore, by assumption $$\chi(H) = \chi(K) = 1.$$
Let's compute now: $$\begin{array}{llllll} \chi(T) & =&&\# \text{ of vertices of } T - \# \text{ of edges of } T\\ & =&&\# \text{ of vertices of } G - ( \# \text{ of edges of } G + 1) \\ & =&&\# \text{ of vertices of } G - \# \text{ of edges of } G - 1 \\ & =&& \binom {\# \text{ of vertices of } H} {+ \# \text{ of vertices of } K} - \binom {\# \text{ of edges of } H} {+ \# \text{ of edges of } K} -1\\ & =&&\big( \# \text{ of vertices of } H - \# \text{ of edges of } H \big)\\ & &+&\big(\# \text{ of vertices of } K - \# \text{ of edges of } K \big) - 1\\ & =&&\chi(H) \\ & &+&\chi(K) -1\\ &=&&1+1-1\\ &=&&1. \end{array}$$
$\blacksquare$
Exercise. Repeat the proof of the theorem for $e$ an “end-edge”.
Exercise. What about the converse?
Corollary. If $G$ consists of $n$ disjoint trees, then $\chi (G) =n$.
Exercise. Prove it.
Exercise. Prove this generalization of the above theorem:
Theorem. If $G$ is a graph, then $$\chi(T) \le 1.$$ Moreover, $\chi(G) = 1$ if and only if $G$ is a tree.
Holes of planar graphs
What is a hole in the graph?
First, a tree has no holes! On the other hand, it has no cycles. We have a match here.
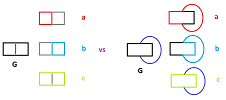
In general, we can't say what a hole is. Even though we can count holes -- as the number of linearly independent cycles -- we can't point at one of them and say “That's a hole and the rest aren't”. The example below shows that which of the cycles “naturally” look like holes depends on the realization of the graph:
Indeed,
- 1. for the first realization the holes “are” cycles $a$ (red) and $b$ (blue) but not $c$ (green); while
- 2. for the second realization, it's $b$ and $c$.
This topological ambiguity is, in fact, a good news because it is fully matched by the algebraic ambiguity. Indeed, in $C_1=\{0,a,b,c=a+b\}$, then
- 1. $a$ and $b$ are generators but
- 2. so are $b$ and $c$!
(In the language of linear algebra, these are two bases of this vector space.)
We still would like to confirm our intuition about what holes in a graph are. For that we will limit our attention to a simpler kind -- planar graphs.
Suppose graph $G$ is realized in the plane:
The idea is, once a realization $|G|$ of $G$ is chosen, the holes become visible as path-components of the complement of $|G|$.
Sidenote: This is an instance of the Alexander duality. $\square$
We rely on the following two theorems.
Jordan theorem. The complement of a simple closed curve in the plane has two path-connected components (one bounded and one unbounded).
Theorem. If a simple closed curve is a realization of a graph, then this graph is a cycle of $n\ge 1$ consecutive edges.
Exercise. Prove the theorem. Hint: Try to answer these questions about $G$: how many components? cycles? holes? forks? end-points?
So, we have a one-to-one correspondence between:
- path-components of ${\bf R}^2 - |G|$,
- the loops in $G$ that bound them, and
- a certain basis of the space of cycles in $G$.
Let's count holes in this environment now.
Suppose we are given a connected planar graph $G$ with a specific realization $|G|$ in the plane. The idea is to remove some edges one by one until we have a tree.
The process is inductive. We start with our graph $G=G_0$. Then at each step $k$ we pick an edge in graph $G_k,k=0,1,...,$ that is a part of a cycle that bounds a hole in $G_k$ and remove it from the graph. This creates a new graph $G_{k+1}$. Of course, removing an edge in a cycle that surrounds a hole “kills” the hole by merging it with another or with the outside. Then $$\# \text{ of holes in } |G_{k+1}| = \# \text{ of holes in } |G_k| -1.$$ $$\# \text{ of edges in } G_{k+1} = \# \text{ of edges in } G_k -1.$$ We claim that after every step the new graph is connected (Exercise...).
Theorem. If a plane realization $|G|$ of a connected graph $G$ has $n$ holes then $$\chi(G) = 1 - n.$$
Proof. Above, we have shown that the graph with $n$ holes will need $n$ edges removed to turn it into a tree. Then the last theorem applies. $\blacksquare$
More importantly, we have the following
Corollary. For any connected planar graph $G$, $$\# \text{ of holes of } |G|= 1 - \chi(G).$$
So, since the number on the right is independent from a choice of realization, so it the number on the left. This confirms the results of our algebraic analysis of cycles presented above.
While useful, this non-algebraic approach is a poor-man's solution of this problem.
Exercise. What if $G$ isn't connected?
Euler formula
The Euler characteristic of a polyhedron $P$ is defined as $$\chi (P) =\# \text{ of vertices } -\# \text{ of edges } +\# \text{ of faces }.$$
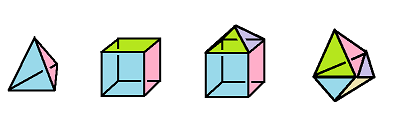
It was noticed by Euler that $$\chi (P) =2$$ for any convex polyhedron:
We would like to use the last theorem to confirm this observation.
It is clear that the collection of vertices and edges of polyhedron $P$ is always a realization of some graph $G_P$, but is it planar?
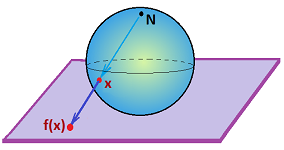
It is, under an appropriate choice of stereographic projection:
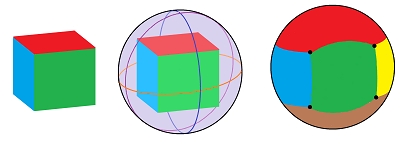
However, it is more meaningful to realize them on the sphere -- via the radial projection (Exercise...) -- such as this cube:
Then, the above results remain valid except that all components of the complement are bounded and we have to take that into account: $$\begin{array}{lllllll} \chi(P) & \\ =\# \text{ of vertices of } P-\# \text{ of edges of } P +\# \text{ of faces of } P \\ =\# \text{ of vertices of } G_P-\# \text{ of edges of } G_P +(\# \text{ of holes of } G_P +1)\\ =\chi(G_P) +\# \text{ of holes of } G_P +1\\ =\chi(G_P) +(1-\chi(G_P)) +1\\ =1+1\\ =2. \end{array}$$ This is called the Euler formula.
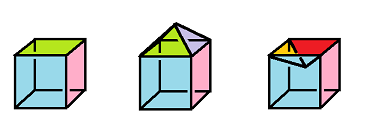
We can also observe that adding a sloped roof to a cube or making an indentation produce the same effect on the number of vertices and edges and it preserves the Euler characteristic:
Exercise. Prove that.
But the former is convex while the latter isn't! This suggests that the Euler characteristic has nothing to do with convexity and may depend only on the topology of the polyhedron.
Exercise. Try the torus.
Exercise. Suppose graph $G$ is the disjoint union of $m$ trees, find its Euler characteristic.
Exercise. Suppose graph $G$ has $m$ components and $n$ holes, find its Euler characteristic.
An alternative approach to the proof is outlined below.
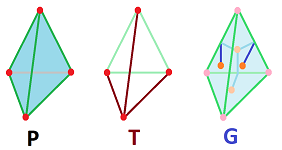
We assume that $P$ is a polyhedron that satisfies:
- $P$ is path-connected;
- Every loop cuts $P$ into two disjoint pieces.
The idea of the proof is to build two graphs on $P$ with the following properties:
- graph $T$ captures all vertices of $P$ and some edges;
- graph $G$ captures all faces of $P$ and the rest of the edges.
Now, this what we know about graphs: $$V_T-E_T=1,$$ $$V_{G}-E_{G}=1.$$ Add the equations and re-arrange: $$V_T-(E_T+E_G)+V_G=2.$$ An examination reveals that these three terms are:
of $P$. And the theorem follows.
We just need to build $T$ and $G$ satisfying the conditions. We rely on the following result.
Exercise. Prove that every graph has a subgraph which
- contains all of the original vertices, and
- is a tree.
We apply this result to the $1$-skeleton of $P$. Then, we have its subgraph $T$ which is a tree and
Next, the idea of $G$ is that of the "dual graph" of $T$:
- $G$'s vertices are the middle points of the faces.
- $G$'s edges connect $G$'s vertices by crossing the edges of $P$, but not the edges of $T$.
Exercise. It is always possible to get from one face to any adjacent face without crossing $T$. Why?