This site is being phased out.
Elementary Linear Algebra -- Spring 2018 -- midterm
MATH 329 -- Spring 2018 -- midterm exam
Name:_________________________ $\qquad$ 8 problems, 10 points each
- Write the problems in the given order, each problem on a separate page.
- Show enough work to justify your answers.
$\bullet$ 1. Set up, but do not solve, a system of linear equations for the following problem: “Suppose your portfolio is worth $\$ 1,000,000$ and it consists of two stocks $A$ and $B$. The stocks are priced as follows: $A$ $\$2.1$ per share, $B$ $\$1.5$ per share. Suppose also that you have twice as much of stock $A$ than $B$. How much of each do you have?”
$\bullet$ 2. In an effort to find the line in which the planes $ 2x -y- z=2 $ and $-4x+2y+2z=1$ intersect, a student multiplied the first one by $2$ and then added the result to the second. He got $0=5$. Explain the result.
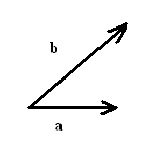
$\bullet$ 3. Vectors $A$ and $B$ are given below. Copy the picture and illustrate graphically: (a) $A+B$, (b) $A-B$, (c) $||A||$, (d) the projection of $A$ on $B$, (e) the projection of $B$ on $A$.
$\bullet$ 4. Find the angle between the vectors $<1,1,1>$ and $<1,0,0>$. Don't simplify.
$\bullet$ 5. Find the vector equation of the line parallel to both $xy$- and $xz$- coordinate planes and passing through $(2,3,1)$.
$\bullet$ 6. Solve the system of linear equations: $$\left\{\begin{array}{lll} x&-y&=-1,\\ 2x&+y&=0.\\ \end{array}\right.$$
$\bullet$ 7. Is it possible that a system of linear equations has (a) no solutions, (b) one solution, (c) two solutions, (d) infinitely many solutions? Give an example or explain why it's not possible.
$\bullet$ 8. Represent the system of linear equations as a matrix equation: $$\left\{\begin{array}{lll} x&-y&+z&=-1,\\ 3x&&+z&=2,\\ 2x&+y&+z&=1. \end{array}\right.$$